|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Поиск на графе
Анализ алгоритмов на графах
Мы уже можем рассмотреть широкий набор задач обработки графов и методов их решения, чтобы в дальнейшем не всегда сравнивать различные многочисленные алгоритмы решения одной и той же задачи. Хотя всегда полезно набраться опыта работы с алгоритмами, проверяя их на реальных данных или же на сгенерированных данных, которые понятны нам и обладают теми же свойствами, что и реальные данные.
Как было кратко отмечено в "Принципы анализа алгоритмов" , мы стремимся (в идеальном случае) получить естественные модели входных данных, обладающие тремя важными свойствами:
- Они достаточно точно соответствуют реальным данным, чтобы использовать их для прогнозирования производительности.
- Они достаточно просты, чтобы подвергнуть их математическому анализу.
- Можно написать генераторы экземпляров задач, которые можно использовать для тестирования наших алгоритмов.
При наличии этих трех компонентов можно приступать к циклу проектирования, анализа, реализации и тестирования, который позволяет создавать эффективные алгоритмы для решения практических задач.
В таких областях, как сортировка и поиск, подобные циклы позволили нам добиться значительных успехов в частях 3 и 4. Мы можем анализировать алгоритмы, генерировать случайные экземпляры задач и совершенствовать программные реализации, чтобы получать высокоэффективные программы для использования в самых разнообразных практических ситуациях. В ряде других областей могут возникнуть различные трудности. Например, математический анализ на приемлемом для нас уровне невозможен при решении многих геометрических задач, а разработка точной модели входных данных — серьезная проблема для многих алгоритмов обработки строк (поскольку сама такая разработка требует существенных вычислений). Вот и алгоритмы на графах приводят нас к ситуации, когда зачастую приходится балансировать между тремя вышеупомянутыми свойствами:
- Математический анализ очень труден, и поэтому многие аналитические вопросы остаются без ответа.
- Существует очень много различных видов графов, и невозможно достаточно полно протестировать наши алгоритмы на всех этих видах.
- Классификация видов графов, которые возникают в практических задачах, по большей части представляет собой плохо понимаемую задачу.
Из-за сложности графов часто не удается в полной мере оценить существенные свойства графов, с которыми приходится сталкиваться на практике, или искусственных графов, которые мы (возможно) можем генерировать и анализировать.
Вообще-то ситуация не так уж безнадежна, по одной простой причине: многие из рассматриваемых нами алгоритмов на графах оптимальны в худшем случае, и поэтому прогнозирование производительности алгоритмов не представляет трудностей. Например, программа 18.7 находит мосты, просмотрев лишь один раз каждое ребро и каждую вершину. Эти затраты совпадают с затратами на построение структуры данных графа, и мы можем уверенно предсказать, например, что удвоение количества ребер приведет к удвоению времени выполнения, независимо от вида обрабатываемых графов.
Однако если время выполнения алгоритма зависит от структуры входного графа, прогнозы становятся не таким простым делом. Но если понадобится обработать очень много больших графов, то нам нужны эффективные алгоритмы по той же причине, по какой они требуются и в любой другой проблемной области. Поэтому мы продолжим изучение основных свойств алгоритмов и их применений и постараемся выявить методы, наиболее удобные для обработки графов, которые могут встретиться на практике.
Для иллюстрации некоторых из этих вопросов мы вернемся к изучению свойства связности графа — т.е. к задаче, которую мы начали рассматривать еще в главе 1 "Введение" . Связность случайных графов привлекала к себе внимание математиков в течение многих лет, и данной теме посвящена обширная литература. Эта литература выходит за рамки настоящей книги, однако она представляет собой фон, который оправдывает использование этой задачи как основы для некоторых экспериментальных исследований, углубляющих наше понимание базовых алгоритмов и изучаемых видов графов.
Например, постепенное построение графов добавлением случайных ребер во множество первоначально изолированных вершин (по существу, этот процесс выполняется в программе 19.12) представляет собой хорошо изученный процесс, лежащий в основе классической теории случайных графов. Известно, что при возрастании количества ребер такой граф сливается в один гигантский компонент. Литература по случайным графам дает обширную информацию о природе этого процесса. Например:
Лемма 18.13. Если  (при положительном
(при положительном 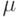 ), то случайный граф с V вершинами и E ребрами состоит из одного связного компонента и изолированных вершин, среднее количество которых не превышает
), то случайный граф с V вершинами и E ребрами состоит из одного связного компонента и изолированных вершин, среднее количество которых не превышает  , с вероятностью, приближающейся к 1 при бесконечном возрастании V.
, с вероятностью, приближающейся к 1 при бесконечном возрастании V.
Доказательство. Этот факт был установлен в пионерской работе Эрдеша (Erdos) и Реньи (Renyi) в 1960 г. Само доказательство выходит за рамки данной книги (см. раздел ссылок). 
На основании этой леммы можно ожидать, что крупные неразреженные случайные
графы являются связными. Например, если V> 1000 и E > 10V, то 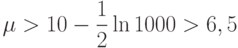 , и среднее количество вершин, не содержащихся в гигантском компоненте, (почти наверняка) меньше, чем
, и среднее количество вершин, не содержащихся в гигантском компоненте, (почти наверняка) меньше, чем  . Если сгенерировать миллион случайных графов с 1000 вершинами и плотностью, большей 10, то среди них могут оказаться несколько графов с одной изолированной вершиной, но остальные графы будут связными.
. Если сгенерировать миллион случайных графов с 1000 вершинами и плотностью, большей 10, то среди них могут оказаться несколько графов с одной изолированной вершиной, но остальные графы будут связными.
На рис. 18.30 обычные случайные графы сравниваются со случайными графами с соседними связями, в которых разрешены лишь ребра, соединяющие только такие вершины, индексы которых различаются не более чем на некоторую небольшую константу. Модель графа с соседними связями порождает графы, которые по своим характеристикам существенно отличаются от случайных графов. В конечном итоге мы все-таки получим гигантский компонент, но он появится внезапно, при слиянии двух крупных компонентов.
Из таблицы 18.1 видно, что эти структурные различия между случайными графами и графами с соседними связями сохраняются и тогда, когда V и E находятся в пределах, представляющих практический интерес. Конечно, такие структурные различия могут отразиться на производительности алгоритмов.
Здесь показаны 10 этапов эволюции двух видов случайных графов при добавлении 2E ребер в первоначально пустые графы. Каждый график представляет собой гистограмму количества вершин в компонентах размером от 1 до V— 1 (слева направо). Вначале все вершины содержатся в компонентах размером 1, а в конце практически все вершины входят в один гигантский компонент. Графики слева соответствуют обычному случайному графу: гигантский компонент формируется быстро, а все другие компоненты малы. Графики справа соответствуют случайному графу с соседними связями: компоненты различных размеров сохраняются в течение более длительного времени.
| E | Случайные ребра | Случайные ребра из 10 соседних | ||
|---|---|---|---|---|
| C | L | C | L | |
| 1000 | 99000 | 5 | 99003 | 3 |
| 2000 | 98000 | 4 | 98010 | 4 |
| 5000 | 95000 | 6 | 95075 | 5 |
| 10000 | 90000 | 8 | 90300 | 7 |
| 20000 | 80002 | 16 | 81381 | 9 |
| 50000 | 50003 | 1701 | 57986 | 27 |
| 100000 | 16236 | 79633 | 28721 | 151 |
| 200000 | 1887 | 98049 | 3818 | 6797 |
| 500000 | 4 | 99997 | 19 | 99979 |
| 1000000 | 1 | 100000 | 1 | 100000 |
В этой таблице показано количество связных компонентов и размер максимального связного компонента в графах, содержащих 100 000 вершин и полученных из двух различных распределений. Для модели случайного графа эксперименты подтверждают известный факт, что если среднее значение степени вершин превышает некоторую небольшую константу, то граф с высокой вероятностью состоит в основном из одного гигантского компонента. В двух правых столбцах приведены экспериментальные данные при наличии ограничения: ребра могут соединять каждую вершину лишь с одной из 10 указанных соседних вершин.
В таблицу 18.2 сведены эмпирические значения затрат на определение количества связных компонентов случайного графа с помощью различных алгоритмов. Прямое сравнение этих алгоритмов не вполне уместно, поскольку они разрабатывались для решения различных задач, однако эксперименты все же подтверждают некоторые наши выводы.
Во-первых, из таблицы ясно, что не следует использовать представление матрицей смежности для больших разреженных графов (и невозможно для очень больших) — не только из-за неподъемных затрат на инициализацию матрицы, но и потому, что алгоритм просматривает каждый элемент матрицы, вследствие чего время его выполнения пропорционально размеру матрицы (V2), а не количеству единиц в ней (E). Например, из таблицы следует, что в случае использования матрицы смежности на обработку графа с 1000 ребрами нужно примерно столько же времени, что и на обработку графа, содержащего 100 000 ребер.
Во-вторых, из таблицы 18.2 также ясно, что затраты на выделение памяти под узлы списков смежности для крупных разреженных графов довольно велики. Затраты на построение таких списков превосходят затраты на обход более чем в пять раз. В типичной ситуации, когда после построения графа нужно выполнить много разных поисков, такая цена приемлема. Иначе лучше рассмотреть альтернативные реализации, позволяющие снизить эти затраты.
| E | U | U* | Матрица смежности | Списки смежности | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| I | D | D* | I | D | D* | B | B* | |||
| 5000 вершин | ||||||||||
| 500 | 1 | 0 | 255 | 312 | 356 | 1 | 0 | 0 | 0 | 1 |
| 1000 | 0 | 1 | 255 | 311 | 354 | 1 | 0 | 0 | 0 | 1 |
| 5000 | 1 | 2 | 258 | 312 | 353 | 2 | 2 | 1 | 2 | 1 |
| 10000 | 3 | 3 | 258 | 314 | 358 | 5 | 2 | 1 | 2 | 1 |
| 50000 | 12 | 6 | 270 | 315 | 202 | 25 | 6 | 4 | 5 | 6 |
| 100000 | 23 | 7 | 286 | 314 | 181 | 52 | 9 | 2 | 10 | 11 |
| 500000 | 117 | 5 | 478 | 248 | 111 | 267 | 54 | 16 | 56 | 47 |
| 100000 вершин | ||||||||||
| 5000 | 5 | 3 | 3 | 8 | 7 | 24 | 24 | |||
| 10000 | 4 | 5 | 6 | 7 | 7 | 24 | 24 | |||
| 50000 | 18 | 18 | 26 | 12 | 12 | 28 | 28 | |||
| 100000 | 34 | 35 | 51 | 28 | 24 | 34 | 34 | |||
| 500000 | 133 | 137 | 259 | 88 | 89 | |||||
| Обозначения: | |
| U | Взвешенное быстрое объединение со сжатием пути делением пополам (программа 1.4) |
| I | Начальное создание представления графа |
| D | Рекурсивный DFS (программа 18.3) |
| B | BFS (программа 18.9) |
| * | Выход сразу при установлении полной связности графа |
В этой таблице показаны относительные значения времени определения различными алгоритмами количества связных компонентов (и размера наибольшего из них) для графов с различным количеством вершин и ребер. Как и ожидалось, алгоритмы, которые используют представление матрицей смежности, медленно работают на разреженных графах, но вполне конкурентоспособны на насыщенных графах. В случае данной задачи алгоритмы объединения-поиска, которые были рассмотрены в "Введение" , работают быстрее всего, т.к. они строят структуру данных, предназначенную специально для решения данной задачи, а поэтому не нуждаются в другом представлении графа. Но если структура данных, представляющая граф, уже построена, то алгоритмы DFS и BFS оказываются быстрее и гибче. Добавление проверки для прекращения работы, когда уже понятно, что граф представляет собой единый связный компонент, существенно повышает быстродействие поиска в глубину и объединения-поиска (но не поиска в ширину) при обработке насыщенных графов.
В-третьих, весьма показательно отсутствие чисел в столбцах DFS для крупных разреженных графов. Такие графы заводят рекурсию в бездонную глубину, которая (в конечном итоге) приводит к аварийному завершению программы. Если мы хотим использовать поиск в глубину для таких графов, необходимо применять нерекурсивные версии программ, описанные в разделе 18.7.
В-четвертых, эта таблица показывает, что метод на основе объединения-поиска, описанный в "Введение" , работает быстрее поисков в глубину и в ширину — главным образом потому, что ему не нужно представление всего графа. Однако, не имея такого представления, мы не можем дать ответ на такие простые запросы, как " Существует ли ребро, соединяющее вершины v и w? " . Поэтому методы на основе объединения-поиска не годятся, если мы хотим получить больше, чем то, для чего они предназначены (например, ответы на запросы типа " Существует ли путь, соединяющий вершины v и w? " вперемешку с добавлением ребер). Если внутреннее представление графа уже построено, не стоит трудиться над реализацией алгоритма объединения-поиска только для того, чтобы узнать, связен граф или нет, поскольку и DFS, и BFS могут дать ответ так же быстро.
При эмпирических сравнениях для составления подобных таблиц могут потребоваться объяснения различных аномалий. Например, на многих компьютерах архитектура кэша и другие свойства системы управления памятью могут существенно повлиять на производительность алгоритма на крупных графах. Повышение производительности критических приложений может потребовать, помимо всех рассматриваемых здесь факторов, и подробного изучения архитектуры машины.
Внимательное изучение этих таблиц позволяет обнаружить больше свойств этих алгоритмов, чем мы способны рассмотреть. Однако наша цель состоит не в тщательном анализе, а в демонстрации, что несмотря на множество проблем при сравнении различных алгоритмов на графах, мы можем и должны проводить эмпирические исследования и использовать любые доступные аналитические результаты, чтобы получить представление об основных особенностях алгоритмов и прогнозировать их производительность.
Упражнения
18.72. Составьте на основе эмпирических исследований таблицу наподобие таблицы 18.2 для задачи определения, является ли граф двудольным (может ли быть раскрашен двумя красками).
18.73. Составьте на основе эмпирических исследований таблицу наподобие таблицы 18.2 для задачи определения, является ли граф двусвязным.
18.74. Определите эмпирически ожидаемый размер второго по величине связного компонента разреженных графов различных размеров, построенных на основе различных моделей (см. упражнения 17.64—17.76).
18.75. Напишите программу для построения графиков наподобие рис. 18.30 и протестируйте ее на графах различных размеров, построенных на основе различных моделей (см. упражнения 17.64—17.76).
18.76. Измените программу из упражнения 18.75, чтобы она строила аналогичные гистограммы для размеров реберно-связных компонентов.
18.77. Числа в таблицах, приведенных в данном разделе, получены при исследовании только одной выборки. Можно подготовить аналогичную таблицу, каждый элемент которой будет получен на основе 1000 экспериментов, и подсчитать среднее значение и среднеквадратичное отклонение для каждой выборки (хотя таблица станет слишком большой). Будет ли такой подход более эффективен? Обоснуйте свой ответ.

