Хеширование

Цепочки переполнения

Рассмотренные в разделе 14.1 функции хеширования преобразуют ключи в адреса таблицы; второй компонент алгоритма хеширования — определение обработки случаев, когда два ключа преобразуются в один и тот же адрес. Первое, что приходит на ум — построить для каждого адреса таблицы связный список элементов, ключи которых отображаются на этот адрес. Этот подход непосредственно приводит к обобщению метода элементарного поиска в списке (см. "Таблицы символов и деревья бинарного поиска" ) в программе 14.3, в которой вместо единственного списка используются M списков.

Такой метод традиционно называется цепочками переполнения (separate chaining), поскольку конфликтующие элементы объединяются в отдельные связные списки-цепочки. Пример таких цепочек приведен на рис. 14.6. Как и в случае элементарного последовательного поиска, эти списки можно хранить упорядоченными или оставить неупорядоченными. Здесь присутствует тот же основной компромисс, что и описанный в "Таблицы символов и деревья бинарного поиска" , но для цепочек переполнения более важна не экономия времени (поскольку списки невелики), а экономия памяти (поскольку списков много).

Для упрощения кода вставки в упорядоченный список можно было бы использовать ведущий узел, но применение M ведущих узлов для отдельных цепочек переполнения не всегда удобно.

Рис. 14.6. Хеширование с цепочками переполнения

Здесь показан результат вставки ключей A S E R C H I N G X M P L в первоначально пустую хеш-таблицу с цепочками переполнения (неупорядоченные списки); используются хеш-значения, приведенные вверху. A попадает в список 0, затем S попадает в список 2, E — в список 0 (в его начало, чтобы время вставки было постоянным), R — в список 4 и т.д.

Программа 14.3. Хеширование с цепочками переполнения

Данная реализация таблицы символов основана на замене конструктора ST и функций search и insert в таблице символов с применением связных списков из программы 12.6 на приведенные здесь функции, а также на замене ссылки head на массив ссылок heads. Здесь используются те же рекурсивные функции поиска и удаления в списке, что и в программе 12.6, но при этом используются M списков с ведущими ссылками в heads, с использованием хеш-функции для выбора одного из списков. Конструктор устанавливает M так, что каждый список будет содержать около пяти элементов; поэтому для выполнения остальных операций требуется всего несколько проверок.

  private:
    link* heads;
    int N, M;
  public:
    ST(int maxN)
      { N = 0; M = maxN/5;
        heads = new link[M];
        for (int i = 0; i < M; i++) heads[i] = 0;
      }
    Item search(Key v)
      { return searchR(heads[hash(v, M)], v); }
    void insert(Item item)
      { int i = hash(item.key(), M);
        heads[i] = new node(item, heads[i]); N++;
      }
      

Более того, для элементов примитивного типа можно было бы даже исключить M ссылок на эти списки, поместив первые узлы списков в саму таблицу (см. упражнение 14.20). Для неудачных поисков можно считать, что хеш-функция достаточно равномерно перемешивает значения ключей, чтобы поиск в каждом из M списков был равновероятным. Тогда характеристики производительности, рассмотренные в "Таблицы символов и деревья бинарного поиска" , применимы к каждому списку.

Чаще всего для цепочек переполнения используются неупорядоченные списки, поскольку этот подход прост в реализации и эффективен: операция вставить выполняется за постоянное время, а операция найти — за время, пропорциональное N/M. Если ожидается очень большое количество неудачных поисков, их обнаружение можно ускорить в два раза, храня списки в упорядоченном виде, но за счет замедления операции вставить.

Лемма 14.1 тривиальна, поскольку средняя длина списков равна N/M независимо от распределения элементов по спискам. Например, предположим, что все элементы попадают в первый список. Тогда средняя длина списков равна (N + 0 + 0 + ... + 0)/M = N/M. Истинная причина практической пользы хеширования заключается в том, что очень высока вероятность наличия около N/M элементов в каждом списке.

Лемма 14.2. В хеш-таблице с цепочками переполнения, содержащей M списков и N ключей, вероятность того, что количество ключей в каждом списке отличается от N/M на небольшой постоянный коэффициент, очень близка к 1.

Для читателей, которые знакомы с основами вероятностного анализа, приведем краткое изложение этих классических рассуждений. Легко видеть, что вероятность того, что данный список будет содержать к элементов, равна

Здесь выбираются k из N элементов: эти к элементов попадают в данный список с вероятностью 1/M, а остальные N — k элементов не попадают в данный список с вероятностью 1 — 1/M. Обозначив 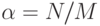, это выражение можно переписать как

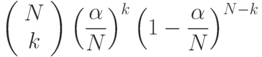
что, согласно классической аппроксимации Пуассона, меньше чем

.

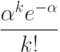
Отсюда следует, что вероятность наличия в списке более чем элементов меньше, чем

.

Для используемых на практике диапазонов параметров эта вероятность исключительно мала. Например, если средняя длина списков равна 20, вероятность того, что в какой-либо список попадут более 40 элементов, меньше чем .

Приведенный анализ — пример классической задачи о размещении: N шаров случайным образом вбрасываются в одну из M урн, и анализируется распределение шаров по урнам. Классический математический анализ этих задач дает и много других интересных фактов, имеющих отношение к изучению алгоритмов хеширования. Например, в соответствии с аппроксимацией Пуассона количество пустых списков близко к 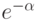. Хотя более интересен факт, что среднее количество элементов, вставленных до первой коллизии, равно приблизительно . Этот результат — решение классической задачи о дне рождения. Например, в соответствии с этими же рассуждениями, при M= 365 среднее количество людей, среди которых найдутся двое с одинаковыми датами рождения, приблизительно равно 24. В соответствии со вторым классическим результатом среднее количество элементов, вставленных прежде, чем в каждом списке окажется по меньшей мере по одному элементу, приблизительно равно MH_M Этот результат — решение классической задачи коллекционера карточек. Например, аналогичный анализ утверждает, что при M = 1280 нужно собрать около 9898 бейсбольных карточек (купонов), прежде чем удастся заполучить по одной карточке для каждого из 40 игроков каждой из 32 команд. Данные результаты весьма показательны для рассмотренных свойств хеширования. Практически они означают, что цепочки переполнения можно успешно использовать, если хеш-функция выдает значения, близкие к случайным (см. раздел ссылок).

Обычно в реализациях цепочек переполнения значение M выбирают достаточно малым, чтобы не тратить понапрасну большие непрерывные участки памяти с пустыми ссылками, но достаточно большим, чтобы последовательный поиск в списках был наиболее эффективным методом. Гибридные методы (вроде использования бинарных деревьев вместо связных списков), вряд ли стоят рассмотрения. Как правило, можно выбирать значение M равным приблизительно одной пятой или одной десятой от ожидаемого количества ключей в таблице, чтобы каждый из списков в среднем содержал порядка 5—10 ключей. Одно из достоинств цепочек переполнения состоит в том, что этот выбор не критичен: при наличии большего, чем ожидалось, количества ключей поиски будут требовать несколько больше времени, чем если бы заранее был выбран больший размер таблицы; при наличии в таблице меньшего количества ключей поиск будет сверхбыстрым при (скорее всего) небольшом дополнительном расходе памяти. Если памяти хватает, значение M можно выбрать достаточно большим, чтобы время поиска было постоянным; если же объем памяти критичен, все-таки можно повысить производительность в M раз, выбрав максимально возможное значение M.

Приведенные в предыдущем абзаце рассуждения относятся к времени поиска. На практике для цепочек переполнения обычно применяются неупорядоченные списки, по двум основным причинам. Во-первых, как уже упоминалось, исключительно быстро выполняется операция вставить: вычисляем хеш-функцию, выделяем память для узла и связываем его с началом соответствующего списка. Во многих приложениях шаг распределения памяти не требуется (поскольку элементами, вставляемыми в таблицу символов, могут быть существующие записи с доступными полями ссылок), и для выполнения операции вставить остается выполнить всего три—четыре машинные инструкции. Второе важное преимущество использования в программе 14.3 реализации с использованием неупорядоченных списков заключается в том, что все списки работают подобно стекам, поэтому можно легко удалить последние вставленные элементы, которые размещаются в начале списков (см. упражнение 14.21). Эта операция важна при реализации таблицы символов с вложенными областями видимости (например, в компиляторе).

Как и в нескольких предыдущих реализациях, клиенту неявно предоставляется выбор способа обработки повторяющихся ключей. Клиент вроде программы 12.11 может перед любой операцией вставить выполнить операцию найти для проверки наличия такого ключа и таким образом обеспечить, что таблица не будет содержать повторяющихся ключей. Другой клиент может сэкономить сопряженные с операцией найти затраты, оставляя дубликаты в таблице и тем самым ускорив выполнение операций вставить.

В общем случае хеширование не подходит для использования в приложениях, в которых требуются реализации операций АТД сортировать и выбрать. Однако хеширование часто используется в типичных ситуациях, когда необходимо использовать таблицу символов с потенциально большим количеством операций найти, вставить и удалить с последующим однократным выводом элементов в порядке их ключей. Одним из примеров такого приложения является таблица символов в компиляторе; другой пример — программа удаления повторяющихся ключей, наподобие программы 12.11. Для обработки этой ситуации в реализации цепочек переполнения в виде неупорядоченных списков нужно воспользоваться одним из методов сортировки, описанных в лекциях 6—10. В реализации с использованием упорядоченных списков сортировку можно выполнить слиянием всех списков (см. упражнение 14.23) за время, пропорциональное Nlg M.

Упражнения

14.16. Сколько времени может потребоваться в худшем случае для вставки N ключей в первоначально пустую таблицу с цепочками переполнения в виде (1) неупорядоченных списков и (2) упорядоченных списков?

14.17. Приведите содержимое хеш-таблицы, образованной вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустую таблицу из M = 5 списков при использовании цепочек переполнения в виде неупорядоченных списков. Для преобразования k-ой буквы алфавита в индекс таблицы используйте хеш-функцию 11k mod M.

14.18. Выполните упражнение 14.17, но для случая упорядоченных списков. Зависит ли ответ от порядка вставки элементов?

14.19. Напишите программу, которая вставляет N случайных целых чисел в таблицу размером N/100 с цепочками переполнения, а затем определяет длину самого короткого и самого длинного списков, при N = 10³, 10⁴, 10⁵ и 10⁶ .

14.20. Измените программу 14.3, чтобы исключить из нее ведущие ссылки с помощью представления таблицы символов в виде массива узлов типа node (каждый элемент таблицы является первым узлом в ее списке).

14.21. Измените программу 14.3, включив в нее для каждого элемента целочисленное поле, значение которого устанавливается равным количеству элементов в таблице на момент вставки элемента. Затем реализуйте функцию, удаляющую все элементы, для которого значение этого поля больше заданного целого числа N.

14.22. Измените реализацию функции search в программе 14.3, чтобы она выводила все элементы с ключами, равными заданному ключу, так же, как это сделано в функции show.

14.23. Разработайте реализацию таблицы символов с цепочками переполнения в виде упорядоченных списков, которая включает деструктор, конструктор копирования и перегруженную операцию присваивания и поддерживает операции создать, подсчитать, найти, вставить, удалить, объединить, выбрать и сортировать для АТД первого класса таблицы символов при поддержке клиентских дескрипторов (см. упражнения 12.6 и 12.7).