|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Сбалансированные деревья
Нисходящие 2-3-4-деревья
Несмотря на гарантию производительности, обеспечиваемую рандомизированными и скошенными BST-деревьями, в обоих случаях не исключается вероятность того, что время выполнения отдельной операции поиска будет линейным. Следовательно, эти методы не помогают ответить на основной вопрос в отношении сбалансированных деревьев: существует ли тип BST-дерева, для которого можно гарантировать логарифмическую зависимость времени выполнения каждой операции вставить и найти от размеров дерева? В этом и следующем разделах мы рассмотрим абстрактное обобщение BST-деревьев и их абстрактное представление в виде типа BST-дерева, которые позволяют утвердительно ответить на этот вопрос.
Для гарантии сбалансированности создаваемых BST-деревьев используемые структуры деревьев должны обладать определенной гибкостью. Для получения такой гибкости предположим, что узлы в наших деревьях могут содержать более одного ключа. А именно, мы допустим существование 3-узлов и 4-узлов, которые могут содержать, соответственно, два и три ключа. 3-узлы содержат три ссылки: одна на все элементы, ключи которых меньше обоих его ключей, одна на все элементы, ключи которых имеют значения между двумя его ключами, и одна на все элементы, ключи которых больше обоих его ключей. Аналогично, 4-узел имеет четыре ссылки: по одной для каждого из интервалов, определенных его тремя ключами. Тогда узлы в стандартном BST-дереве можно было бы называть 2-узлами: они содержат один ключ и две ссылки. Позже мы рассмотрим эффективные способы определения и реализации базовых операций с этими расширенными узлами; пока же будем считать, что есть удобные способы работы с ними, и посмотрим, как они позволяют формировать деревья.
Определение 13.1. 2-3-4-дерево поиска — это либо пустое дерево, либо дерево, содержащее три типа узлов: 2-узлы — с одним ключом, левой ссылкой на дерево с меньшими ключами и правой ссылкой на дерево с большими ключами; 3-узлы — с двумя ключами, с левой ссылкой на дерево с меньшими ключами, средней ссылкой на дерево, ключи которых имеют значения между значениями ключей данного узла, и правой ссылкой на дерево с большими ключами; и 4-узлы с тремя ключами и четырьмя ссылками на деревья, значения ключей которых определены диапазонами, образованными ключами узла.
Определение 13.2. Сбалансированное 2-3-4-дерево поиска — это 2-3-4-дерево поиска, все ссылки на пустые деревья которого расположены на одинаковом расстоянии от корня.
В этой главе термин 2-3-4-дерево будет применяться к сбалансированным 2-3-4-деревьям поиска (в других контекстах он означает более общую структуру). Пример 2-3-4-дерева приведен на рис. 13.10.
Алгоритм поиска ключей в таком дереве представляет собой обобщение алгоритма поиска для BST-деревьев. Чтобы выяснить, находится ли ключ в дереве, мы сравниваем его с ключами в корне: если он равен любому из них, поиск успешен; в противном случае мы переходим по ссылке от корня к поддереву, соответствующему множеству значений ключей, к которому принадлежит искомый ключ, и затем рекурсивно выполняем поиск в этом дереве. Существует ряд способов представления 2-, 3- и 4-узлов и организации поиска соответствующей ссылки; мы отложим рассмотрение этих решений до раздела 13.4, где будет рассмотрено очень удобное решение.
Для вставки нового узла в 2-3-4-дерево можно было бы, как в BST-деревьях, выполнить неудачный поиск, а затем присоединить узел, но при этом новое дерево оказалось бы несбалансированным. Основная причина важности 2-3-4-деревьев состоит в том, что они позволяют выполнять вставки, всегда сохраняя полную сбалансированность дерева. Например, легко видеть, что делать, если поиск заканчивается на 2-узле: достаточно преобразовать его в 3-узел. Аналогично, если поиск заканчивается на 3-узле, его достаточно преобразовать в 4-узел. Но что делать, если поиск прерывается на 4-узле? Решение состоит в том, что можно найти место для нового ключа, сохраняя сбалансированность дерева, вначале разделив 4-узел на два 2-узла, и затем передав средний узел вверх к родительскому узлу. Эти три описанных случая показаны на рис. 13.11.
А что делать, если необходимо разбить 4-узел, родительский узел которого также является 4-узлом? Одним из возможных выходов было бы разбиение и родительского узла, но узел-предок также может оказаться 4-узлом и т.д. — возможно, пришлось бы разделять узлы на всем пути вверх по дереву. Более простой подход — обеспечить, чтобы путь поиска не завершался в 4-узле, разбивая любой 4-узел, попадающийся при следовании вниз по дереву.
А именно, каждый раз, когда встречается 2-узел с дочерним 4-узлом, такая пара преобразуется в 3-узел с двумя дочерними 2-узлами; а когда встречается 3-узел с дочерним 4-узлом, такая пара преобразуется в 4-узел с двумя дочерними 2-узлами (см. рис. 13.12). Разбиение 4-узлов возможно потому, что можно перемещать не только ключи, но и ссылки. Два 2-узла имеют столько же (четыре) ссылок, что и 4-узел, поэтому разбиение можно выполнить, не внося никаких изменений ниже (или выше) разбиваемого узла. 3-узел не преобразуется в 4-узел одним лишь добавлением еще одного ключа; требуется еще одна ссылка (в данном случае — дополнительная ссылка, созданная разбиением). Очень важно, что эти преобразования являются чисто локальными: не нужно проверять или изменять никакую часть дерева, кроме показанной на рис. 13.12. Каждое преобразование передает один из ключей 4-узла в его родительский узел и соответствующим образом преобразует ссылки.
Спускаясь вниз по дереву, не нужно явно беспокоиться о том, что родительский узел текущего узла является 4-узлом: ведь выполняемые преобразования обеспечивают, что при прохождении каждого узла в дереве мы попадаем в узел, который не является потомком 4-узла. В частности, при достижении нижней части дерева мы оказываемся не в 4-узле и можем вставить новый узел, непосредственно преобразовав 2-узел в 3-узел, либо 3-узел в 4-узел. Вставку можно считать разбиением воображаемого 4-узла в нижней части дерева, передающим вверх новый ключ.
Еще один нюанс: когда корень дерева становится 4-узлом, мы просто разбиваем его, преобразуя в треугольник, состоящий из трех 2-узлов, как для первого разбиваемого узла в предыдущем примере. Разбиение корня после вставки несколько удобнее ожидания очередной вставки для выполнения разбиения, поскольку в этом случае не нужно заботиться о родительском узле корня. Разбиение корня (и только эта операция) приводит к увеличению высоты дерева на один уровень.
На этом рисунке изображено 2-3-4-дерево, содержащее ключи A S R C H I N G E X M P L.
В таком дереве ключ можно отыскать, используя ключи в корневом узле для нахождения ссылки на нужное поддерево, с последующим рекурсивным продолжением поиска. Например, для поиска ключа P в этом дереве нужно пройти по правой ссылке от корня, поскольку P больше I, затем — по средней ссылке от правого дочернего узла корня, поскольку P находится между N и R, и, наконец, завершить успешный поиск в 2-узле, содержащем ключ P.
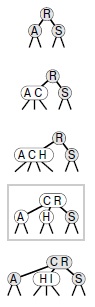
2-3-4-дерево, состоящее только из 2-узлов, аналогично BST-дереву (вверху). Ключ C можно вставить, преобразовав 2-узел, в котором прерывается поиск C, в 3-узел (второй сверху рисунок). Аналогично можно вставить ключ H, преобразовав 3-узел, в котором прерывается его поиск, в 4-узел (третий сверху рисунок). Но вставка ключа I выполняется сложнее, поскольку его поиск прерывается в 4-узле. Мы разбиваем 4-узел, передаем его средний ключ родительскому узлу, и преобразуем этот узел в 3-узел (четвертый сверху рисунок в рамке). Такое преобразование создает допустимое 2-3-4-дерево, в нижней части которого появляется место для I . И, наконец, мы вставляем I в 2-узел, на котором теперь прерывается поиск, и преобразуем этот узел в 3-узел (нижний рисунок).
В 2-3-4-дереве любой 4-узел, который не является дочерним узлом 4-узла, можно разбить на два 2-узла, передав его среднюю запись родительскому узлу. 2-узел с дочерним 4-узлом (вверху слева) становится 3-узлом с двумя дочерними 2-узлами (вверху справа), а 3-узел с дочерним 4-узлом (внизу слева) становится 4-узлом с двумя дочерними 2-узлами (внизу справа).
Построение 2-3-4-дерева
Здесь показан результат вставки элементов с ключами A S E R C H I N G X в первоначально пустое 2-3-4-дерево. Каждый встречающийся по пути поиска 4-узел разбивается, обеспечивая свободное место для нового элемента в нижней части дерева.
На рис. 13.13 показано построение 2-3-4-дерева последовательной вставкой набора ключей. В отличие от стандартных BST-деревьев, которые разрастаются вниз от вершины, эти деревья растут снизу вверх. Поскольку 4-узлы разбиваются на пути от вершины вниз, такие деревья называются нисходящими 2-3-4-деревьями. Этот алгоритм важен, поскольку он создает практически идеально сбалансированные деревья поиска, хотя в процессе прохождения по дереву выполняется всего лишь несколько локальных преобразований.
Лемма 13.6. При поиске в 2-3-4-деревьях из N узлов посещается максимум lgN+1 узлов.
Каждый внешний узел находится на одинаковом расстоянии от корня: выполняемые преобразования не оказывают никакого влияния на расстояние между любым узлом и корнем, за исключением случая, когда выполняется разбиение корня (в этом случае расстояние между всеми узлами и корнем увеличивается на 1). Если все узлы являются 2-узлами, приведенное утверждение справедливо, поскольку такое дерево подобно полному бинарному дереву; если в дереве присутствуют 3- и 4-узлы, высота может быть только меньше. 
Лемма 13.7. Для вставок в 2-3-4-деревьях из N узлов требуется разбиение менее lg N + 1 узлов в худшем случае и, скорее всего, менее одного разбиения узла в среднем.
В самом худшем случае все узлы на пути к точке вставки являются 4-узлами, и все потребуется разбить. Но в дереве, построенном из случайной перестановки N элементов, маловероятен не только этот худший случай, но и в среднем, вероятно, потребуется очень мало операций разбиения, поскольку 4-узлы в деревьях встречаются не так часто. Например, в большом дереве на рис. 13.14
рис.
13.14 все 4-узлы, кроме двух, расположены на нижнем уровне. До сих пор специалистам не удавалось аналитически точно проанализировать производительность 2-3-4-деревьев, но из эмпирически полученных результатов видно, что для балансировки деревьев используется очень мало разбиений. Худший случай равен лишь lg N, а в практических ситуациях и он недостижим. 
Приведенного описания достаточно для определения алгоритма поиска с использованием 2-3-4-деревьев, который гарантирует достаточно высокую производительность в худшем случае. Однако мы находимся лишь на полпути к реализации. Можно написать алгоритмы, действительно выполняющие преобразования с различными типами данных, представляющими 2-, 3- и 4-узлы, но в большинстве встречающихся задач реализация такого непосредственного представления не очень удобна. Как и в случае скошенных BST-деревьев, дополнительные расходы на обработку более сложных узлов могут сделать алгоритмы более медленными, чем стандартный поиск по BST-дереву. Главное назначение балансировки — страховка от худшего случая, но хотелось бы, чтобы затраты, связанные с этим, были низкими, и чтобы не было дополнительных затрат при каждом выполнении алгоритма. К счастью, как будет показано в разделе 13.4, существует довольно простое представление 2-, 3- и 4-узлов, которое позволяет выполнять преобразования однотипным способом при небольших дополнительных затратах по сравнению со стандартным поиском в бинарном дереве.
Это 2-3-4-дерево — результат 200 случайных вставок в первоначально пустое дерево. Все пути поиска в дереве содержат не более шести узлов.
Описанный алгоритм — всего лишь один из возможных способов поддержания баланса в 2-3-4-деревьях поиска. Разработаны и некоторые другие методы, позволяющие достичь таких же результатов.
Например, можно выполнять балансировку снизу вверх. Вначале в дереве выполняется поиск расположенного в нижней части дерева узла, которому должен принадлежать вставляемый элемент. Если этот узел является 2-узлом или 3-узлом, он преобразуется в 3-узел или 4-узел, как описывалось ранее. Если это 4-узел, он разбивается, как и ранее (со вставкой нового элемента в один из результирующих 2-узлов в нижней части), и средний элемент вставляется в родительский узел, если тот является 2- или 3-узлом. Если родительский узел является 4-узлом, он также разбивается (со вставкой среднего узла с нижнего уровня в соответствующий 2-узел), а средний элемент вставляется в его родительский узел, если тот является 2- или 3-узлом. Если узел-дед также является 4-узлом, мы продолжаем этот подъем по дереву, разбивая 4-узлы до тех пор, пока на пути поиска не встретится 2-узел или 3-узел.
Такой вид восходящей балансировки можно выполнять в деревьях, которые содержат только 2- или 3-узлы (и не имеют 4-узлов). Это подход ведет к большему количеству операций разбиения узлов во время выполнения алгоритма, но его проще программировать, поскольку приходится учитывать меньше случаев. Еще один подход уменьшает количество разбиений узлов, отыскивая перед разбиением 4-узла его родственные узлы, не являющиеся 4-узлами.
Как будет показано в разделе 13.4, реализации всех этих методов основаны на одной и той же рекурсивной схеме. В "Внешний поиск" также будут рассмотрены обобщения этих методов. Основное преимущество рассматриваемого нисходящего подхода по сравнению с другими методами заключается в том, что необходимая сбалансированность может быть достигнута в результате одного нисходящего прохода по дереву.
Упражнения
13.39. Нарисуйте сбалансированное 2-3-4-дерево поиска, образованное нисходящими вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево.
13.40. Нарисуйте сбалансированное 2-3-4-дерево поиска, образованное восходящими вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево.
13.41. Какова минимальная и максимальная возможная высота сбалансированных 2-3-4-деревьев, содержащих N узлов?
13.42. Какова минимальная и максимальная возможная высота сбалансированных 2-3-4-деревьев бинарного поиска, содержащих N узлов?
13.43. Нарисуйте все структурно различные сбалансированные 2-3-4-деревья бинарного поиска, содержащие N ключей, для  .
.
13.44. Найдите вероятность того, что каждое из деревьев, нарисованных в упражнении 13.43, является результатом вставки N случайных различных элементов в первоначально пустое дерево.
13.45. Составьте таблицу, содержащую количество изоморфных деревьев из упражнения 13.43 для каждого значения N — в том смысле, что они могут быть преобразованы одно в другое путем обмена поддеревьев в узлах.
13.46. Опишите алгоритмы поиска и вставки в сбалансированные 2-3-4-5-6-деревья поиска.
13.47. Нарисуйте несбалансированное 2-3-4-дерево поиска, образованное вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево с использованием следующего метода. Если поиск завершается в 2-или 3-узле, он преобразовывается в 3- или 4-узел, как в сбалансированном алгоритме; если поиск завершается в 4-узле, соответствующая ссылка в этом 4-узле заменяется новым 2-узлом.