Очереди с приоритетами и пирамидальная сортировка

Биномиальные очереди

Ни одна из рассмотренных выше реализаций не может обеспечить эффективное выполнение в худшем случае сразу всех операций объединить, извлечь наибольший и вставить. Неупорядоченные связные списки быстро выполняют операции объединить и вставить, но медленно — извлечь наибольший; упорядоченные связные списки быстро выполняют операцию извлечь наибольший, но медленно — объединить и вставить; в пирамидальном дереве быстро выполняются вставить и извлечь наибольший, но медленно — операция объединить и т.д. (см. таблицу 9.1). Для приложений, в которых характерны частые или объемные операции объединить, нужны более совершенные структуры данных.

Здесь под термином " эффективная " понимается, что операции должны выполняться в худшем случае за не более чем логарифмическое время. Это ограничение сразу исключает представление в виде массива, поскольку очевидно, что два массива можно объединить только путем пересылки всех элементов по крайней мере одного из массивов. Представление в виде неупорядоченного двухсвязного списка из программы 9.9 выполняет операцию объединить за постоянное время, но требует просмотра всего списка при выполнении операции извлечь наибольший. Использование двухсвязных упорядоченных списков (см. упражнение 9.39) позволяет выполнять за постоянное время операцию извлечь наибольший, однако требует линейного времени для выполнения слияния списков операцией объединить.

Разработаны многочисленные структуры данных, способные поддерживать эффективные реализации всех операций над очередями с приоритетами. Большая их часть основана на прямом связном представлении пирамидально упорядоченных деревьев. Две связи необходимы для продвижения вниз по дереву (либо к двум дочерним узлам в бинарном дереве, либо к первому дочернему узлу и к следующему родственному узлу в бинарном представлении дерева общего вида), и одна связь с родителем нужна для продвижения вверх по дереву. Разработка реализаций операций, устанавливающих пирамидальный порядок на любой (пирамидально упорядоченной) древовидной форме с явно определенными узлами и связями или на других представлениях в общем случае не требует особых ухищрений. Основная трудность сопряжена с такими динамическими операциями как вставить, извлечь и объединить, которые требуют модификации древовидных структур. В основу различных структур данных положены различные стратегии модификации древовидных структур, обеспечивающие баланс в дереве. Эти алгоритмы используют деревья, обладающие большей гибкостью, нежели полные деревья, и поддерживают их достаточно сбалансированными, чтобы время выполнения было не более чем логарифмическим.

Затраты ресурсов на использование трехсвязных структур могут оказаться обременительными: необходимо гарантировать, что конкретная реализация правильно использует три указателя во всех случаях (см. упражнение 9.40). Более того, во многих практических ситуациях трудно обосновать необходимость эффективной реализации всех операций, так что, перед тем как браться за подобную реализацию, следует хорошо обдумать этот вопрос. Но ведь не менее трудно доказать, что эффективные реализации не нужны, и усилия, потраченные на то, чтобы все операции над очередями с приоритетами были быстрыми, могут окупиться. Как бы то ни было, переход от пирамидальных деревьев к структурам данных, позволяющим эффективно реализовать операции объединить, вставить и извлечь наибольший, интересен сам по себе и достоин подробного изучения.

Даже для связных представлений деревьев требование его пирамидальной упорядоченности и требование полноты пирамидально упорядоченного бинарного дерева являются чрезмерно жесткими для получения эффективной реализации операции объединить. Если имеются два пирамидально упорядоченных дерева, то как слить их в одно? Например, если одно из этих деревьев содержит 1023 узла, а другое — 255 узлов, то как слить их, чтобы получить дерево из 1278 узлов и не затронуть более 10—20 узлов? Похоже, что задача слияния пирамидально упорядоченных деревьев вообще неразрешима, если эти деревья должны быть пирамидально упорядоченными и полными. Поэтому были предложены различные более совершенные структуры данных, способные ослабить требования пирамидальной упорядоченности и сбалансированности и придать структурам данных большую гибкость, необходимую для эффективной реализации операции объединить. Сейчас мы рассмотрим оригинальное решение этой проблемы, получившее название биномиальной очереди (binomial queue) и предложенное Вильемином (Vuillemin) в 1978 г.

Вначале следует отметить, что операция объединить тривиальна для одного специального типа дерева с ослабленным требованием пирамидальной упорядоченности.

Биномиальные деревья и пирамидальные деревья степени 2 — это одно и то же. Мы будем работать с обоими представлениями, поскольку биномиальные деревья легче отобразить визуально, а простое представление деревьев степени 2 приводит к более простой реализации. Особенно важны следующие факторы, непосредственно следующие из определений:

• Количество узлов дерева степени 2 есть степень числа 2.
• Ключ любого узла не больше ключа корня.
• Биномиальные деревья пирамидально упорядочены.

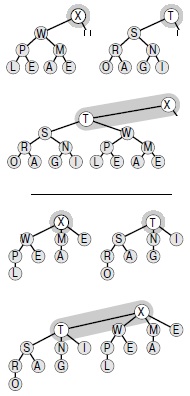
Биномиальные алгоритмы обработки биномиальных очередей основаны на тривиальной операции объединения двух пирамидальных деревьев степени 2 с одинаковым количеством узлов. В результате объединения получается пирамидальное дерево с вдвое большим количеством узлов, которое совсем нетрудно построить (см. рис. 9.15). Корневой узел с большим ключом становится корнем результирующего дерева, корень другого дерева при этом становится левым потомком корня результирующего дерева, а его левое поддерево становится правым поддеревом другого корневого узла. При связном представлении деревьев операция объединения выполняется за постоянное время: для этого нужно лишь настроить две ссылки вверху дерева. Реализация этой операции приведена в программе 9.13. Эта базовая операция является основой общего решения задачи реализации очереди с приоритетами без медленных операций, которое было предложено Вильемином.

Программа 9.13. Объединение двух пирамидальных деревьев степени 2 одинакового размера

Чтобы объединить два пирамидальных дерева степени 2 одинакового размера в одно пирамидальное дерево степени 2 двойного размера, достаточно изменить лишь несколько ссылок. Эта функция, которая в реализации определена как приватная функция-член, является одним из ключевых факторов, обеспечивающих эффективность алгоритма биномиальной очереди.

  static link pair(link p, link q)
    { if (p->item < q->item)
        { p->r = q->l; q->l = p; return q; }
      else
        { q->r = p->l; p->l = q; return p; }
    }
        

Биномиальная очередь из N элементов содержит по одному пирамидальному дереву на каждый бит двоичного представления числа N. Например, биномиальная очередь из 13 узлов содержит одно пирамидальное дерево с 8 узлами, одно с 4 узлами и одно с 1 узлом, как показано на рис. 9.16. Биномиальная очередь размера N содержит максимум lg N пирамидальных деревьев степени 2, и высота каждого не больше lg N.

В соответствии с определениями 9.5 и 9.6, пирамидальные деревья степени 2 (и дескрипторы их элементов) представляются в виде ссылок на узлы, содержащие ключ и две ссылки (как в явном представлении турниров деревом на рис. 5.10), а биномиальные очереди представляются как массивы пирамидальных деревьев степени 2 путем включения в реализацию программы 9.8 следующих приватных членов:

  struct node
    { Item item; node *l, *r;
      node(Item v)
        { item = v; l = 0; r = 0; }
    };
    typedef node *link;
    link* bq;
        

Размеры массивов невелики, и высота деревьев тоже, а само это представление обладает достаточной гибкостью для реализации всех операций над очередями с приоритетами за менее чем lg N шагов, в чем мы сейчас убедимся.

Рис. 9.15. Объединение двух пирамидальных деревьев степени 2 одинакового размера

Для объединения двух пирамидальных деревьев степени 2 (вверху), мы помещаем больший из двух корней в корень результирующего дерева, при этом поддерево (левое) этого корня становится правым поддеревом другого исходного корня. Если операнды содержат 2ⁿ узлов, то результат содержит 2ⁿ+1 узлов. Если операндами являются левосторонне пирамидально упорядоченные деревья, то такой же порядок сохраняется и в результирующем дереве, при этом ключ с наибольшим значением находится в корне. Представление этой же операции в виде пирамидально упорядоченного биномиального дерева показано под чертой.

Рис. 9.16. Биномиальная очередь размера 13

Биномиальная очередь размера N — это список левосторонне пирамидально упорядоченных деревьев степени 2, по одному на каждый бит двоичного представления числа N. Таким образом, биномиальная очередь размера 13 = 1101₂ состоит из одного 8-узлового пирамидального дерева, одного 4-узлового и одного 1-узлового деревьев. На рисунке показано представление одной и той же биномиальной очереди в виде левосторонне пирамидально упорядоченного дерева степени 2 (сверху) и в виде биномиального пирамидально упорядоченного дерева (внизу).

Сначала рассмотрим операцию вставить. Процесс вставки нового элемента в биномиальную очередь в точности отображает процесс увеличения двоичного числа на единицу. Чтобы увеличить двоичное число на единицу, мы двигаемся справа налево, выполняя перенос заменой 1 на 0, т.к. 1 + 1 = 10₂, пока не обнаружим самый правый 0, который заменяем единицей. Аналогичным образом, чтобы добавить в биномиальную очередь новый элемент, мы продвигаемся справа налево, сливая деревья, соответствующие битам 1, с деревом переноса, пока не дойдем до самой правой пустой позиции, в которую и помещаем дерево переноса.

В частности, для вставки нового элемента в биномиальную очередь мы превращаем этот элемент в пирамидальное 1-дерево. Далее, если N четно (самый правый разряд равен 0), мы просто помещаем это 1-дерево в самую правую пустую позицию биномиальной очереди. Если N нечетно (самый правый разряд равен 1), мы объединяем 1-дерево, соответствующее новому элементу, с 1-деревом в самой крайней правой позиции биномиальной очереди и получаем 2-дерево переноса. Если позиция, соответствующая 2 в биномиальной очереди, пуста, то дерево переноса помещается в эту позицию, иначе 2-дерево переноса сливается с 2-деревом из биномиальной очереди, образуя при этом 4-дерево переноса — и так до тех пор, пока в биномиальной очереди не встретится пустая позиция. Этот процесс показан на рис. 9.17, а его реализация приведена в программе 9.14.

Рис. 9.17. Вставка нового элемента в биномиальную очередь

Добавление элемента в биномиальную очередь из семи узлов аналогично выполнению арифметической операции двоичного сложения 111₂ + 1 = 1000₂ с переносом в каждом разряде. В результате получается биномиальная очередь, показанная внизу, которая состоит из 8-дерева, а 4-, 2- и 1-деревья отсутствуют.