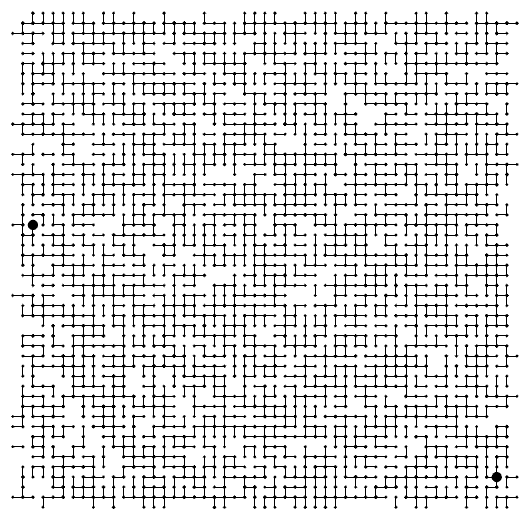Введение

Пример задачи: связность

Предположим, что имеется последовательность пар целых чисел, в которой каждое целое число представляет объект некоторого типа, а пара p-q означает "p связано с q". Предполагается, что отношение "связано с" является транзитивным: если p связано с q, а q связано с r, то p связано с r. Задача состоит в написании программы для исключения лишних пар из набора: когда программа вводит пару p-q, она должна выводить эту пару только в том случае, если из просмотренных до данного момента пар не следует, что p связано с q. Если в соответствии с ранее просмотренными парами следует, что p связано с q, программа должна игнорировать пару p-q и переходить ко вводу следующей пары. Пример такого процесса показан на рис. 1.1.

Рис. 1.1. Пример связности

При заданной последовательности пар целых чисел, представляющих связи между объектами (слева) алгоритм определения связности должен выводить только те пары, которые определяют новые связи (в центре). Например, пара 2-9 не должна выводиться, поскольку связь 2-3-4-9 определяется ранее указанными связями (подтверждение этого показано справа).

Задача состоит в разработке программы, которая может запомнить достаточный объем информации о просмотренных парах, чтобы решить, связана ли новая пара объектов. Неформально задачу разработки такого метода мы назовем задачей связности. Эта задача возникает в ряде важных приложений. Для подтверждения всеобщего характера этой задачи мы кратко рассмотрим три примера.

Например, целые числа могли бы представлять компьютеры в большой сети, а пары могли бы представлять соединения в сети. Тогда такая программа могла бы использоваться для определения того, нужно ли устанавливать новое прямое соединение между p и q, чтобы они могли обмениваться информацией, или же для установки коммуникационного пути можно использовать существующие соединения. В подобных приложениях может потребоваться обработка миллионов точек и миллиардов или более соединений. Как мы увидим, решить задачу для такого приложения было бы невозможно без эффективного алгоритма. Аналогично, целые числа могли бы представлять контакты в электрической сети, а пары могли бы представлять связывающие их проводники. В этом случае программу можно было бы использовать для определения способа соединения всех точек без каких-либо избыточных соединений, если это возможно. Не существует никакой гарантии, что связей в списке окажется достаточно для соединения всех точек — действительно, вскоре мы увидим, что определение факта, так ли это, может быть основным применением нашей программы.

На рис. 1.2 показаны эти два типа применений на более сложном примере. Изучение этого рисунка дает представление о сложности задачи связности: как можно быстро выяснить, являются ли любые две заданные точки в такой сети связанными?

Еще один пример встречается в некоторых средах программирования, в которых два имени переменных можно объявлять эквивалентными. Задача заключается в возможности определения, являются ли два заданных имени эквивалентными, после считывания последовательности таких объявлений. Это применение — одно из первых, обусловивших разработку нескольких алгоритмов, которые мы рассмотрим ниже. Как будет показано далее, оно устанавливает непосредственную связь между рассматриваемой задачей и простой абстракцией, предоставляющей способ сделать алгоритмы полезными для широкого множества приложений.

Такие приложения, как задача установления эквивалентности имен переменных, описанная в предыдущем абзаце, требует, чтобы с каждым отдельным именем переменной было сопоставлено целое число. Это сопоставление подразумевается также и в описанных приложениях сетевого соединения и соединения в электрической цепи. В лекциях 10—16 мы рассмотрим ряд алгоритмов, которые могут эффективно обеспечить такое сопоставление. Таким образом, в этой лекции без ущерба для общности можно предположить, что имеется N объектов с целочисленными именами от 0 до N — 1 .

Рис. 1.2. Большой пример задачи связности

Объекты, задействованные в задаче связности, могут представлять собой точки соединений, а пары могут быть соединениями между ними — как показано в этом идеализированном примере, который мог бы представлять провода, соединяющие здания в городе или компоненты в компьютерной микросхеме. Это графическое представление позволяет человеку выявить несвязанные узлы, но алгоритм должен работать только с переданными ему парами целых чисел. Связаны ли два узла, помеченные большими черными точками?

Нам требуется программа, которая выполняет конкретную, вполне определенную задачу. Существует множество других связанных с этой задач, решение которых также может потребоваться. Один из первых вопросов, который необходимо решить при разработке алгоритма — это убедиться, что задача определена приемлемым образом. Чем выше требования к алгоритму, тем больше времени и объема памяти может потребоваться для выполнения задачи. Это соотношение невозможно в точности определить заранее, и часто определение задачи приходится изменять, когда выясняется, что ее трудно решить, либо решение требует слишком больших затрат, или же когда, при удачном стечении обстоятельств, выясняется, что алгоритм может предоставить более полезную информацию, чем требовалось от него в исходном определении.

Например, приведенное определение задачи связности требует только, чтобы программа как-либо узнавала, является ли данная пара p-q связанной, но не обязательно демонстрировала любой или все способы соединения этой пары. Добавление в определение такого требования усложнило бы задачу и привело к другому семейству алгоритмов, которое будет кратко рассматриваться в "Рекурсия и деревья" и подробно — в части VII.

Упомянутые в предыдущем абзаце определения требуют больше информации, чем первоначальное; может также требоваться и меньше информации. Например, может потребоваться просто ответить на вопрос: "Достаточно ли M связей для соединения всех N объектов?". Эта задача показывает, что для разработки эффективных алгоритмов часто требуется выполнение умозаключений об абстрактных обрабатываемых объектах на высоком уровне. В данном случае из фундаментальных положений теории графов следует, что все N объектов связаны тогда и только тогда, когда количество пар, образованных алгоритмом решения задачи связности, равно точно N — 1 (см. "Рекурсия и деревья" ). Иначе говоря, алгоритм решения задачи связности никогда не выводит более N — 1 пар, поскольку как только он выведет N — 1 пару, любая встретившаяся после этого пара будет уже связанной. Соответственно, можно создать программу, отвечающую "да-нет" на только что поставленный вопрос, изменив программу, которая решает задачу связности, на такую, которая увеличивает значение счетчика, а не записывает ранее не связанную пару, отвечая "да", когда значение счетчика достигает N— 1 , и "нет", если это не происходит. Этот вопрос — всего лишь один из множества вопросов, которые могут возникнуть относительно связности. Входной набор пар называется графом (graph), а выходной набор пар — остовным деревом (spanning tree) этого графа, которое связывает все объекты. Свойства графов, остовных деревьев и всевозможные связанные с ними алгоритмы будут рассматриваться в части VII.

Имеет смысл попытаться определить основные операции, которые будут выполняться для решения задачи связности, чтобы любой алгоритм, разрабатываемый для ее решения, был полезен и для ряда аналогичных задач. В частности, при получении каждой новой пары вначале необходимо определить, представляет ли она новое соединение, а затем внедрить информацию об обнаруженном соединении в общую картину о связности объектов для проверки соединений, которые будут наблюдаться в будущем. Мы инкапсулируем эти две задачи в виде абстрактных операций, считая целочисленные вводимые значения представляющими элементы в абстрактных наборах, а затем разработаем алгоритмы и структуры данных, которые могут:

• находить набор, содержащий данный элемент
• замещать наборы, содержащие два данных элемента, их объединением.

Организация алгоритмов посредством этих абстрактных операций, похоже, не отсекает никакие варианты решения задачи связности, и эти операции могут оказаться полезными при решении других задач. Разработка уровней абстракции с еще большими возможностями — важный процесс в компьютерных науках в целом и в разработке алгоритмов в частности, и в этом курсе мы будем обращаться к нему многократно. В данной лекции для разработки программ решения задачи связности мы используем неформальное абстрактное представление; а в "Абстрактные типы данных" эти абстракции будут выражены в коде C++.

Задача связности легко решается с помощью абстрактных операций поиск (find) и объединение (union). После считывания новой пары p-q мы выполняем операцию поиск для каждого члена пары. Если оба члена пары находятся в одном множестве, мы переходим к следующей паре; если нет, то выполняем операцию объединение и записываем пару. Наборы представляют собой связанные компоненты: подмножества объектов, характеризующиеся тем, что любые два объекта в данном компоненте связаны. Этот подход сводит разработку алгоритмического решения задачи связности к задачам определения структуры данных, которая представляет множества, и разработке алгоритмов объединение и поиск, которые эффективно используют эту структуру данных.

Существует много возможных способов представления и обработки абстрактных множеств. В этой лекции основное внимание уделяется поиску представления, которое может эффективно поддерживать операции объединение и поиск, необходимые для решения задачи связности.

Упражнения

1.1. Приведите выходные данные, которые должен выдавать алгоритм связности для входных пар 0-2, 1-4, 2-5, 3-6, 0-4, 6-0 и 1-3.

1.2. Перечислите все различные способы связывания двух различных объектов, показанных в примере на рис. 1.1.

1.3. Опишите простой метод подсчета количества наборов, остающихся после применения операций объединение и поиск для решения задачи связности, как описано в тексте.