Теории и модели
Полные теории
В этом разделе мы попытаемся систематизировать уже известные нам понятия и факты.
- Начнем с напоминаний. Сигнатурой мы называли набор предикатных и функциональных символов. Среди формул данной сигнатуры выделяют замкнутые (формулы без параметров). Сигнатура имеет интерпретации, в которых замкнутые формулы этой сигнатуры бывают истинными и ложными. Произвольное множество замкнутых формул данной сигнатуры называется теорией в этой сигнатуре. Моделью теории называется интерпретация, в которой все формулы теории истинны. Теория называется совместной, если она имеет модель.
- Теория называется теорией с равенством, если она включает в себя аксиомы равенства (а ее сигнатура содержит символ равенства). Интерпретация теории с равенством называется нормальной, если равенство интерпретируется как совпадение элементов носителя интерпретации. Совместная теория с равенством имеет нормальную модель (получаемую из произвольной модели факторизацией по отношению равенства).
-
Говорят, что замкнутая формула
 выводима в теории
выводима в теории  (является теоремой теории
(является теоремой теории  ),
если формула
),
если формула  получается из аксиом исчисления предикатов
и формул теории
получается из аксиом исчисления предикатов
и формул теории  по правилам вывода. (Обозначение:
по правилам вывода. (Обозначение: 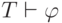 .)
.)Формула
 выводима в теории
выводима в теории  тогда и
только тогда, когда в исчислении предикатов выводится некоторая формула вида
тогда и
только тогда, когда в исчислении предикатов выводится некоторая формула вида  , где
, где 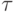 — конъюнкция конечного
числа формул из
— конъюнкция конечного
числа формул из  .
.Формула
 семантически следует из
семантически следует из  , если она истинна в любой
модели теории
, если она истинна в любой
модели теории  (обозначение:
(обозначение:  ).
Семантическое следование равносильно выводимости
(теорема 51). Взяв в качестве
).
Семантическое следование равносильно выводимости
(теорема 51). Взяв в качестве  тождественно ложную формулу
тождественно ложную формулу 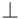 (скажем, отрицание
тавтологии), приходим к понятиям противоречивости
(
(скажем, отрицание
тавтологии), приходим к понятиям противоречивости
(  ) и несовместности
(
) и несовместности
(  ,
,  не имеет моделей).
В противоречивой теории выводима любая формула (соответствующей сигнатуры).
не имеет моделей).
В противоречивой теории выводима любая формула (соответствующей сигнатуры). - Непротиворечивая теория
 полна (в данной сигнатуре), если для
любой замкнутой формулы
полна (в данной сигнатуре), если для
любой замкнутой формулы  этой сигнатуры либо формула
этой сигнатуры либо формула  , либо ее отрицание
, либо ее отрицание  выводится
из
выводится
из  .
. - Для произвольной интерпретации
 произвольной
сигнатуры
произвольной
сигнатуры  можно рассмотреть элементарную теорию
интерпретации
можно рассмотреть элементарную теорию
интерпретации  , обозначаемую
, обозначаемую  и состоящую из всех
истинных в
и состоящую из всех
истинных в  замкнутых формул сигнатуры
замкнутых формул сигнатуры  .
Очевидно, эта теория полна (одна из формул
.
Очевидно, эта теория полна (одна из формул  и
и  ей принадлежит). Две интерпретации
ей принадлежит). Две интерпретации  и
и  элементарно эквивалентны, если
элементарно эквивалентны, если  .
. - Теория
 называется конечно аксиоматизируемой,
если существует конечное множество
называется конечно аксиоматизируемой,
если существует конечное множество  теорем теории
теорем теории  , из которых
выводятся все утверждения из
, из которых
выводятся все утверждения из  (другими словами, если существует
конечная теория, имеющая то же самое множество теорем).
(другими словами, если существует
конечная теория, имеющая то же самое множество теорем). - Теория с равенством, имеющая конечную или счетную сигнатуру, называется категоричной в счетной мощности, если все ее счетные нормальные модели изоморфны. Категоричность в данной несчетной мощности определяется аналогично.
- Теория с конечной сигнатурой называется разрешимой, если существует алгоритм, который по произвольной замкнутой формуле определяет, выводима ли она в этой теории или нет.
117. Покажите, что добавление к теории любой ее теоремы не меняет множества теорем.
Прежде чем переходить к примерам, сделаем два простых наблюдения.
Теорема 65 (критерий Лося-Воота). Непротиворечивая теория  с равенством
в конечной или счетной сигнатуре, не имеющая конечных моделей и
категоричная в счетной мощности, полна.
с равенством
в конечной или счетной сигнатуре, не имеющая конечных моделей и
категоричная в счетной мощности, полна.
Предположим, что ни одна из формул  и
и  не выводима в теории
не выводима в теории  . Тогда обе теории
. Тогда обе теории  и
и  непротиворечивы. По
теореме 47) они имеют счетные модели, которые остаются счетными после
факторизации (перехода к нормальным моделям), поскольку
теория
непротиворечивы. По
теореме 47) они имеют счетные модели, которые остаются счетными после
факторизации (перехода к нормальным моделям), поскольку
теория  не имеет конечных моделей. Эти счетные модели должны
быть изоморфными (в силу категоричности). С другой стороны, в
одной из них истинна формула
не имеет конечных моделей. Эти счетные модели должны
быть изоморфными (в силу категоричности). С другой стороны, в
одной из них истинна формула  , а в другой —
формула
, а в другой —
формула  , так что они даже не элементарно эквивалентны
(мы знаем из раздела "Элементарная эквивалентность", что такого быть не может).
, так что они даже не элементарно эквивалентны
(мы знаем из раздела "Элементарная эквивалентность", что такого быть не может).
Аналогично доказывается и общая форма критерия Лося-Воота:
Теорема 66. Непротиворечивая теория с равенством в конечной или счетной
сигнатуре, не имеющая конечных моделей и категоричная в данной
несчетной мощности  , полна.
, полна.
Пусть теория  не полна и к ней можно присоединить без
противоречия любую из формул
не полна и к ней можно присоединить без
противоречия любую из формул  и
и  .
Рассмотрим счетные нормальные модели теорий
.
Рассмотрим счетные нормальные модели теорий 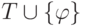 и
и  . По
теореме 62 увеличим их мощности до
. По
теореме 62 увеличим их мощности до  и получим противоречие.
и получим противоречие.
118. Условие конечности или счетности сигнатуры в этой теореме можно ослабить. Как это сделать?
Вот пример применения теоремы 66. Теория алгебраически
замкнутых полей характеристики  категорична в
любой несчетной мощности. (Это можно доказать, используя
базисы трансцендентности: такое поле имеет базис
трансцендентности над полем алгебраических чисел, мощность
которого равна мощности всего поля, а два поля с равномощными
базисами трансцендентности изоморфны). Следовательно, эта теория полна.
категорична в
любой несчетной мощности. (Это можно доказать, используя
базисы трансцендентности: такое поле имеет базис
трансцендентности над полем алгебраических чисел, мощность
которого равна мощности всего поля, а два поля с равномощными
базисами трансцендентности изоморфны). Следовательно, эта теория полна.
Заметим, что это наблюдение согласовано со знаменитой (и трудной!) теоремой Морли; эта теорема утверждает, что теория с равенством, категоричная в одной несчетной мощности, категорична и во всех несчетных мощностях. (Подробно о теореме Морли можно прочесть, например, в учебнике Кейслера и Чэна [13])
Теорема 67. Конечно аксиоматизируемая полная теория в конечной сигнатуре разрешима.
Пусть дана произвольная формула  . Будем перебирать все
выводы в исчислении предикатов и проверять, не обнаружилась ли
выводимость одной из формул
. Будем перебирать все
выводы в исчислении предикатов и проверять, не обнаружилась ли
выводимость одной из формул  или
или  из конъюнкции некоторых аксиом теории
из конъюнкции некоторых аксиом теории  . Рано или поздно одна из
них окажется выводимой (поскольку теория полна), и тем самым мы
узнаем, какая из формул выводима в теории.
. Рано или поздно одна из
них окажется выводимой (поскольку теория полна), и тем самым мы
узнаем, какая из формул выводима в теории.
Это доказательство неконструктивно в том смысле, что не дает никакой оценки на время работы алгоритма. Отметим также, что не обязательно требовать конечной аксиоматизируемости теории; достаточно, чтобы она имела разрешимое или перечислимое множество аксиом (см. [5]).
Проиллюстрируем все эти понятия на нескольких (в основном уже обсуждавшихся нами) примерах.
