Логика высказываний
Полные системы связок
Рассматриваемая нами система пропозициональных связок (  ,
, 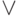 ,
, 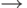 ,
,  ) полна в следующем смысле:
) полна в следующем смысле:
Теорема 3 (Полнота системы связок). Любая булева функция  аргументов может быть записана в виде
пропозициональной формулы.
аргументов может быть записана в виде
пропозициональной формулы.
Проще всего пояснить это на примере. Пусть, например, булева
функция  задана таблицей 1.4
задана таблицей 1.4

 |
 |
 |
 |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В таблице есть три строки с единицами в правой колонке — три случая,
когда булева функция истинна (равна  ). Напишем три конъюнкции,
каждая из которых покрывает один случай (а в остальных строках ложна),
и соединим их дизъюнкцией. Нужная формула построена.
). Напишем три конъюнкции,
каждая из которых покрывает один случай (а в остальных строках ложна),
и соединим их дизъюнкцией. Нужная формула построена.
Ясно, что аналогичная конструкция применима для любой таблицы (с любым числом переменных).
Для формул подобного вида есть специальное название: формулы в
дизъюнктивной нормальной форме. Более подробно: литералом называется
переменная или отрицание переменной, конъюнктом называется произвольная конъюнкция литералов,
а дизъюнктивной нормальной формой называется дизъюнкция
конъюнктов. В нашем случае в каждый конъюнкт входит  литералов (где
литералов (где  — число переменных), а число конъюнктов
равно числу строк с единицами и может меняться от нуля
(тогда, правда, получается не совсем формула, а "пустая
дизъюнкция", и ее можно заменить какой-нибудь всегда ложной
формулой типа
— число переменных), а число конъюнктов
равно числу строк с единицами и может меняться от нуля
(тогда, правда, получается не совсем формула, а "пустая
дизъюнкция", и ее можно заменить какой-нибудь всегда ложной
формулой типа 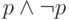 ) до
) до  (если булева
функция всегда истинна).
(если булева
функция всегда истинна).
5. Длина построенной в доказательстве теоремы 3 формулы зависит от числа единиц: формула будет короткой, если единиц в таблице мало. А как написать (сравнительно) короткую формулу, если в таблице мало нулей, а в основном единицы?
Иногда полезна конъюнктивная нормальная форма, которая представляет собой конъюнкцию дизъюнктов. Каждый дизъюнкт состоит из литералов, соединенных дизъюнкциями. Теорему 3 можно теперь усилить так:
Теорема 4. Всякая булева функция может быть выражена формулой, находящейся в дизъюнктивной нормальной форме, а также формулой, находящейся в конъюнктивной нормальной форме.
Первая часть утверждения уже доказана. Вторая часть аналогична первой, надо только для каждой строки с нулем написать подходящий дизъюнкт.
Можно также представить функцию 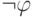 в дизъюнктивной
нормальной форме, а затем воспользоваться законами Де Моргана, чтобы внести отрицание внутрь.
в дизъюнктивной
нормальной форме, а затем воспользоваться законами Де Моргана, чтобы внести отрицание внутрь.
6. Проведите второй вариант рассуждения подробно.
Вообще говоря, определение нормальной формы не требует, чтобы в каждом конъюнкте (или дизъюнкте) встречались все переменные. (Повторять переменную больше одного раза смысла нет; если, например, переменная и ее отрицание входят в одну конъюнкцию, то эта конъюнкция всегда ложна и ее можно выбросить.)
7. Приведите пример булевой функции  аргументов, у которой любая
дизъюнктивная или конъюнктивная нормальная форма содержит лишь
члены длины
аргументов, у которой любая
дизъюнктивная или конъюнктивная нормальная форма содержит лишь
члены длины  . (Указание: рассмотрите функцию, которая меняет
свое значение при изменении значения любой переменной.)
. (Указание: рассмотрите функцию, которая меняет
свое значение при изменении значения любой переменной.)
Заметим, что при доказательстве теоремы 3 мы обошлись без импликации. Это и не удивительно, так как она выражается через дизъюнкцию и отрицание:


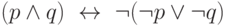
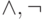 , а также система связок
, а также система связок 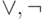 являются полными. (По определению это означает, что с их помощью
можно записать любую булеву функцию.)
являются полными. (По определению это означает, что с их помощью
можно записать любую булеву функцию.)8. Докажите, что система связок  полна.
(Указание: как записать через них дизъюнкцию?)
полна.
(Указание: как записать через них дизъюнкцию?)
А вот без отрицания обойтись нельзя. Система связок 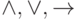 неполна — и по очень простой причине: если все
переменные истинны, то любая их комбинация, содержащая только
указанные связки, истинна. (Как говорят, все эти связки
"сохраняют единицу".)
неполна — и по очень простой причине: если все
переменные истинны, то любая их комбинация, содержащая только
указанные связки, истинна. (Как говорят, все эти связки
"сохраняют единицу".)
9. Легко понять, что любая формула, составленная только с помощью
связок  и
и 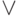 , задает монотонную булеву
функцию (в том смысле, что от увеличения значения любого из аргументов значение
функции может только возрасти — или остаться прежним). Покажите,
что любая монотонная булева функция может быть выражена формулой,
содержащей только
, задает монотонную булеву
функцию (в том смысле, что от увеличения значения любого из аргументов значение
функции может только возрасти — или остаться прежним). Покажите,
что любая монотонная булева функция может быть выражена формулой,
содержащей только  и
и 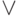 .
.
10. Пусть  — тавтология. Покажите, что найдется
формула
— тавтология. Покажите, что найдется
формула 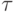 , которая включает в себя только общие для
, которая включает в себя только общие для  и
и  переменные, для которой формулы
переменные, для которой формулы 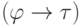 и
и  являются
тавтологиями. (Более общий вариант этого утверждения, в котором
рассматриваются формулы с кванторами, называется леммой Крейга.)
являются
тавтологиями. (Более общий вариант этого утверждения, в котором
рассматриваются формулы с кванторами, называется леммой Крейга.)
В принципе мы не обязаны ограничиваться четырьмя рассмотренными
связками. Любая булева функция может играть роль связки.
Например, можно рассмотреть связку  ,
задаваемую эквивалентностью
,
задаваемую эквивалентностью
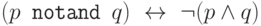
 ложно, лишь если
ложно, лишь если  и
и  истинны). Через нее выражается отрицание (
истинны). Через нее выражается отрицание (  ),
после чего можно выразить конъюнкцию, а затем, как мы знаем, и
вообще любую функцию. (Знакомые с цифровыми
логическими схемами малого уровня интеграции хорошо знакомы с этим
утверждением: достаточно большой запас схем И-НЕ позволяет реализовать
любую требуемую зависимость выхода от входов.)
),
после чего можно выразить конъюнкцию, а затем, как мы знаем, и
вообще любую функцию. (Знакомые с цифровыми
логическими схемами малого уровня интеграции хорошо знакомы с этим
утверждением: достаточно большой запас схем И-НЕ позволяет реализовать
любую требуемую зависимость выхода от входов.)Другая интересная полная система связок — сложение по
модулю 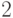 , конъюнкция и константа
, конъюнкция и константа  (которую можно
считать
(которую можно
считать  -арной связкой, задающей функцию от нуля аргументов).
Представленные в этой системе булевы функции становятся
полиномами с коэффициентами в кольце вычетов по модулю
-арной связкой, задающей функцию от нуля аргументов).
Представленные в этой системе булевы функции становятся
полиномами с коэффициентами в кольце вычетов по модулю 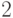 . Идея
рассматривать булевы функции как полиномы (оказавшаяся
неожиданно плодотворной в последние годы) была высказана в
1927 г. российским математиком Иваном Ивановичем
Жегалкиным.
. Идея
рассматривать булевы функции как полиномы (оказавшаяся
неожиданно плодотворной в последние годы) была высказана в
1927 г. российским математиком Иваном Ивановичем
Жегалкиным.
Назовем мономом конъюнкцию любого набора переменных или
константу  (которую естественно рассматривать как конъюнкцию
нуля переменных). Название это естественно, так как при наших
соглашениях (
(которую естественно рассматривать как конъюнкцию
нуля переменных). Название это естественно, так как при наших
соглашениях (  обозначает истину,
обозначает истину,  — ложь)
конъюнкция соответствует умножению.
— ложь)
конъюнкция соответствует умножению.
Назовем полиномом сумму таких мономов по модулю 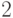 (это
значит, что
(это
значит, что 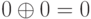 ,
,  и
и  ). Ясно, что два повторяющихся монома можно
сократить (ведь сложение по модулю
). Ясно, что два повторяющихся монома можно
сократить (ведь сложение по модулю 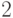 ), так что будем
рассматривать только полиномы без повторяющихся мономов.
При этом, естественно, порядок членов в мономе (как и порядок
мономов в полиноме) роли не играет, их можно переставлять.
), так что будем
рассматривать только полиномы без повторяющихся мономов.
При этом, естественно, порядок членов в мономе (как и порядок
мономов в полиноме) роли не играет, их можно переставлять.
