Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
6.2.5. Методы Якоби, Зейделя, верхней релаксации
Для системы сеточных уравнений, полученных при использовании схемы "крест"

запишем итерационный метод Якоби. Расчетные формулы (верхний индекс, как обычно, показывает номер итерации) для этого метода будут

m, l = 1, ... , M - 1, hM = 1, с условиями на сеточной границе 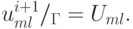
Если в явном виде выразить 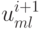 , получим каноническую форму записи сеточного метода, правую часть берем на предыдущей итерации, левую
— на текущей:
, получим каноническую форму записи сеточного метода, правую часть берем на предыдущей итерации, левую
— на текущей:

Количество итераций, требуемое для вычисления решения с точностью  оценивается по формуле
оценивается по формуле

Метод Зейделя, учитывающий результаты вычислений на i + 1 итерации, записывается для рассматриваемого уравнения Пуассона
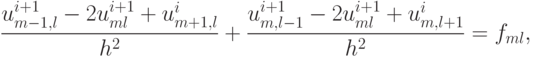
m, l = 1, ... , M - 1, hM = 1, с условиями на сеточной границе  .
.
Напомним, что хотя метод Зейделя неявный, но его реализация оказывается простой, если правильно установить последовательность вычислений. В каноническом виде формулы для метода Зейделя есть

Сначала из последнего уравнения, используя граничные условия  и
и  , находим
, находим  . Затем, зная
. Затем, зная  , можно аналогично найти
, можно аналогично найти  и так далее. Значения сеточной функции вычисляются в следующем порядке изменения индексов: (1, 1), (1, 2), ... , (1, M - 1), (2, 1), (2,
2), ... , (2, M - 1), (M - 1, 1), (M - 1, 2), ... , (M - 1, M - 1) . Оценка количества итераций, необходимых для достижения точности
и так далее. Значения сеточной функции вычисляются в следующем порядке изменения индексов: (1, 1), (1, 2), ... , (1, M - 1), (2, 1), (2,
2), ... , (2, M - 1), (M - 1, 1), (M - 1, 2), ... , (M - 1, M - 1) . Оценка количества итераций, необходимых для достижения точности  есть
есть

Метод Зейделя сходится быстрее метода Якоби, однако число итераций также оценивается как O(N2) = O(L/l) . В случае метода верхней релаксации система представляется в виде
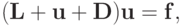
где  и
и  — нижняя и верхняя треугольные матрицы с нулевыми диагоналями,
— нижняя и верхняя треугольные матрицы с нулевыми диагоналями,  - диагональная матрица. Вводится параметр
- диагональная матрица. Вводится параметр  и итерационные формулы
записываются в виде
и итерационные формулы
записываются в виде
![$ {\mathbf{Lu}}^{i + 1} + {\mathbf{Uu}}^{i} + {\mathbf{D}} \left[\frac{{{\mathbf{u}}^{i + 1}}}{\tau}\right. + + \left. (1 - \frac{1}{\tau}){
\mathbf{u}}^{i}\right] = {\mathbf{f}} $](/sites/default/files/tex_cache/8a1b4f35735d5368140a4a7a74c6885c.png)
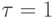 получаем метод Зейделя.
получаем метод Зейделя.Рассмотрим реализацию метода верхней релаксации для разностной аппроксимации уравнения Пуассона. Переписав разностную схему в виде

выпишем расчетные формулы для метода релаксаций:
![\begin{multline*}
\frac{u_{m - 1, l}^{i + 1} + u_{m, l - 1}^{i + 1}}{h^2} + \frac{u_{m + 1, l}^{i} + u_{m, l + 1}^{i}}{h^2} - \\
- \frac{4}{h^2} \left[\frac{u_{ml}^{i + 1}}{\tau} + (1 - \frac{1}{\tau})u^{i}_{ml}\right] =
f_{ml}, u_{ml}^{i + 1} = U_{ml}.
\end{multline*}](/sites/default/files/tex_cache/c35617b138b18ebe0b60e5baae81b057.png)
Последовательность вычислений в методе релаксаций такая же, как и в методе Зейделя. Уравнения представляются в виде
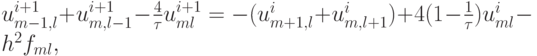
решение 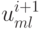 вычисляется так же с левого нижнего угла области интегрирования. Основное преимущество метода верхней релаксации перед методом
Зейделя состоит в существенном ускорении скорости сходимости при соответствующем выборе параметра
вычисляется так же с левого нижнего угла области интегрирования. Основное преимущество метода верхней релаксации перед методом
Зейделя состоит в существенном ускорении скорости сходимости при соответствующем выборе параметра 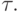 Не проводя исследований на сходимость, приведем их окончательный результат. Необходимое количество итераций
для достижения точности
Не проводя исследований на сходимость, приведем их окончательный результат. Необходимое количество итераций
для достижения точности  равно
равно

