Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 6:

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

6.2.4. Метод переменных направлений

Еще большие успехи при попытках ускорить итерационные методы были достигнуты при использовании методов переменных направлений. Можно показать, что решение нестационарной задачи

$ \frac{{\partial}u}{{\partial}t} = \frac{{{\partial}^2 u}}{{{\partial}x^2}} + \frac{{{\partial}^2 u}}{{{\partial}y^2}} - f, \quad $

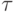со стационарными граничными условиями \left. u\right|_\Gamma = \varphi будет стремиться к некоторому стационарному пределу при t \longrightarrow \infty или при n \longrightarrow \infty. В этом пункте n — количество шагов по времени при решении рассматриваемого дифференциального уравнения в частных производных разностным методом. В этом случае итерационный параметр \tau играет роль шага по времени, отличие состоит лишь в том, что итерационный параметр не обязан быть малым, хорошая аппроксимация нестационарного уравнения не требуется.

Представим метод переменных направлений в следующем виде:

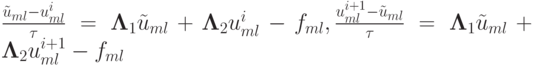
$ \frac{{\tilde{u}_{ml} - u_{ml}^{i}}}{\tau} = {\mathbf{\Lambda}}_1 \tilde{u}_{ml} + {\mathbf{\Lambda}}_2 u_{ml}^{i} - f_{ml}, \frac{{u_{ml}^{{i} + 1} - \tilde{u}_{ml}}}{\tau} = {\mathbf{\Lambda}}_1 \tilde{u}_{ml} + {\mathbf{\Lambda}}_2 u_{ml}^{{i} + 1} - f_{ml} $

Уравнение для эволюции погрешности получается, если из приведенных формул вычесть тождество

$ \frac{{u_{ml} - u_{ml}}}{\tau} = {\mathbf{\Lambda}}_1 u_{ml} + {\mathbf{\Lambda}}_2 u_{ml} - f\colon \quad \quad \frac{{\tilde{r}_{ml} - r_{ml}^{i}}}{\tau} = {\mathbf{\Lambda}}_1 \tilde{r}_{ml} + {\mathbf{\Lambda}}_2 r_{ml}^{i}, \frac{{r_{ml}^{{i} + 1} - \tilde{r}_{ml}}}{\tau} = {\mathbf{\Lambda}}_1 \tilde{r}_{ml} + {\mathbf{\Lambda}}_2 r_{ml}^{{i} + 1} . $

Представим rml и $ \tilde{r}_{ml} $ в виде разложения по базису из собственных функций:

r_{ml}^{i} = \sum\limits_{{p} \cdot {q}}{c_{pq}^{i} {\Psi}_{ml}^{pq}} ; \tilde{r}_{ml} = \sum\limits_{{p}{q}}{\tilde{c}_{pq} {\Psi}_{ml}^{pq}}

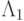и рассмотрим эволюцию погрешности за одну итерацию. {\Psi}^{pq}, как и ранее, собственные векторы разностных операторов \Lambda_1 и \Lambda _{2}, cpq — коэффициенты Фурье ; невязка r_{ml}^{i} обращается в нуль на границах области интегрирования.

Используя разностное уравнение для $ \tilde{r}_{ml} $ представим связь между невязкой на предыдущей итерацией и невязкой на промежуточном слое в виде

(\mathbf{E} -{\tau}\Lambda_1) \tilde{r}_{ml} = (\mathbf{E} +{\tau}\Lambda_2) r_{ml}^{i}.

Используя представление Фурье, получим

({\mathbf{E}} -{\tau}{\mathbf{\Lambda}}_1 ) \sum\limits_{pq}{\tilde{c}_{pq}} {\Psi}_{ml}^{pq} = ({\mathbf{E}} + \tau {\mathbf{\Lambda}}_2 ) \sum\limits_{pq} {c_{pq}^{i}} {\Psi}_{ml}^{pq},

откуда после действия операторов \Lambda _{1} и \Lambda _{2} на суммы, получаем

\sum\limits_{pq} \tilde{c}_{pq} (1 +{\tau}\lambda^{p}) {{\Psi}}^{pq} = \sum\limits_{pq} c_{pq}^{i} (1 -{\tau}\lambda^{p}) {\Psi}^{pq}.

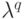Здесь \lambda ^{p} и \lambda ^{q} — собственные значения разностных операторов \Lambda _{1} и \Lambda_2 (0 < l \le {\lambda}^{p}, 0 < {\lambda}^{q} \le L, l \approx \pi^2, L \approx 4N^2), N — число шагов по каждому пространственному измерению рассматриваемой системы разностных уравнений. В силу единственности разложения сеточной функции по базису {\Psi}^{pq}, получаем соотношение для коэффициентов Фурье

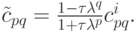
$ \tilde{c}_{pq} = \frac{{1 -{\tau}{\lambda}^{q}}}{{1 + \tau {\lambda}^{p}}}c_{pq}^{i}. $

Аналогично, после спектрального анализа второго этапа расчета, получим

$ c_{pq}^{i + 1} = \frac{{1 -{\tau}{\lambda}^{p}}}{{1 + \tau {\lambda}^{q}}} \tilde{c}_{pq} = \frac{{1 -{\tau}{\lambda}^{p}}}{{1 +{\tau}{\lambda}^{q}}} \frac{{1 -{\tau}{\lambda}^{q}}}{{1 +{\tau}{\lambda}^{p}}} c_{pq}^{i} $

Введем обозначение

$ {\mu}(\tau) = \max\limits_{{\lambda}\in [l, L]} | \frac{1 -{\tau}\lambda}{1 + \tau \lambda}|, $

тогда для коэффициентов разложения справедливо неравенство 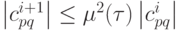\left|{c_{pq}^{i + 1}}\right| \le {\mu}^2 ({\tau}) \left| {c_{pq}^{i}}\right|, следовательно, для нормы невязки имеем условие \left\| {\mathbf{r}^{i + 1}}\right\| \le {\mu}^2 ({\tau}) \left\| {\mathbf{r}^{i}}\right\|, так как \left\|{\mathbf{r}^{i + 1}}\right\| = \left\| \sum {c^{i + 1}_{pq} {\Psi}^{pq}}\right\| \le \| \sum {{\mu}^2 c^{i}_{pq} {\Psi}^{pq}}\| \le {\mu}^2 \| \sum{c^{i + 1}_{pq} {\Psi}^{pq}}\| = {\mu}^2 \|\mathbf{r}^{i}\|, поскольку справедливо равенство Парсеваля. 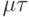Необходимо обеспечить наиболее быструю сходимость, минимизировав коэффициент \mu \tau.

Найдем оптимальное значение параметра 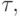\tau, обеспечивающее \min\limits_{\tau}{\mu}({\tau}). Для этого необходимо решить задачу

${\tau} = \arg \left\{{\min\limits_{\tau}\left[{\max\limits_{{\lambda}\in \left[{l, L}\right]} \left| {\frac{{1 -{\tau}{\lambda}}}{{1 +{\tau}\lambda}}}\right|}\right]}\right\}, $

которая решается так же, как и ранее. Простой графический анализ функции

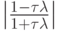
$ \left| {\frac{{1 -{\tau}{\lambda}}}{{1 +{\tau}{\lambda}}}}\right| $
приводит к результату
$ \max\limits_{{\lambda}\in [l, L]} \left| {\frac{{1 - \tau {\lambda}}}{{1 +{\tau}{\lambda}}}}\right| = \max\limits_{{\lambda} \in [l, L]} \left\{{\left| {\frac{{1 -{\tau}l}}{{1 +{\tau}l}}}\right| , \left| {\frac{{1 -{\tau}L}}{{1 +{\tau}L}}}\right|}\right\} $
.

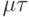Минимум \mu \tau достигается, как и в предыдущем случае, при

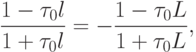
\frac{1 - \tau_0 l}{1 + \tau_0 l} = - \frac{1 - \tau_0 L}{1 + \tau_0 L} ,
откуда сразу получается 2 = 2 \tau_0^2 lL, \tau_0 = 1/{\sqrt{lL}}.

Вычислим значение

$ {\mu}(\tau_0 ) = \frac{{1 - l/ \sqrt{lL}}}{{1 + l/ \sqrt{lL}}} \approx 1 - 2 \sqrt{l/L} . $
Погрешность за одну двухэтапную итерацию убывает, таким образом, в q = {\mu}^2 \approx 1 - 4 \sqrt{l/L} раз, l \ll L.

Количество итераций, необходимое для достижения заданной точности, можно оценить как

$ i \approx \frac{\ln {\varepsilon}^{- 1}}{4 \sqrt{l/L}} = \frac{1}{4} \sqrt{\frac{L}{l}} \ln {\varepsilon}^{- 1} . $

Скорость сходимости итерационного процесса для приведенного метода приблизительно такая же, как и для процесса с чебышевским набором итерационных параметров. Эти результаты могут быть сформулированы в виде теоремы.

Естественным обобщением приведенного итерационного процесса представляется замена одного итерационного параметра 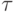\tau набором \tau _{i}. Выбор этих параметров приводит к минимаксной задаче

$ \min\limits_{\tau}\left\{\max\limits_{{\lambda}\in \left[{l, L}\right]} \prod\limits_{j = 1}^{i}{\left| {\frac{{1 - \tau_j {\lambda}}}{{1 + \tau_j {\lambda}}}}\right|^2}}\right\}, $

решение которой представляется в виде громоздкого алгоритма, который здесь не приводится. Для этого метода имеем оценку числа итераций для достижения заданной точности i \approx \ln {\varepsilon}^{- 1} \ln {L/l}.

Дальше >>
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

Вопросы и ответы

вопросов: 0