Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 3:

Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

3.4. Численные методы решения уравнений в частных производных гиперболического типа для квазилинейного уравнения переноса

Рассмотрим теперь простейшие разностные схемы для уравнения Хопфа.

Обобщение на случай уравнения Хопфа схемы П.Лакса имеет вид

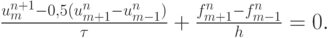
$ \frac{{u_m^{n + 1} - 0, 5(u_{m + 1}^{n} - u_{m - 1}^{n})}}{\tau} + \frac{{f_{m + 1}^{n} - f_{m - 1}^{n}}}{h} = 0. $

Здесь, очевидно, используется дивергентный вид уравнения (3.6).

Упражнения. Рассмотрим схему Лакса - Вендроффа для уравнения Хопфа. Пусть начальные условия для задачи Коши поставлены следующим образом: u(x, 0) = ch - 2(x). Тогда уравнение Хопфа имеет первый интеграл: \int\limits_{- \infty }^{+ \infty }{u({x, t})dx} = {const}. Проверить, что приведенная выше схема является консервативной, т.е. в ней на сеточном уровне автоматически выполняется тот же закон сохранения.

Построить аналогичную схему с использованием характеристической формы записи уравнения Хопфа (3.9). Будет ли она консервативной?

Схема условно устойчива при выполнении условия Куранта (точнее, обобщения условия Куранта)

$ \frac{\tau}{h} \max\limits_m \left| {u_m^{n}} \right| \le 1. $
Здесь и ниже, как и ранее в (3.7), f = 0, 5u2 . При этом предполагается, что течение достаточно гладкое, момент градиентной катастрофы еще не наступил, в решении нет ударных волн и других разрывов.

Схема Куранта - Изаксона - Риса. Обобщение схем КИР на квазилинейный случай (при использовании дивергентной формы записи уравнений) очевидно.

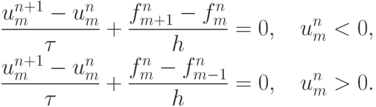
\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{f_{m + 1}^{n} - f_m^{n}}}{h} = 0, \quad u_m^{n} < 0, \\ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{f_m^{n} - f_{m - 1}^{n}}}{h} = 0, \quad u_m^{n} > 0. \end{gather*}

Схема устойчива при выполнении условия Куранта

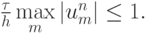
$ \frac{\tau}{h} \max\limits_m \left| {u_m^{n}}\right| \le 1. $

Обобщение схемы Лакса - Вендроффа (схема предиктор - корректор). Для квазилинейных уравнений (а также линейных уравнений с переменными коэффициентами, неоднородных уравнений и т.п.) схема Лакса - Вендроффа становится более сложной. Для ее построения необходимо ввести так называемые полуцелые точки (точки с дробными индексами). На первом этапе (предиктора) значения в полуцелых точках вычисляются по приведенной выше схеме — обобщению на квазилинейный случай схемы Лакса:

\begin{gather*} \frac{{u_{m + 1/2}^{n + 1/2} - 0, 5(u_{m + 1}^{n} + u_m^{n})}}{{{\tau}/2}} + \frac{{f_{m + 1}^{n} - f_m^{n}}}{h} = 0, \\ \frac{{u_{m - 1/2}^{n + 1/2} - 0, 5(u_m^{n} + u_{m - 1}^{n})}}{{{\tau}/2}} + \frac{{f_m^{n} - f_{m - 1}^{n}}}{h} = 0, \end{gather*}

на втором этапе (корректор) используется схема "чехарда" (трехслойная схема на крестообразном шаблоне, которая не входит в семейство (3.8)):

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{f_{m + 1/2}^{n + 1/2} - f_{m - 1/2}^{n + 1/2}}}{h} = 0. $

Схема Лакса - Вендроффа принадлежит к так называемым центральным схемам. Ее шаблон симметричен. На первом этапе рассчитываются значения сеточной функции в полуцелых точках шаблона на промежуточном слое (tm - 1/2, xm - 1/2), (tn + 1/2, xm + 1/2), на втором этапе вычисляется решение на верхнем слое в точке (tn + 1, xm). Схема устойчива при выполнении условия Куранта.

Аналогично строятся схемы Лакса - Вендроффа для линейных неоднородных уравнений.

Нецентральная схема Мак - Кормака (предиктор - корректор).

Как и приведенная выше схема Лакса - Вендроффа, схема МакКормака состоит из двух этапов. Рассмотрим построение схемы МакКормака для однородного уравнения (3.7). Первый этап (предиктор) имеет вид

\begin{gather*} \frac{{\tilde{u}_m - u_m^{n}}}{\tau} + \frac{{f_{m + 1}^{n} - f_m^{n}}}{h} = 0, \\ \frac{{\tilde{u}_{m - 1} - u_m^{n}}}{\tau} + \frac{{f_m^{n} - f_{m - 1}^{n}}}{h} = 0, \end{gather*}

т.е. используется схема "явный правый уголок". Второй этап — корректор:

$ \frac{{u_m^{n + 1} - 0, 5(u_m^{n} + \tilde{u}_m )}}{\tau} + \frac{{\tilde{f}_m - \tilde{f}_{m - 1}}}{2h} = 0. $

Таким образом, расчет на первом этапе по схеме "правый уголок", на втором — "левый уголок".

Другая схема Мак - Кормака имеет вид

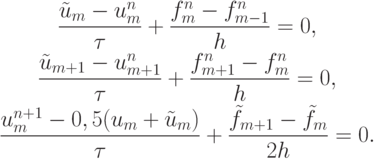
\begin{gather*} \frac{{\tilde{u}_m - u_m^{n}}}{\tau} + \frac{{f_m^{n} - f_{m - 1}^{n}}}{h} = 0, \\ \frac{{\tilde{u}_{m + 1} - u_{m + 1}^{n}}}{\tau} + \frac{{f_{m + 1}^{n} - f_m^{n}}}{h} = 0, \\ \frac{{u_m^{n + 1} - 0, 5(u_m + \tilde{u}_m )}}{\tau} + \frac{{\tilde{f}_{m + 1} - \tilde{f}_m }}{2h} = 0. \end{gather*}

Такие разностные схемы называют нецентральными. К их преимуществам относят отсутствие полуцелых индексов, более простую постановку граничных условий. В линейном случае схемы Мак - Кормака совпадают со схемой Лакса - Вендроффа. Схемы имеют второй порядок аппроксимации по обеим переменным, схемы устойчивы при выполнении условия Куранта.

Схема Русанова (центральная схема третьего порядка точности).

Для построения схемы Русанова вводятся не только полуцелые точки, но и два слоя промежуточных точек с дробными индексами. Первый этап схемы Русанова (переход к слою 1/3) имеет вид

\begin{gather*} \frac{u_{m + 1/2}^{n + 1/3} - 0, 5(u_m^{n} + u_{m + 1}^{n})}{{\tau}/3} + \frac{{f_{m + 1}^{n} - f_m^{n}}}{h} = 0, \\ \frac{{u_{m - 1/2}^{n + 1/3} - 0, 5(u_m^{n} + u_{m - 1}^{n})}}{{\tau}/3} + \frac{{f_m^{n} + f_{m - 1}^{n}}}{h} = 0, \end{gather*}

ее второй этап есть схема "чехарда"

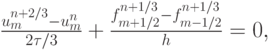
$ \frac{u_m^{n + 2/3} - u_m^n}{2{\tau}/3} + \frac{f_{m + 1/2}^{n + 1/3} - f_{m - 1/2}^{n + 1/3}}{h} = 0, $

а третий этап

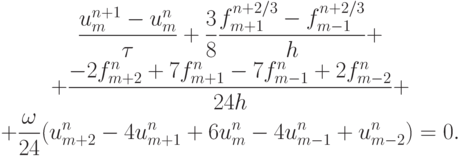
\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{3}{8} \frac{{f_{m + 1}^{n + 2/3} - f_{m - 1}^{n + 2/3}}}{h} + \\ + \frac{- 2f_{m + 2}^n + 7f_{m + 1}^n - 7f_{m - 1}^n + 2f_{m - 2}^n}{24h} + \\ + \frac{\omega }{{24}}(u_{m + 2}^{n} - 4u_{m + 1}^{n} + 6u_m^{n} - 4u_{m - 1}^{n} + u_{m - 2}^{n}) = 0. \end{gather*}

На первом этапе производится расчет по схеме Лакса, на втором — по схеме "крест" ("чехарда"). Последнее слагаемое третьего этапа вводится для обеспечения устойчивости схемы (член, пропорциональный разностной аппроксимации 4 - й производной).

Схема является условно устойчивой при выполнении условия Куранта и условия 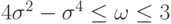4{\sigma}^2 - {\sigma}^4 \le \omega \le 3.

Нецентральная схема Уорминга - Кутлера - Ломакса 3 - го порядка точности.

Первый этап:

\begin{gather*} \frac{u_m^{n + 1/3} - u_m^n}{2{\tau}/3} + \frac{f_{m + 1}^n - f_m^n}{h} = 0, \\ \frac{u_{m - 1}^{n + 1/3} - u_{m - 1}^n}{2{\tau}/3} + \frac{f_m^n - f_{m - 1}^n}{h} = 0, \end{gather*}

Второй этап:

\begin{gather*} \frac{u_m^{n + 2/3} - 0, 5(u_m^{n} + u_m^{n + 1/3})}{2{\tau}/3} + \frac{f_m^{n + 1/3} - f_{m - 1}^{n + 1/3}}{2h} = 0, \\ \frac{u_{m + 1}^{n + 2/3} - 0, 5(u_{m + 1}^{n} + u_{m + 1}^{n + 1/3})}{2{\tau}/3} + \frac{f_{m + 1}^{n + 1/3} - f_m^{n + 1/3}}{2h} = 0, \end{gather*}

Третий этап:

\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{3}{8} \cdot \frac{{f_{m + 1}^{n + 1/3} - f_{m - 1}^{n + 1/3}}}{h} + \\ + \frac{- 2f_{m + 2}^n + 7f_{m + 1}^n - 7f_{m - 1}^n + 2f_{m - 2}^n}{24h} + \\ + \frac{\omega }{24}(u_{m + 2}^{n} - 4u_{m + 1}^{n} + 6u_m^{n} - 4u_{m - 1}^{n} + u_{m - 2}^{n}) = 0. \end{gather*}

Последний член добавляется для устойчивости схемы, которая является условно устойчивой при выполнении условий Куранта.

Неявная схема Бима - Уорминга.

Схема Бима - Уорминга имеет вид:

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{1}{2} \left[{\frac{{\partial}f}{{\partial}x}(t^{n}, x_m ) + \frac{{\partial}f}{{\partial}x}(t^{n + 1}, x_m )}\right] = 0. $

Рассмотрим алгоритм расчетов по схеме Бима - Уорминга. Линеаризуем функцию 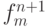f_m^{n + 1}:

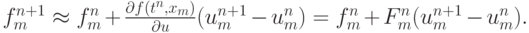
$ f_m^{n + 1} \approx f_m^{n} + \frac{{{\partial}f(t^{n}, x_m )}}{{\partial}u}(u_m^{n + 1} - u_m^{n}) = f_m^{n} + F_m^{n} (u_m^{n + 1} - u_m^{n}). $

Здесь мы воспользовались тем, что функция f не зависит явно от времени, иначе формулы будут выглядеть несколько иначе. Тогда будем иметь равенство

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{1}{2} \left\{{2 \frac{{{\partial}f(t^{n}, x_m )}}{{\partial}u} + \frac{{\partial}}{{\partial}x}[F_m^{n} (u_m^{n + 1} - u_m^{n})]}\right\} = 0. $

Проведя аппроксимацию производной ({\partial}f/ \partial x)_m^{n} центральными разностями, получим искомую неявную разностную схему:

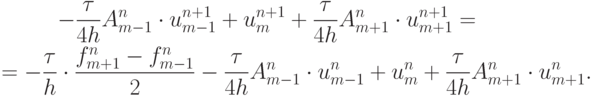
\begin{gather*} - \frac{\tau}{{4h}}A_{m - 1}^{n} \cdot u_{m - 1}^{n + 1} + u_m^{n + 1} + \frac{\tau}{{4h}}A_{m + 1}^{n} \cdot u_{m + 1}^{n + 1} = \\ = - \frac{\tau}{h} \cdot \frac{{f_{m + 1}^{n} - f_{m - 1}^{n}}}{2} - \frac{\tau}{{4h}}A_{m - 1}^{n} \cdot u_{m - 1}^{n} + u_m^{n} + \frac{\tau}{{4h}}A_{m + 1}^{n} \cdot u_{m + 1}^{n}. \end{gather*}

В результате для аппроксимации уравнения Хопфа получается система линейных алгебраических уравнений с трехдиагональной матрицей, алгоритм численного решения которой — один из вариантов трехточечной прогонки.

Дальше >>
< Лекция 2 || Лекция 3: 1234567891011 || Лекция 4 >

Вопросы и ответы

вопросов: 0