Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1276 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы

Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности

A
|
версия для печати
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

2.2. Разностные схемы для численного решения нелинейного уравнения теплопроводности

2.2.1. Неявная схема с нелинейностью на нижнем слое

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \frac{1}{h} \left[{a_{n + 1\2} \frac{u_{m + 1}^{n + 1} - u_m^{n + 1}}{h} - a_{n - 1\2}} \frac{u_m^{n + 1} - u_{m - 1}^{n + 1}}{h}}\right] + f_m^{n}, $

где am + 1/2 вычисляется следующим образом:

  1. $ a_{m + 1/2} = \frac{1}{2}(a(u_m^{n} ) + a(u_{m + 1}^{n} )), $
  2. $ a_{m + 1/2} = a \left({\frac{{u_m^{n} + u_{m + 1}^{n}}}{2}}\right), $
  3. $ a_{m + 1/2} = a \left({\frac{{2u_m^{n}u_{m + 1}^{n}}}{{u_m^{n} + u_{m + 1}^{n}}}}\right), $
  4. $ a_{m + 1/2} = \frac{{2a(u_m^{n} ) a(u_{m + 1}^{n})}}{{a(u_m^{n} ) + a(u_{m + 1}^{n} )}}. $

На верхнем слое по времени решение находится с помощью метода прогонки. Недостаток схемы заключается в необходимости выполнения условия, ограничивающего шаг по времени: \tau \left\| {f^{\prime}_u}\right\| \ll 1.

2.2.2. Схема с нелинейностью на верхнем слое

(необходимость ее реализации появляется, когда условие {\tau}\left\|{f^{\prime}_u}\right\| \ll 1 оказывается трудновыполнимым):

$ \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} = \frac{1}{h} \left({a_{m + 1/2}^{n + 1}\frac{{u_{m + 1}^{n + 1} - u_m^{n + 1}}}{h} - a_{m - 1/2}^{n + 1} \frac{{u_m^{n + 1} - u_{m - 1}^{n + 1}}}{h}}\right) + f_m^{n + 1}. $

Для реализации алгоритма прогонки проведем линеаризацию функции в правой части, то есть используем итерационный метод Ньютона в функциональных пространствах (метод квазилинеаризации). Пусть u_m^{i} есть i приближение к u_m^{n + 1} ; необходимо вычислить u_m^{n + 1}.

Тогда

\begin{gather*} f(u_m^{i + 1} ) = f[u_m^{i} + (u_m^{i + 1} - u_m^{i} )] \approx f(u_m^{i} ) + f^{\prime}_u (u_m^{i} ) (u_m^{i + 1} - u_m^{i} ), \\ a(u_m^{i + 1} ) = a[u_m^{i} + (u_m^{i + 1} - u_m^{i} )] \approx a (u_m^{i} ) + a^{\prime}_u (u_m^{i} ) (u_m^{i + 1} - u_m^{i} ). \end{gather*}

Для вычисления значений сеточной функции на следующем временном слое имеем СЛАУ с трехдиагональной матрицей:

\begin{gather*} \frac{{u_m^{i + 1} - u_m^{n}}}{\tau} = \frac{1}{h} \left({a_{m + 1/2}^{i} \frac{{u_{m + 1}^{i + 1} - u_m^{i + 1}}}{h} - a_{m - 1/2}^{i} \frac{{u_m^{i + 1} - u_{m - 1}^{i + 1}}}{h}}\right) + \\ + f(u_m^{i} ) + f^{\prime}_u (u_m^{i} )(u_m^{i + 1} - u_m^{i} ). \end{gather*}

Итерации продолжаются до выполнения условия

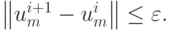
\left\| {u_m^{i + 1} - u_m^{i}}\right\| \le \varepsilon.

При реализации шеститочечной схемы с переменным коэффициентом теплопроводности и нелинейной правой частью f(u) итерационный процесс может иметь следующий вид:

\begin{gather*} \frac{{u_m^{i + 1} - u_m^{n}}}{\tau} - \frac{1}{{2h}} \left[{\left({a_{i + 1/2}^{n} \frac{{u_{m + 1}^{i + 1} - u_m^{i + 1}}}{h} - a_{i - 1/2}^{n} \frac{{u_m^{i + 1} - u_{m - 1}^{i + 1}}}{h}}\right)}\right. + \\ + \left. {\left({a_{i + 1/2}^{n} \frac{{u_{m + 1}^{n} - u_m^{n}}}{h} - a_{n - 1/2}^{n} \frac{{u_m^{n} {- } u_{m - 1}^{n}}}{h}}\right)}\right] = f(u_m^{i} ) + f^{\prime}_u (u_m^{i} )(u_m^{i + 1} - u_m^{i} ). \end{gather*}

Здесь также была применена линеаризация функции f(u).

Отдельно рассмотрим важный частный случай a = uk. В довольно грубом приближении уравнение описывает тепловые волны, образующиеся в высокотемпературной плазме и при образовании сверхновых звезд.

$ \frac{{\partial}u}{{\partial}t} = \frac{{\partial}}{{\partial}x}(u^{k} \frac{{\partial}u}{{\partial}x}). $

Начальное условие для этой задачи u(x, 0) = 0, граничные условия —

u(0, t) = C t^{1 \over k}, \lim\limits_{x \to + \infty } u({x, t}) = 0.

Будем искать автомодельное решение задачи, т.е. решение, зависящее не от двух переменных t и x, а от одной, являющейся их комбинацией:

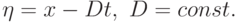
\eta = x - Dt,\ D = const.

Часто под автомодельными понимают решения, зависящие от безразмерных комбинаций независимых переменных. Введенную переменную иногда называют переменной бегущей волны. В этом случае

$ \frac{{\partial}u}{{\partial}t} = \frac{du}{{d \eta }} \cdot \frac{{{\partial}\eta }}{{\partial}t} = - D \frac{du}{{d \eta }}, \frac{{\partial}u}{{\partial}x} = \frac{{\partial}u}{{{\partial}\eta }}, $

тогда рассматриваемое уравнение приобретает вид

- Du' = (uk u')'.

Штрихом здесь обозначено дифференцирование по новой переменной \eta. Скорость распространения волны, обозначенная здесь через D, будет определена ниже. После интегрирования обыкновенного дифференциального уравнения получим

- Du = u^{k} \cdot u^{\prime}_{\eta}.

Постоянную интегрирования полагаем равной нулю, так как должно выполняться условие непрерывности теплового потока на фронте тепловой волны. Далее

- D = u^{k - 1} \cdot u^{\prime},

или (u^{k})'_{\eta } = - kD, откуда u^{k}(\eta ) = - kD \eta или u(\eta ) = \sqrt[k]{{kD}} \cdot (- \eta )^{1/k}.

Интересуют только положительные решения при \eta \ge 0, т.е. при x \le {Dt}. При \eta > 0 положим u(\eta ) = 0. В таком случае обобщенное решение (так как в точке \eta = 0 получается разрыв первой производной) рассматриваемой задачи будет иметь вид

u(\eta ) = \left\{ \begin{array}{cc} \sqrt[k]{kD(- \eta ) }, & \eta < 0 \\ 0, & \eta > 0. \\ \end{array} \right.

Скорость фронта тепловой волны легко определяется из граничного условия:

D = \sqrt{C^{k}/k}.

Квазилинейное уравнение вида

$ \frac{{\partial}u}{{\partial}t} = \frac{{\partial}}{{\partial}x} (a_0 u^{k} \frac{{\partial}u}{{\partial}x}) + q_0u^{l} $

имеет качественно различные решения при разных параметрах k и l. Но в окрестности теплового фронта при распространении тепла по нулевому фону все эти решения имеют одинаковую асимптотику, решения в окрестности фронта устроены так же, как и у рассмотренной выше задачи о распространении тепловой волны.

Дальше >>
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Вопросы и ответы

вопросов: 0