Основы машинной графики
Однородное представление двумерной точки (x,y) в общем случае имеет вид (wx wy w), где w - любой ненулевой скаляр, иногда называемый множителем. При этом если для точки задано ее представление в однородных координатах P(x y w), то найти ее двумерные координаты можно поделив первые две на скалярный множитель (x/w y/w). Вообще двумерное представление точки (x y w) есть ее проекция на плоскость w=1 (рис. 1.6).
Теперь точки плоскости можно описывать трехэлементным вектором, а матрицы преобразования должны иметь размер 3х3. В общем случае преобразование точки (x,y) в новую точку (x',y') можно представить следующим образом  .
.
Уравнения переноса (сдвига), масштабирования и вращения записываются в виде матриц преобразования однородных координат следующим образом:
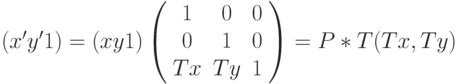
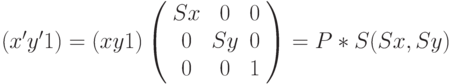

где Tx,Ty - величины сдвига, Sx,Sy - масштабные множители,  - угол поворота.
- угол поворота.
Преимущество такого подхода (матричных формул) заключается в том, что совмещение последовательных элементарных преобразований при этом значительно упрощается. Рассмотрим следующую последовательность преобразований: масштабирование исходной точки P(x,y) при масштабных коэффициентах Sx и Sy, а затем смещение ее (после масштабирования) на Tx и Ty. Запишем преобразования масштабирования и переноса (сдвига) через однородные координаты точки:

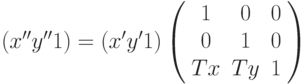
Подставим первое уравнение во второе:

В результате получим
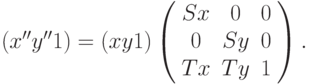
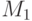 и
и  представляют собой матрицы элементарных преобразований, то существует две возможные композиции:
представляют собой матрицы элементарных преобразований, то существует две возможные композиции:  и
и  . Однако, результаты таких преобразований будут различны, в силу того, что произведение матриц не является коммутативной операцией. Если геометрический объект состоит из большого количества вершин (точек), то с вычислительной точки зрения гораздо более эффективнее и проще применять композитную (результирующую) матрицу преобразования вместо того, чтобы последовательно использовать ("умножать на") одну за другой элементарные матрицы.
. Однако, результаты таких преобразований будут различны, в силу того, что произведение матриц не является коммутативной операцией. Если геометрический объект состоит из большого количества вершин (точек), то с вычислительной точки зрения гораздо более эффективнее и проще применять композитную (результирующую) матрицу преобразования вместо того, чтобы последовательно использовать ("умножать на") одну за другой элементарные матрицы.До сих пор мы рассматривали преобразования как перевод множества точек, принадлежащих объекту, в некоторое другое множество точек, причем оба эти множества описаны в одной и той же системе координат. Другими словами система координат у нас оставалась неизменной, а сам объект преобразовывался относительно начала координат. Эквивалентным способом описания преобразования является смена системы координат. Такой подход оказывается полезным и удобным, когда необходимо собрать вместе много объектов, каждый из которых описан в своей собственной локальной системе координат, и выразить (пересчитать) их координаты в одной глобальной (мировой) системе координат. Например, точка на рис. 1.7 описана в четырех системах координат, и имеет соответствующие координаты: (11,10), (8,8), (12,10), (3,3)
Преобразование из системы координат 1 в систему координат 2 есть  ; из 2 в 3 есть
; из 2 в 3 есть  ; из 3 в 4 есть
; из 3 в 4 есть 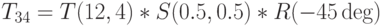 . В общем случае преобразование
. В общем случае преобразование  переводит оси системы координат j в оси системы координат i. Если
переводит оси системы координат j в оси системы координат i. Если 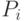 - точка, координаты которой заданы в системе координат j, то будет справедлива запись
- точка, координаты которой заданы в системе координат j, то будет справедлива запись  . Так, например, в рассматриваемом случае
. Так, например, в рассматриваемом случае  записывается в однородных координатах
записывается в однородных координатах  , а
, а 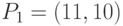 . И преобразование будет иметь вид:
. И преобразование будет иметь вид:

 имеет обратное
имеет обратное  - преобразование из системы координат 2 в систему 1, причем
- преобразование из системы координат 2 в систему 1, причем  . В рассматриваемом случае
. В рассматриваемом случае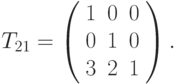
 (единичная матрица). Кроме того будет справедливо и такое выражение
(единичная матрица). Кроме того будет справедливо и такое выражение  . Другими словами, преобразование из системы координат 1 в систему координат 3 есть произведение двух матриц, первая из которых описывает преобразование из системы 1 в систему 2, а вторая – из системы 2 в систему 3.
. Другими словами, преобразование из системы координат 1 в систему координат 3 есть произведение двух матриц, первая из которых описывает преобразование из системы 1 в систему 2, а вторая – из системы 2 в систему 3.Для введения трехмерной декартовой системы координат проведем три направленные взаимно перпендикулярные прямые линии, называемые осями, так чтобы они пересекались в одной точке – начале координат. Выберем на осях единицу измерения. Тогда положение любой точки пространства можно описать через координаты этой точки, которые представляют собой расстояния от начала координат до проекций точки на соответствующие оси. Такая система координат называется ортогональной. Таким образом, положение точки P в пространстве описывается ее координатами: P=(x,y,z). Взаимное расположение координатных осей в ортогональной системе трехмерного пространства может быть двух видов. При добавлении третьей оси к двумерной системе координат ось Oz можно направить как от наблюдателя в плоскость листа, так и от плоскости листа к наблюдателю.
В первом случае систему координат принято называть левосторонней, во втором – правосторонней. Известен способ определения типа системы по ладоням. Так для левой ладони большой (ось Y), указательный (ось Z) и средний (ось X) пальцы образуют левую тройку ортогональных векторов.
В трехмерном пространстве значительно возрастает разнообразие геометрических объектов. При работе на двумерной плоскости мы рассматривали отрезки, плоские кривые и многоугольники. При переходе в трехмерное пространство это многообразие примитивов можно рассматривать в разных плоскостях, а также здесь появляются пространственные кривые: ![\rho (t)=[x(t),y(t),z(t)], t \in [a,b]](/sites/default/files/tex_cache/88fd36240c07364775f5878052bded33.png) . Помимо всего прочего в трехмерном пространстве присутствуют пространственные объекты – участки криволинейных поверхностей и объемные тела – параллелепипеды, эллипсы, тетраэдры и др.
. Помимо всего прочего в трехмерном пространстве присутствуют пространственные объекты – участки криволинейных поверхностей и объемные тела – параллелепипеды, эллипсы, тетраэдры и др.
При работе в трехмерном пространстве возникает проблема описания формы объектов. На практике получили широкое распространение три основных типа моделей трехмерных объектов: описание объекта поверхностями, сплошными телами и с помощью проволочной сетки. При первом подходе объект представляется в виде тонких поверхностей, под которым находится пустое незаполненное пространство. Примером такого объекта может выступать неразбитая скорлупа совершенно пустого внутри яйца. Поверхность объекта может быть описана различными математическими моделями. Поверхности, заданные в виде x=x(u,v),y=y(u,v),z=z(u,v), где u,v - параметры, изменяющиеся в заданных пределах, относятся к классу параметрических. Для одной фиксированной пары значений u,v можно вычислить положение только одной точки поверхности. Для полного представления всей поверхности необходимо с определенным шагом перебрать множество пар u,v из диапазона их изменений, вычисляя для каждой пары значение XYZ в трехмерном пространстве. Очень широкое распространение получили параметрические бикубические поверхности, с помощью которых достигается непрерывность составной функции и ее первых производных (функция, составленная из нескольких смежных бикубических участков, будет обладать непрерывностью и гладкостью в местах стыковки). Основным преимуществом параметрического описания является возможность построения объекта с очень сложной и замысловатой формой. Недостатком такого способа описания являются большие вычислительные затраты при построении поверхностей. Частным случаем параметрических поверхностей являются поверхности первого порядка. Из таких поверхностей можно составить описание формы объекта типа полигонального поля. Такими полями называют серию смежных многоугольников, не имеющих разрывов между собой. Каждое ребро такого поля является общим для смежных многоугольников. В результате чего составная функция, описывающая поверхность, обладает непрерывностью, а производная имеет разрывы в местах стыка участков поверхностей. В настоящее время полигональный способ описания трехмерных объектов является одним из самых распространенных и востребованных. Так, например, производительность современных графических процессоров (видеокарт) определяется количеством выводимых полигонов в единицу времени, как правило, в секунду.
Еще один способ описания поверхностей, который следует упомянуть, заключается в представлении формы объекта множеством отдельных точек, принадлежащих этой поверхности. Теоретически при бесконечном увеличении числа точек такая модель обеспечивает непрерывную форму описания. Точки, используемые для описания, должны располагаться достаточно близко друг к другу, чтобы можно было воспринять поверхность без грубых потерь и искажений. Поточечное описание поверхностей применяют в тех случаях, когда поверхность очень сложна, не обладает нужной гладкостью, а детальное представление многочисленных геометрических особенностей важно для практики.
Описание объекта сплошными геометрическими конструктивами (твердотельное моделирование) заключается в представлении сложного объекта в виде объединения простых объемных примитивов. Обычно такие примитивы включают кубы, цилиндры, конусы, эллипсоиды и другие подобные формы. Булевы операции над примитивами позволяют достигать объединения, вычитания и выделения общих частей примитивов. Структуры данных модели этого вида идентичны бинарному дереву, причем узлы (нетерминальные вершины) дерева являются операторами над примитивами, а листья – примитивами.
Следует также отметить метод описания объекта с помощью проволочной сетки (wire-frame), суть которого заключается в представлении поверхности серией пересекающихся линий, принадлежащих поверхности объекта. Как правило, в качестве таких линий принято использовать отрезки прямых. Достоинством проволочного представления является простой и эффективный способ построения объектов.
Для наилучшего восприятия формы объекта необходимо иметь его представление в трехмерном пространстве. Как правило, наглядное представление об объекте можно получить с помощью выполнения операций вращения и переноса, а также путем построения его проекций. Как и двумерном случае, существует три основных преобразования в трехмерном пространстве: перенос (изменение положения), изменение масштаба и вращение.
Преобразование перемещения точки трехмерного пространства P=(x,y,z) в новую точку P'=(x',y',z') можно записать следующим образом: x'=x+Tx, y'=y+Ty, z'=z+Tz, где Tx,Ty,Tz - величины перемещения в направлениях x,y,z соответственно. Определяя точку и операцию переноса как вектор-строку P=(x,y,z), P'=(x',y',z'),T=(Tx,Ty,Tz), преобразование сдвига можно записать в векторной форме: (x',y',z')=(x,y,z)+(Tx,Ty,Tz) или P'=P+T.
Точку трехмерного пространства P=(x,y,z) можно подвергнуть операции масштабирования (растяжения или сжатия) в Sx раз по оси абсцисс, в Sy раз по оси ординат и в Sz раз по оси аппликат. Полученная в результате преобразованная точка P'=(x',y',z') будет выражаться как: x'=x*Sx,y'=y*Sy,z'=z*Sz. Определив S как матрицу
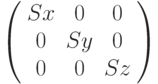
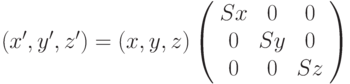
Трехмерные преобразования вращения являются более сложными, чем их двумерные аналоги. В данном случае необходимо дополнительно задать ось вращения. Рассмотрим сначала простейшие случаи, когда ось вращения совпадает с одной из координатных осей.
Найдем матрицу поворота вокруг оси OZ на угол y. Будем записывать матрицу преобразования для левосторонней системы координат. Следует отметить, что в левосторонней системе координат положительными будут повороты, выполняемые по часовой стрелке, если смотреть с конца положительной полуоси в направлении начала координат (рис. 1.9).
В данном случае ось поворота перпендикулярна к плоскости рисунка, и поскольку мы используем левостороннюю систему координат, то вращение вокруг оси OZ сводится к повороту точки на плоскости XOY на угол  . При этом координата z точки вращения не изменяется. Таким образом, формулу поворота точки (x,y,z) вокруг оси OZ на угол
. При этом координата z точки вращения не изменяется. Таким образом, формулу поворота точки (x,y,z) вокруг оси OZ на угол  можно записать следующим образом:
можно записать следующим образом:







