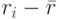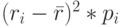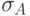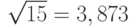|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Доходность и риск
5.5. Количественное измерение риска
Средняя арифметическая ожидаемых доходностей ( 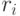 ) инвестиций, взвешенная по вероятности возникновения отдельных значений, называется математическим ожиданием. Условимся называть эту величину средней ожидаемой доходностью:
) инвестиций, взвешенная по вероятности возникновения отдельных значений, называется математическим ожиданием. Условимся называть эту величину средней ожидаемой доходностью:
 |
( 5.5.1) |
где 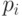 – вероятность получения доходности
– вероятность получения доходности 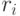 .
.
В статистике количественным измерителем степени разброса значений переменной вокруг ее средней величины (математического ожидания) является показатель дисперсии (  ):
):
 |
( 5.5.2) |
Квадратный корень из дисперсии называется средним квадратическим или стандартным отклонением  :
:
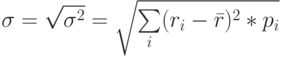 |
( 5.5.3) |
Данный показатель используется в финансовом менеджменте для количественного измерения степени риска планируемых инвестиций. Чем больше разброс ожидаемых значений доходности вложений вокруг их среднеарифметической величины, тем выше риск, сопряженный с данным вложением. Фактическая величина доходности может быть как значительно выше, так и значительно ниже ее средней величины.
Практическая ценность такого подхода заключается не только (и не столько) в применении статистических формул, а в осознании необходимости многовариантного планирования инвестиционных решений. Любые ожидаемые результаты этих решений могут носить лишь вероятностный характер. От финансиста требуется не только правильно применить формулу расчета доходности инвестиций, но и дать количественную оценку вероятности возникновения конкретного результата. Как минимум, необходимо планировать не менее трех вариантов развития событий: оптимистический, пессимистический и наиболее вероятный. Полная вероятность возникновения всех этих вариантов должна быть равна 1.
Например, оценивая две акции А и Б, инвестор пришел к выводу, что распределение вероятностей их ожидаемой доходности можно представить следующим образом:
Среднеарифметическая ожидаемая доходность (математическое ожидание), взвешенная по вероятности каждого варианта составит:
То есть, с точки зрения ожидаемой доходности инвестору безразлично, какую именно акцию приобрести – любая из них должна принести ему 15% дохода. Однако, данная логика рассуждений ошибочна. Прежде всего инвестор должен оценить величину риска, сопряженного с каждым из сравниваемых активов. Для этого ему следует рассчитать стандартные отклонения доходности  по каждой ценной бумаге. Выполним эти расчеты в табл. 5.8:
по каждой ценной бумаге. Выполним эти расчеты в табл. 5.8:
Разброс значений ожидаемой доходности по акции А почти в 20 раз больше, чем по акции Б. Очевидно, что первое вложение является более рискованным, поэтому предлагаемая по нему компенсация риска в виде 15%-ой доходности абсолютно недостаточна. Точно такую же среднюю ожидаемую доходность способна принести менее рискованная акция Б. Схема на рис. 5.2 наглядно иллюстрирует разброс ожидаемых значений доходности по двум акциям: он значительно шире по первому активу (А).На этой схеме изображено распределение вероятностей. В данном случае оно является дискретным, прерывистым, поэтому данные представлены в форме столбцов (гистограмма). В случае непрерывного распределения, график представляет собой плавную кривую.
Тесноту связи двух переменных в статистике измеряют при помощи коэффициентов корреляции, которые рассчитываются по формуле:
 |
( 5.5.4) |
где  – коэффициент ковариации между доходностью акций А и Б.
– коэффициент ковариации между доходностью акций А и Б.
Коэффициент ковариации вычисляется по формуле:
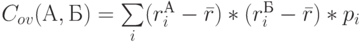 |
( 5.5.5) |
Использовав данные табл. 5.8, получим:
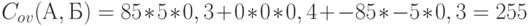
Тогда коэффициент корреляции составит:
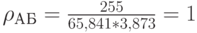
То есть, "поведение" акций на рынке абсолютно идентично, поэтому они не могут быть использованы для диверсификации несистематического риска инвестиционного портфеля. С увеличением стоимости акции А будет возрастать в цене и акция Б, соответственно падение цены на первую акцию обусловливается влиянием тех же факторов, что и на вторую. В случае положительного влияния факторов, инвестор будет богатеть значительно быстрее, однако в противоположном случае, его убытки также будут возрастать опережающими темпами.