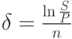|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Временная стоимость денег
2.2 Элементарные финансовые расчеты
В предыдущем параграфе были изложены основные принципы применения процентных вычислений в практических финансовых расчетах. Приведенные в этой лекции примеры относились к банковской деятельности, так как в этой сфере механизм их действия наиболее нагляден и понятен. Однако, сфера использования финансовых вычислений значительно шире, чем расчет параметров банковских кредитов. Хорошее владение основами финансовой математики позволяет сравнивать между собой эффективность отдельных операций и обосновывать наиболее оптимальные управленческие решения. Для анализа финансовых показателей в настоящее время применяются самые изощренные математические методы. Наличие докторской степени по математике пока не является обязательным требованием для финансового менеджера большинства предприятий, однако знание элементарых свойств финансовых показателей и основных взаимосвязей между ними будет ему необходимы начиная с первого дня практической работы.
Большую помощь финансисту оказывают специальные компьютерные программы, а также финансовые калькуляторы, позволяющие автоматизировать вычисление многих показателей. Широкое распространение получило использование финансовых таблиц для начисления сложных процентов и дисконтирования. В этих таблицах приводятся значения множителей наращения (дисконтных множителей) для заданных n и i. Для нахождения наращенной стоимости достаточно умножить известную первоначальную сумму на табличное значение множителя наращения. Аналогично можно найти приведенную величину будущих денег, умножая их сумму на дисконтный множитель из таблицы. Рассмотим некоторые другие элементарные способы использования результатов финансовых вычислений.
В условиях нестабильной экономики банки и другие кредиторы с целью снижения своего процентного риска могут устанавливать переменные ставки процентов для различных финансовых операций. Например, по ссуде в размере 2 млн. рублей общей продолжительностью 120 дней в течение первых двух месяцев будут начисляться 30% годовых, а начиная с 61 дня ежемесячно простая процентная ставка будет увеличиваться на 5% (обыкновенные проценты). Фактически, ссуда разбивается на несколько составляющих, по каждой из которых установлены свои условия. Необходимо найти наращенные суммы по каждой из составляющих, а затем сложить их. Вспомним, что аналогом процентной ставки в статистике является показатель "темп прироста". При начислении простых процентов следует говорить о базисных темпах прироста, т.к. первоначальная сумма  остается неизменной. Данная задача в статистических терминах может быть интерпретирована как сложение базисных темпов
прироста с последующим умножением на первоначальную сумму займа. Общая формула расчета будет иметь следующий вид:
остается неизменной. Данная задача в статистических терминах может быть интерпретирована как сложение базисных темпов
прироста с последующим умножением на первоначальную сумму займа. Общая формула расчета будет иметь следующий вид:
 |
( 1) |
где  общее число периодов, в течение которых проценты начисляются по неизменной ставке. Подставив в это выражение условия нашего примера, получим:
общее число периодов, в течение которых проценты начисляются по неизменной ставке. Подставив в это выражение условия нашего примера, получим:

 |
( 2) |
Подставив условия примера, получим:

Данную задачу можно решить несколько иным путем – рассчитав сначала средние процентные ставки. Расчет средних процентных ставок (или расчет средних доходностей) вообще очень распространенная в финансах операция. Для ее выполнения полезно опять вспомнить о математико-статистической природе процентных ставок. Так как начисление простых процентов происходит в арифметической прогрессии, средняя простая ставка рассчитывается как средняя арифметическая взвешенная.
 |
( 3) |
где  – общее число периодов, в течение которых процентная ставка оставалась неизменной
– общее число периодов, в течение которых процентная ставка оставалась неизменной
Сложные проценты растут в геометрической прогрессии, поэтому средняя сложная процентная ставка рассчитывается как средняя геометрическая взвешенная. В качестве весов в обоих случаях используются продолжительности периодов, для которых действовала фиксированная ставка.
![$\bar i_с_л=\sqrt[N]{\prod_{j=1}^N} (1+i_j)^n^1-1$,](/sites/default/files/tex_cache/a11d0a71c378879d50bc329479f15ab2.png) |
( 4) |
Снова используем данные нашего примера. В случае начисления простых процентов получим:


То есть средняя процентная ставка составила 33,75% и начисление процентов по этой ставке за весь срок ссуды дает такой же результат, как и тот, что был получен по формуле (1). Для сложных процентов выражение примет вид:


Начисление процентов по средней процентной ставке 33,69% также дает результат, эквивалентный тому, что был получен по формуле (2).
Понимание различий механизмов наращения простых и сложных процентов помогает избегать довольно распространенных ошибок. Например, следует помнить, что такой процесс как инфляция развивается в геометрической, а не в арифметической прогресссии, то есть к нему должны применяться правила начисления сложных, а не простых процентов. Темпы прироста цен в этом случае являются цепными, а не базисными, т.к. в каждом последующем месяце рост цен относится к предыдущему месяцу, а не к началу года или какой-либо иной неизменной базе. Например, если инфляция в январе составила 5%, в феврале 4%, а в марте 9%, то общая инфляция за квартал будет равна не 18% (сумма месячных показателей), а 19,03% (1,05 * 1,04 * 1,09 – 1). Среднемесячный уровень инфляции за этот квартал составит (1,05 * 1,04 * 1,09)1/3 - 1 = 5,98%. С другой стороны, если объявляется, что среднемесячная инфляция за год составила 5,98%, то это не значит, что общая инфляция за год в 12 раз больше (71,76%). На самом деле годовая инфляция в этом случае составит свыше 100,7% (1,059812 - 1).
В предыдущей лекции обращалось внимание на сложности, возникающие при попытке понять смысл антисипативного начисления процентов. Рассмотрим ситуацию, в которой необходимо прибегнуть именно к этому способу. Например, коммерсант предлагает вместо оплаты наличными выписать на стоимость закупленных материалов вексель в сумме 500 тыс. рублей со сроком оплаты через 90 дней, который может быть учтен в банке по простой учетной ставке 25% годовых ( коммерческие проценты с точным числом дней ссуды). Для определения суммы, которую понадобится проставить в этом векселе ему необходимо начислить проценты на стоимость товаров, используя антисипативный метод. Сумма векселя составит 533,333 тыс. рублей (500 * 1 / (1 – 90 / 360 * 0,25). Если продавец в этот же день учтет этот вексель в банке (на оговоренных условиях), то получит на руки ровно 500 тыс. рублей (533,333 * (1 – 90 / 360 * 0,25)). Таким образом, начисление антисипативных процентов используется для определения наращенной суммы, которая затем будет дисконтироваться по той же самой ставке, по которой производилось начисление. Такое чисто техническое использование наращения по учетной ставке является преобладающим в практических расчетах.
Наряду с расчетом будущей и современной величины денежных средств часто возникают задачи определения других параметров финансовых операций: их продолжительности и величины процентной или учетной ставок. Например, может возникнуть вопрос: сколько времени понадобится, чтобы данная сумма при заданном уровне процентной ставки удвоилась, или при каком уровне учетной ставки в течение года исходная сумма возрастет в полтора раза? Решение подобных задач сводится к преобразованию соответствующей формулы наращения ( дисконтирования ) таким образом, чтобы вычислить значение неизвестного параметра. Например, если надо рассчитать продолжительность ссуды по известным первоначальной и будущей суммам, а также уровню простой процентной ставки, то преобразуя формулу начисления простых декурсивных процентов (S = P * (1 + ni)), получим формулу (5) из табл. 2.1 (Все формулы и их ну мерация приведены в табл. 2.1). По такой же формуле будет определяться срок до погашения обязательства при математическом дисконтировании.
Определение срока финансовой операции для антисипативного начисления процентов и банковского учета производится по формуле (6) из табл. 2.1 Например, нужно определить через какой период времени произойдет удвоение суммы долга при начислении на нее 20% годовых простых а) при декурсивном методе начисления процентов; б) при использовании антисипативного метода. Временная база в обоих случаях принимается равной 365 дней ( точные проценты ). Применив формулы (5) и (6), получим:


Эти же формулы можно применить для определения срока до погашения обязательств при дисконтировании. Например, по векселю номиналом 700 тыс. рублей банк выплатил 520 тыс. рублей, произведя его учет по простой ставке 32% годовых. Чему равен срок до погашения векселя? Применив формулу (6), получим:

Товар, стоимостью 1,5 млн. рублей оплачивается на условиях коммерческого кредита, предоставленного под 15% годовых (простая процентная ставка, временная база 360 дней). Сумма оплаты по истечении срока кредита составила 1 млн. 650 тыс. рублей. Чему равен срок предоставленного кредита? Из формулы (5) следует:

Например, сколько лет должен пролежать на банковском депозите под 20% (сложная процентная ставка  ) вклад 100 тыс. рублей, чтобы его сумма составила 250 тыс. рублей? Подставив данные в формулу (7), получим:
) вклад 100 тыс. рублей, чтобы его сумма составила 250 тыс. рублей? Подставив данные в формулу (7), получим:

Если начисление процентов при этих же условиях будет производиться ежемесячно, то в соответствии с формулой (8):

Чтобы избежать использования вычислений логарифмов, разработаны упрощенные способы приближенных вычислений срока финансовых операций. Один из них - "правило 70" - позволяет определить период удвоения первоначальной суммы при начислении сложных процентов по приближенной формуле 70% / i. Проверим его на нашем примере, заменив значение наращенной суммы 250 тыс. рублей на 200 тыс. рублей. По "правилу 70" эта сумма должна быть накоплена через 3,5 года (0,7 / 0,2). Подставив соответствующие значения в формулу (7) получим 3,8 года.

 – длительность в днях,
– длительность в днях,  – временная база)
– временная база)


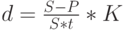
 – длительность, лет)
– длительность, лет)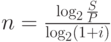

 (
( 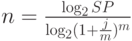

 (
( 

 (
(