Три алгоритма на графах

Задачи

Задача 11.1. Цикл в связном неориентированном графе называется Эйлеровым, если он проходит по одному разу через каждое ребро графа. Докажите, что в таком графе имеется Эйлеров цикл тогда и только тогда, когда степени всех его вершин четны (такие графы называются четными.

Указание. Достаточность можно установить, доказав правильность следующей процедуры построения Эйлерова цикла.

1. Выбрать произвольную вершину a и построить цикл, начинающийся и закачивающийся в a, следуя правилу (*): прийдя в некоторую вершину, выйти из нее по произвольному ребру, еще не включенному в цикл.
2. Если построенный цикл содержит не все ребра, то выбрать среди вершин, через которые он проходит, произвольную вершину b, инцидентную еще не пройденному ребру (почему такая вершина найдется?), и построить, начиная с нее, цикл, следуя тому же правилу (*). Объединить этот цикл с построенным ранее.
3. Повторять пункт (2) до тех пор, пока построенный цикл не станет Эйлеровым.

Задача 11.2. Используя результаты предыдущей задачи, определить по неориентированному графу G=(V,E) четный ли он. Если он не является четным, то удалить из него минимальное число ребер, чтобы он стал четным. Построить в исходном или в получившемся после удаления ребер четном графе Эйлеров цикл.

V={a,b,c,e,f,g,h, k,m,n }, E={ (a,c), (a,h), (a,m),(a,k), (b,c),(b,k), (b,f), (b,m), (c,k), (c,m), (e,f), (e,g), (f,k), (f,n),(g,m), (g,h), (h,k), (h,m),(k,n) }.

Задача 11.3. Неориентированный граф G=(V,E) называется двудольным, если его вершины можно разбить на две непересекающихся части X и Y ( ) так, что каждое ребро из 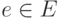соединяет вершину из X с вершиной из Y. Такой граф также называется бихроматическим, так как его вершины можно раскрасить в два цвета так, что соседние вершины будут окрашены в разные цвета.

Докажите, что граф является двудольным тогда и только тогда, когда в нем нет циклов нечетной длины.

Указание. Достаточность можно установить, доказав правильность следующей процедуры разбиения V на X и Y:

1. Поместить произвольную вершину 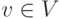в X и отметить ее знаком +.

2. ПОКА имеются неотмеченные вершины с отмеченными соседями

   ВЫПОЛНЯТЬ {

   • Поместить все неотмеченные вершины с соседями из X в Y и отметить их знаком - ;

   • Поместить все неотмеченные вершины с соседями из Y в X и отметить их знаком +

     };

3. ЕСЛИ после завершения цикла 2 в V остались неотмеченные вершины

   ТО поместить произвольную такую вершину v в X, отметить ее знаком + и снова повторить цикл 2

   ИНАЧЕ выдать в качестве результата полученные множества: X - вершины, отмеченные +, и Y - вершины, отмеченные -.

Для доказательства корректности этой процедуры установите, что в процессе разметки ни одна вершина не получит соседа с той же меткой.

Задача 11.4. Используя результаты предыдущей задачи, определить, является ли заданный ниже неориентированный граф G=(V,E) двудольным. Если он не двудольный, то каково минимальное число ребер, которые нужно из него удалить, чтобы он стал двудольным? Приведите обоснование ответа.

V={a,b,c,e,f,g,h, k,m,n }, E={ (a,h), (a,n),(a,k), (b,k), (b,f), (b,m), (c,k), (c,h), (e,f), (e,g), (f,a), (f,m),(g,m), (m,n) }.

Задача 11.5. Найти минимальное остовное дерево для неориентированного графа G=(V,E), где V={v₁,v₂,v₃,v₄,v₅,v₆,v₇,v₈,v₉}, E = {(v₁,v₂,18), (v₁,v₃,2), (v₃,v₂,4), (v₃,v₄,6), (v₃,v₅,8), (v₄,v₆,5), (v₅,v₄,4), (v₆,v₁,7), (v₆,v₈,4), (v₆,v₇,3), (v₇,v₅,1), (v₇,v₈,7), (v₈,v₁,5), (v₈,v₉,3), (v₉,v₁,1)} (третий параметр в скобках - стоимость ребра).

Задача 11.6. Пусть S= (V,T) - остовное дерево наименьшей стоимости, построенное алгоритмом МИНОД для нагруженного неориентированного графа G=(V,E) с n вершинами. Пусть c₁ <= c₂ <= ... <= c_n-1 - это последовательность длин ребер из T, упорядоченных по возрастанию. Пусть S' - произвольное остовное дерево для G с длинами ребер d₁ <= d₂ <= ... <= d_n-1. Показать, что c_i <= d_i для всех i: 1 <= i <= n-1.

Задача 11.7. Пусть e - ребро максимального веса в некотором цикле графа G=(V,E). Докажите, что существует минимальный остов графа G'=(V,E \ {e}), который является также минимальным остовом графа G.

Задача 11.8. Пусть D=(V,T) - это глубинный остов, построенный алгоритмом обхода "в глубину" для графа G=(V, E). Докажите, что для каждого обратного ребра 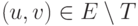либо u является предком v в D, либо v является предком u в D.

Задача 11.9. Модифицируйте алгоритм поиска в глубину так, чтобы он вычислял функцию ВЕРХ(v) и распечатывал список всех мостов графа.

Задача 11.10. Обойти (занумеровать) вершины заданного неориентированного графа G с помощью алгоритма обхода "в глубину" и построить дерево этого обхода.

G = (V,E), где V = {v₁,v₂,v₃,v₄,v₆,v₇, v₈,v₉,v₁₀,v₁₁},

E ={(v₁,v₂),(v₁,v₄),(v₁,v₈),(v₇,v₈), (v₂,v₉),(v₉,v₁₁), (v₃,v₈),(v₆,v₃), (v₃,v₇),(v₆,v₇), (v₁₀,v₉), (v₁₀,v₁₁) }.

Какое обратное ребро 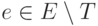и цикл в G обнаружились в этом обходе первыми? Вычислите для каждой вершины v значение ВЕРХ(v) и определите все мосты графа G.

Задача 11.11. Измените алгоритм обхода "в глубину" так, чтобы он позволил перечислить все связные компоненты неориентированного графа.

Задача 11.12. Определить для заданного нагруженного графа G=(V, E) и выделенной вершины 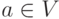длины кратчайших путей из этой вершины в остальные вершины G и построить дерево этих путей.

V={a, b, c, d, e,f }, E= {(a,b; 154), (a,c; 17),(a,d; 214), (a,e; 63), (b, d; 25), (c,e; 33), (c, d; 192), ( c,b; 123), (d, f; 5), (e,f; 140), (d,e; 10)}, (здесь каждая скобка (u,v; D) задает ребро и его "вес" c(u,v)=D ).

Задача 11.13. Где в доказательстве правильности алгоритма Дейкстры используется неотрицательность весов ребер? Приведите пример графа (с отрицательными весами), для которого алгоритм Дейкстры дает неверный ответ.

Задача 11.14. Докажите, что на каждом шаге алгоритма Дейкстры кратчайший путь из исходной вершины в любую вершину множества S проходит только через вершины множества S.

Задача 11.15. Сколько раз может меняться для одной вершины v значение D[v] в ходе работы алгоритма Дейкстры для графа с 6 вершинами? Привести пример на каждый возможный случай.