Методы сжатия изображений
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 10.10.2007 | Доступ: свободный | Студентов: 1478 / 158 | Оценка: 4.36 / 4.18 | Длительность: 14:22:00
Темы: Компьютерная графика, Алгоритмы и дискретные структуры
Специальности: Программист
Теги: I-MPEG, JPEG, mpeg, ppm, RLE, u-кадры, алгоритмы, алфавит, архивация, видео, графика, декодирование, кодер, моделирование, нормализация, поиск, потоки, приложения, сжатие, стандарты, форматы, цвета, элементы
Лекция 6:

Проблемы алгоритмов архивации с потерями
A
|
версия для печати
< Лекция 5 || Лекция 6: 12345 || Лекция 7 >

Фрактальный алгоритм

Идея метода

Фрактальная архивация основана на том, что мы представляем изображение в более компактной форме - с помощью коэффициентов системы итерируемых функций ( Iterated Function System - далее по тексту как IFS ). Прежде, чем рассматривать сам процесс архивации, разберем, как IFS строит изображение, т.е. процесс декомпрессии.

Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х_координата, у_координата, яркость).

Наиболее наглядно этот процесс продемонстрировал Барнсли в своей книге " Fractal Image Compression ". Там введено понятие Фотокопировальной Машины, состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран: (рис. 6.3)

  • Линзы могут проецировать часть изображения произвольной формы в любое другое место нового изображения.
  • Области, в которые проецируются изображения, не пересекаются.
  • Линза может менять яркость и уменьшать контрастность.
  • Линза может зеркально отражать и поворачивать свой фрагмент изображения.
  • Линза должна масштабировать (причем только уменьшая) свой фрагмент изображения.
Машина Барнсли

Рис. 6.3. Машина Барнсли

Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы Машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется "неподвижной точкой" или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.

Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого - самоподобный математический объект).

Наиболее известны два изображения, полученных с помощью IFS: "треугольник Серпинского" (рис. 6.4) и "папоротник Барнсли" рис. 6.5.

Треугольник Серпинского. Задается 3 преобразованиями

Рис. 6.4. Треугольник Серпинского. Задается 3 преобразованиями

"Треугольник Серпинского" задается тремя, а "папоротник Барнсли" четырьмя аффинными преобразованиями (или, в нашей терминологии, "линзами"). Каждое преобразование кодируется буквально считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.

Папоротник Барнсли. Задается 4 преобразованиями

Рис. 6.5. Папоротник Барнсли. Задается 4 преобразованиями
Упражнение: Укажите в изображении 4 области, объединение которых покрывало бы все изображение, и каждая из которых была бы подобна всему изображению (не забывайте о стебле папоротника).

Из вышесказанного становится понятно, как работает архиватор, и почему ему требуется так много времени. Фактически, фрактальная компрессия - это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований (рис. 6.6).


Рис. 6.6.

В худшем случае, если не будет применяться оптимизирующий алгоритм, потребуется перебор и сравнение всех возможных фрагментов изображения разного размера. Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов. Причем, даже резкое сужение классов преобразований, например, за счет масштабирования только в определенное количество раз, не дает заметного выигрыша во времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения.

Далее приводятся основные определения и теоремы, на которых базируется фрактальная компрессия. Этот материал более детально и с доказательствами рассматривается в [6.3] и в [6.4].

Определение. Преобразование w:R^2 \to R^2, представимое в виде

w(\bar \rangle ) = w \left( \begin{array}{c} x \\ y \\ \end{array} \right) = \left( \begin{array}{cc} a & b \\ c & b \\ \end{array} \right) \left( \begin{array}{c} x \\ y \\ \end{array} \right) + \left( \begin{array}{c} e \\ f \\ \end{array} \right)

где a, b, c, d, e, f действительные числа и \left( {\matrix{ x & y \cr } } \right) \in R^2 называется двумерным аффинным преобразованием.

Определение. Преобразование , представимое в виде

w(\bar \rangle ) = w \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) = \left( \begin{array}{ccc} a & b & t\\ c & d & u\\ r & s & p\\ \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) + \left( \begin{array}{c} e \\ f \\ q \\ \end{array} \right)

где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и \left( {\matrix{ x & y & z \cr } } \right) \in R^3 называется трехмерным аффинным преобразованием.

Определение. Пусть f:{\rm X} \to {\rm X} - преобразование в пространстве Х. Точка x_f \in {\rm X} такая, что f(x_f ) = x_f называется неподвижной точкой (аттрактором) преобразования.

Определение. Преобразование 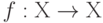f:{\rm X} \to {\rm X} в метрическом пространстве (Х, d) называется сжимающим, если существует число s: 0 \le s < 1 , такое, что

d(f(x),f(y)) \le s \cdot d(x,y)\matrix{ {} & {\forall \matrix{ {x,y \in {\rm X}} & {} \cr } } \cr }

Замечание: Формально мы можем использовать любое сжимающее отображение при фрактальной компрессии, но реально используются лишь трехмерные аффинные преобразования с достаточно сильными ограничениями на коэффициенты.

Теорема. (О сжимающем преобразовании)

Пусть f:{\rm X} \to {\rm X} - сжимающее преобразование в полном метрическом пространстве (Х, d). Тогда существует в точности одна неподвижная точка x_f \in {\rm X} этого преобразования, и для любой точки x \in {\rm X} последовательность \left\{ {\left. {f^n (x)\matrix{ : & {n = } \cr } \matrix{ {0,1,2...} & {} \cr } } \right\}} \right. сходится к x_f .

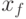Более общая формулировка этой теоремы гарантирует нам сходимость.

Определение. Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или S(x,y) \in \left[ {0...1} \right]\matrix{ {} & {\forall x,y} \cr } \in \left[ {0...1} \right]

Пусть трехмерное аффинное преобразование w_i :R^3 \to R^3, записано в виде

w_i(\bar \rangle ) = w_i \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) = \left( \begin{array}{ccc} a & b & 0\\ c & d & 0\\ 0 & 0 & p\\ \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) + \left( \begin{array}{c} e \\ f \\ q \\ \end{array} \right)

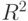и определено на компактном подмножестве D_i декартова квадрата [0..1]x[0..1] (мы пользуемся особым видом матрицы преобразования, чтобы уменьшить размерность области определения с R^3 до R^2 ). Тогда оно переведет часть поверхности S в область R_i, расположенную со сдвигом (e,f) и поворотом, заданным матрицей

\left( \begin{array}{ccc} a & b & 0\\ c & d & 0\\ 0 & 0 & 0\\ \end{array} \right) .

При этом, если интерпретировать значения функции S(x,y) \in \left[ {0...1} \right] как яркость соответствующих точек, она уменьшится в p раз (преобразование обязано быть сжимающим) и изменится на сдвиг q.

Определение. Конечная совокупность W сжимающих трехмерных аффинных преобразований 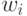w_i, определенных на областях D_i, таких, что w_i (D_i ) = R_i и R_i \cap R_j = \matrix{ {\not o} & {\forall i \ne j} \cr } , называется системой итерируемых функций (IFS).

Системе итерируемых функций однозначно сопоставляется неподвижная точка - изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии - в проведении итераций системы до стабилизации полученного изображения (неподвижной точки IFS). На практике бывает достаточно 7-16 итераций. Области R_i в дальнейшем будут именоваться ранговыми, а области D_i - доменными.

Дальше >>
< Лекция 5 || Лекция 6: 12345 || Лекция 7 >

Вопросы и ответы

вопросов: 0