Методы сжатия без потерь
Арифметическое сжатие
Классический вариант алгоритма
Сжатие по методу Хаффмана постепенно вытесняется арифметическим сжатием.
Свою роль в этом сыграло то, что закончились сроки действия патентов, ограничивающих
использование арифметического сжатия. Кроме того, алгоритм Хаффмана приближает
относительные частоты появления символов в потоке частотами кратными степени двойки
(например, для символов  ,
,  ,
,  ,
, 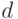 с вероятностями 1/2, 1/4, 1/8, 1/8 будут использованы коды 0, 10, 110, 111),
а арифметическое сжатие дает лучшую степень приближения частоты. По теореме Шеннона,
наилучшее сжатие в двоичной арифметике мы получим, если будем кодировать символ с
относительной частотой
с вероятностями 1/2, 1/4, 1/8, 1/8 будут использованы коды 0, 10, 110, 111),
а арифметическое сжатие дает лучшую степень приближения частоты. По теореме Шеннона,
наилучшее сжатие в двоичной арифметике мы получим, если будем кодировать символ с
относительной частотой  с помощью
с помощью  битов.
битов.
На графике, показанном на рис 1.2 приводится сравнение оптимального кодирования и кодирования
по методу Хаффмана. Хорошо видно, что в ситуации, когда относительные частоты не являются
степенями двойки, сжатие становится менее эффективным (мы тратим больше битов, чем это
необходимо). Например, если у нас два символа  и
и  с вероятностями
253/256 и 3/256, то в идеале мы должны потратить на цепочку из 256 байт
с вероятностями
253/256 и 3/256, то в идеале мы должны потратить на цепочку из 256 байт 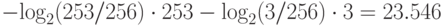 ,
т.е. 24 бита. При кодировании по Хаффману мы закодируем
,
т.е. 24 бита. При кодировании по Хаффману мы закодируем  и
и  как 0 и 1, и нам придется потратить 1·253+1·3= 256 битов, т.е. в 10 раз больше.
Рассмотрим алгоритм, дающий результат, близкий к оптимальному.
как 0 и 1, и нам придется потратить 1·253+1·3= 256 битов, т.е. в 10 раз больше.
Рассмотрим алгоритм, дающий результат, близкий к оптимальному.
Арифметическое сжатие - достаточно изящный метод, в основе которого лежит очень простая идея. Мы представляем кодируемый текст в виде дроби, при этом строим дробь таким образом, чтобы наш текст был представлен как можно компактнее. Для примера рассмотрим построение такой дроби на интервале [0, 1) (0 - включается, 1 - нет). [0, 1) выбран потому, что он удобен для объяснений. Мы разбиваем его на подинтервалы с длинами, равными вероятностям появления символов в потоке. В дальнейшем будем называть их диапазонами соответствующих символов.
Пусть мы сжимаем текст "КОВ.КОРОВА" (что, очевидно, означает "коварная корова"). Распишем вероятности появления каждого символа в тексте (в порядке убывания) и соответствующие этим символам диапазоны (см. табл 1.1):
| Символ | Частота | Вероятность | Диапазон |
|---|---|---|---|
| О | 3 | 0.3 | [0.0; 0.3) |
| К | 2 | 0.2 | [0.3; 0.5) |
| В | 2 | 0.2 | [0.5; 0.7) |
| Р | 1 | 0.1 | [0.7; 0.8) |
| А | 1 | 0.1 | [0.8; 0.9) |
| "" | 1 | 0.1 | [0.9; 1.0) |
Будем считать, что эта таблица известна в компрессоре и декомпрессоре. Кодирование заключается в уменьшении рабочего интервала. Для первого символа в качестве рабочего интервала берется [0, 1). Мы разбиваем его на диапазоны в соответствии с заданными частотами символов (см. таблицу диапазонов). В качестве следующего рабочего интервала берется диапазон, соответствующий текущему кодируемому символу. Его длина пропорциональна вероятности появления этого символа в потоке. Далее считываем следующий символ. В качестве исходного берем рабочий интервал, полученный на предыдущем шаге, и опять разбиваем его в соответствии с таблицей диапазонов. Длина рабочего интервала уменьшается пропорционально вероятности текущего символа, а точка начала сдвигается вправо пропорционально началу диапазона для этого символа. Новый построенный диапазон берется в качестве рабочего, и т.д.
Используя исходную таблицу диапазонов, кодируем текст "КОВ.КОРОВА":
Исходный рабочий интервал [0, 1).
Символ "К" [0.3; 0.5) получаем [0.3000; 0.5000).
Символ "О" [0.0; 0.3) получаем [0.3000; 0.3600).
Символ "В" [0.5; 0.7) получаем [0.3300; 0.3420).
Символ "." [0.9; 1.0) получаем [0,3408; 0.3420).
Графически процесс кодирования первых трех символов представлен на рис 1.3
Таким образом, окончательная длина интервала равна произведению вероятностей всех
встретившихся символов, а его начало зависит от порядка следования символов в потоке.
Если обозначить диапазон символа c как ![[a[c],b[c])](/sites/default/files/tex_cache/8ef2375e4c8ab15a81f04e4fd088e4f4.png) , а интервал
для
, а интервал
для  -го кодируемого символа потока как
-го кодируемого символа потока как  , то алгоритм
сжатия может быть записан как:
, то алгоритм
сжатия может быть записан как:
l0=0; h0=1; i=0;
while(not DataFile.EOF()){
c = DataFile.ReadSymbol(); i++;
li = li-1 + a[c]*(hi-1 - li-1);
hi = hi-1 + b[c]*(hi-1 - li-1);
};Большой вертикальной чертой на рисунке выше обозначено произвольное число,
лежащее в полученном при работе интервале  . Для последовательности
"КОВ.", состоящей из 4 символов, за такое число можно взять 0.341. Этого числа
достаточно для восстановления исходной цепочки, если известна исходная таблица диапазонов
и длина цепочки.
. Для последовательности
"КОВ.", состоящей из 4 символов, за такое число можно взять 0.341. Этого числа
достаточно для восстановления исходной цепочки, если известна исходная таблица диапазонов
и длина цепочки.
Рассмотрим работу алгоритма восстановления цепочки. Каждый следующий интервал вложен
в предыдущий. Это означает, что если есть число 0.341, то первым символом в цепочке может
быть только "К", поскольку только его диапазон включает это число. В качестве
интервала берется диапазон "К" - [0.3; 0.5) и в нем находится
диапазон ![[a[c],b[c])](/sites/default/files/tex_cache/8ef2375e4c8ab15a81f04e4fd088e4f4.png) , включающий 0.341. Перебором всех возможных символов по
приведенной выше таблице находим, что только интервал [0.3; 0.36), соответствующий
диапазону для "О" включает число 0.341. Этот интервал выбирается в качестве
следующего рабочего и т.д. Алгоритм декомпрессии можно записать так:
, включающий 0.341. Перебором всех возможных символов по
приведенной выше таблице находим, что только интервал [0.3; 0.36), соответствующий
диапазону для "О" включает число 0.341. Этот интервал выбирается в качестве
следующего рабочего и т.д. Алгоритм декомпрессии можно записать так:
l0=0; h0=1; value=File.Code();
for(i=1; i<=File.DataLength(); i++){
for(для всех cj){
li = li-1 + a[cj]*(hi-1 - li-1);
hi = hi-1 + b[cj]*(hi-1 - li-1);
if ((li <= value) && (value < hi)) break;
};
DataFile.WriteSymbol(cj);
};Где value - прочитанное из потока число (дробь), а c -
записываемые в выходной поток распаковываемые символы. При использовании алфавита из 256
символов  , внутренний цикл выполняется достаточно долго, однако его можно
ускорить. Заметим, что поскольку
, внутренний цикл выполняется достаточно долго, однако его можно
ускорить. Заметим, что поскольку ![b[c_{j + 1} ] = a[c_j ]](/sites/default/files/tex_cache/66c558941637e18334a4933c13d93395.png) (см. приведенную выше
таблицу диапазонов), то
(см. приведенную выше
таблицу диапазонов), то  для
для 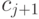 равно
равно  для
для  , а последовательность
, а последовательность  для
для  строго возрастает с ростом j. Т.е. количество операций во внутреннем цикле
можно сократить вдвое, поскольку достаточно проверять только одну границу интервала.
Также, если у нас мало символов, то, отсортировав их в порядке уменьшения вероятностей,
мы сокращаем число итераций цикла и, таким образом, ускоряем работу декомпрессора. Первыми
будут проверяться символы с наибольшей вероятностью, например в нашем примере мы с
вероятностью
строго возрастает с ростом j. Т.е. количество операций во внутреннем цикле
можно сократить вдвое, поскольку достаточно проверять только одну границу интервала.
Также, если у нас мало символов, то, отсортировав их в порядке уменьшения вероятностей,
мы сокращаем число итераций цикла и, таким образом, ускоряем работу декомпрессора. Первыми
будут проверяться символы с наибольшей вероятностью, например в нашем примере мы с
вероятностью  будем выходить из цикла уже на втором символе из шести.
Если число символов велико, существуют другие эффективные методы ускорения поиска символов
(например, бинарный поиск).
будем выходить из цикла уже на втором символе из шести.
Если число символов велико, существуют другие эффективные методы ускорения поиска символов
(например, бинарный поиск).
Хотя приведенный выше алгоритм вполне работоспособен, он будет работать медленно,
по сравнению с алгоритмом, оперирующим двоичными дробями. Двоичная дробь задается как 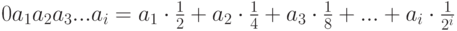 .
Таким образом, при сжатии нам необходимо дописывать в дробь дополнительные знаки до тех пор,
пока получившееся число не попадет в интервал, соответствующий закодированной цепочке.
Получившееся число полностью задает закодированную цепочку при аналогичном алгоритме
декодирования. Графически схема работы алгоритма показана на рис 1.4
.
Таким образом, при сжатии нам необходимо дописывать в дробь дополнительные знаки до тех пор,
пока получившееся число не попадет в интервал, соответствующий закодированной цепочке.
Получившееся число полностью задает закодированную цепочку при аналогичном алгоритме
декодирования. Графически схема работы алгоритма показана на рис 1.4
 ), используя
приведенную выше таблицу диапазонов, если известно, что длина текста 10 символов.
), используя
приведенную выше таблицу диапазонов, если известно, что длина текста 10 символов.Интересной особенностью арифметического кодирования является способность сильно сжимать отдельные длинные цепочки. Например, один бит "1" (двоичное число "0.1") для нашей таблицы интервалов однозначно задает цепочку "ВОООООООООО…" произвольной длины (например, 1000000000 символов). Т.е. если наш файл заканчивается одинаковыми символами, например массивом нулей, то этот файл может быть сжат с весьма впечатляющей степенью сжатия. Очевидно, что длину исходного файла при этом следует передавать декомпрессору явным образом перед сжатыми данными, как это делалось в приведенных выше примерах.
Приведенный выше алгоритм может сжимать только достаточно короткие цепочки из-за
ограничений разрядности всех переменных. Чтобы избежать этих ограничений, реальный
алгоритм работает с целыми числами и оперирует с дробями, числитель и знаменатель
которых являются целыми числами (например, знаменатель равен 10000h = 65536). При этом
с потерей точности можно бороться, отслеживая сближение  и
и  и умножая числитель и знаменатель представляющей их дроби на какое-то число (удобно на 2).
С переполнением сверху можно бороться, записывая старшие биты в
и умножая числитель и знаменатель представляющей их дроби на какое-то число (удобно на 2).
С переполнением сверху можно бороться, записывая старшие биты в  и
и  в файл, тогда, когда они перестают меняться (т.е. реально уже не
участвуют в дальнейшем уточнении интервала). Перепишем таблицу диапазонов с учетом
сказанного выше. Полученные данные занесём в табл. 1.2
в файл, тогда, когда они перестают меняться (т.е. реально уже не
участвуют в дальнейшем уточнении интервала). Перепишем таблицу диапазонов с учетом
сказанного выше. Полученные данные занесём в табл. 1.2



