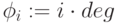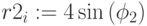Графика
3.2.2. Графики в полярных координатах
В MathCAD полярные графики рисуются с использованием стандартных преобразований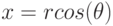 
и 
. Предполагается, что r и 
могут принимать и положительные, и отрицательные значения. Типичный полярный график показывает зависимость выражения для радиуса от угла.
Построение графика
Полярный график строится с использованием шаблона полярного графика на панели Графика. Выражение для функции и угла вводятся в соответствующие шаблоны графика. Можно построить несколько графиков на одном и том же чертеже. Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).
- Определить
как функцию , - заполнить шаблоны,
- отобразить график в полярных координатах (Рис.3.13).
Форматирование графика
Используется команда меню Format/Graph/Plar Plot (Формат/Графика/Полярный график) или двойной щелчок на графике. Окно форматирования такое же, как и для декартовых графиков.
Установка границ на осях координат
По умолчанию устанавливаются верхние и нижние границы на радиальной оси. Для линейного масштаба верхняя граница — максимальное значение радиуса, нижняя граница — ноль. Чтобы вручную установить максимальное значение на радиальной оси, щёлкнуть на числе в верхнем поле ввода и впечатать новое число.
Так же, как и для декартовых графиков, можно использовать индексную переменную, отобразить в полярных координатах один вектор значений относительно другого.
Пример 3.6
Построить график функций 
, 
в полярных координатах с разным шагом по углу, разной сеткой (Рис.3.14, Рис.3.15).
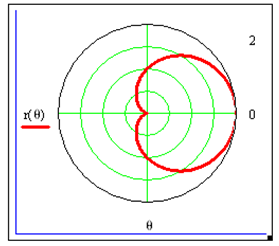
- задан автомасштаб, автосетка. Пределы изменения радиуса от 0 до 4 .
- задан угол в радианах с шагом ?/5. Заданы пределы угла
Пределы изменения радиуса от 0 до 4 . - функция задана как индексная переменная. Угол задан в градусах, от 0 до 90. Пределы изменения радиуса от 1 до 2 . Введена сетка 2х8.
a) 
b)
c) 
