НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 12: Дополнительные свойства контекстно-свободных языков

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 2517 / 1036 | Оценка: 4.56 / 4.26 | Длительность: 20:40:00

ISBN: 978-5-9556-0062-8

Темы: Программирование, Алгоритмы и дискретные структуры, Математика

Специальности: Математик

Теги: beta, finite, grammar, xml, автоматы, анализ, булева формула, дерево вывода, контекстно-свободная грамматика, контекстно-свободный язык, метка перехода, моноид, нетерминальный символ, протоколы, регулярные выражения, теория, шаг индукции, элементы

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

11.2. Гомоморфизмы и контекстно-свободные языки

Теорема 11.2.1. Для любого гомоморфизма $h \colon \Sigma_1^* \farrow \Sigma_2^*$ и контекстно-свободного языка $L \subseteq \Sigma_1^*$ язык h(L) является контекстно-свободным.

Доказательство. Приведем здесь доказательство, использующее МП-автоматы, хотя эту теорему легко доказать и с помощью контекстно-свободных грамматик. Пусть язык L распознается МП-автоматом 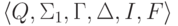$\lalg Q , \Sigma_1 , \Gamma , \Delta , I , F \ralg$ . Тогда язык h(L) распознается МП-автоматом $\lalg Q , \Sigma_2 , \Gamma , \Delta' , I , F \ralg$ , где

$\Delta' = \{ \lp \lp p , h ( x ) , \beta \rp , \lp q , \gamma \rp \rp \mid \lp \lp p , x , \beta \rp , \lp q , \gamma \rp \rp \in \Delta \} .$

Пример 11.2.2. Пусть $\Sigma_1 = \{ a , b , c \}$ и $\Sigma_2 = \{ a , b \}$ . Рассмотрим контекстно-свободный язык L, порождаемый грамматикой

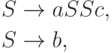
$\begin{align*} S \; & {\to} \; aSSc , \\ S \; & {\to} \; b , \end{align*}$

и гомоморфизм $h \colon \Sigma_1^* \farrow \Sigma_2^*$ , заданный равенствами h(a) = a, h(b) = bba и h(c) = a. Тогда язык h(L) порождается контекстно-свободной грамматикой

$\begin{align*} S \; & {\to} \; aSSa , \\ S \; & {\to} \; bba , \end{align*}$

Упражнение 11.2.3. Пусть гомоморфизм $h \colon \{a,b,c\}^* \farrow \{a,b\}^*$ задан соотношениями h(a) = b, $h(b) = \varepsilon$ , h(c) = a. Рассмотрим язык L, порождаемый грамматикой

$\begin{align*} S \; & {\to} \; a , \\ S \; & {\to} \; b S , \\ S \; & {\to} \; c S S . \end{align*}$

Найти контекстно-свободную грамматику для языка h(L).

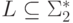Теорема 11.2.4. Для любого гомоморфизма $h \colon \Sigma_1^* \farrow \Sigma_2^*$ и контекстно-свободного языка $L \subseteq \Sigma_2^*$ язык h^-1(L) является контекстно-свободным.

Доказательство. Введем обозначение

$\cala = \{ x \in \Sigma_2 ^* \mid x \suffix h ( a ) \mathspace\text{для некоторого}\mathspace a \in \Sigma_1 \} .$

Пусть язык L распознается МП-автоматом $\lalg Q , \Sigma_2 , \Gamma , \Delta , I , F \ralg$ . Без ограничения общности можно считать, что для каждого перехода $\lp \lp p , x , \beta \rp , \lp q , \gamma \rp \rp \in \Delta$ выполняется неравенство $| x | \leq 1$ . Можно проверить, что в этом случае язык h^-1(L) распознается МП-автоматом $\lalg Q' , \Sigma_1 , \Gamma , \Delta' , I' , F' \ralg$ , где

$\begin{align*} Q' &= \cala \times Q ,\\ I' &= \{ \varepsilon \} \times I ,\\ F' &= \{ \varepsilon \} \times F ,\\ \Delta' &= \{ \lp \lp \lp \varepsilon , p \rp , a , \varepsilon \rp , \lp \lp h ( a ) , p \rp , \varepsilon \rp \rp \mid a \in \Sigma_1 \commaand p \in Q \} \cup {} \\ &\myqquad \cup \{ \lp \lp \lp x w , p \rp , \varepsilon , \beta \rp , \lp \lp w , q \rp , \gamma \rp \rp \squeeze{\mid} \lp \lp p , x , \beta \rp , \lp q , \gamma \rp \rp \squeeze{\in} \Delta \commaand x w \squeeze{\in} \cala \} . \end{align*}$

Пример 11.2.5. Пусть $\Sigma_1 = \{ c , d , e \}$ и $\Sigma_2 = \{ a , b \}$ . Рассмотрим гомоморфизм $h \colon \Sigma_1^* \farrow \Sigma_2^*$ , заданный равенствами h(c) = aa, h(d) = b и h(e) = bba. Пусть контекстно-свободный язык L распознается МП-автоматом $\lalg Q , \Sigma_2 , \Gamma , \Delta , I , F \ralg$ , где Q = {p}, $\Gamma = \{ A \}$ , I = {p}, F = {p},

$\Delta = \{ \lp \lp p , a , \varepsilon \rp , \lp p , A \rp \rp ,\ \lp \lp p , b , A \rp , \lp p , \varepsilon \rp \rp \} .$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F=]{p} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{a,\varepsilon:A} \rloop{0,-1} ^{b,A:\varepsilon} }$

Тогда язык h^-1(L) распознается МП-автоматом $\lalg Q' , \Sigma_1 , \Gamma , \Delta' , I' , F' \ralg$ , где $Q' = \{ p_{\varepsilon} , p_{a} , p_{aa} , p_{b} , p_{ba} , p_{bba} \}$ , $I' = \{ p_{\varepsilon} \}$ , $F' = \{ p_{\varepsilon} \}$ и

$\begin{align*} \Delta' &= \{ \lp \lp p_{\varepsilon} , c , \varepsilon \rp , \lp p_{aa} , \varepsilon \rp \rp ,\ \lp \lp p_{\varepsilon} , d , \varepsilon \rp , \lp p_{b} , \varepsilon \rp \rp ,\ \lp \lp p_{\varepsilon} , e , \varepsilon \rp , \lp p_{bba} , \varepsilon \rp \rp ,\ \\ &\hphantom{ {} = {} \{ } %\} \lp \lp p_{a} , \varepsilon , \varepsilon \rp , \lp p_{\varepsilon} , A \rp \rp ,\ \lp \lp p_{aa} , \varepsilon , \varepsilon \rp , \lp p_{a} , A \rp \rp ,\ \lp \lp p_{b} , \varepsilon , A \rp , \lp p_{\varepsilon} , \varepsilon \rp \rp ,\ \\ &\hphantom{ {} = {} \{ } %\} \lp \lp p_{ba} , \varepsilon , A \rp , \lp p_{a} , \varepsilon \rp \rp ,\ \lp \lp p_{bba} , \varepsilon , A \rp , \lp p_{ba} , \varepsilon \rp \rp \} . \end{align*}$

$\objectwidth={7.5mm} \objectheight={7.5mm} \let\objectstyle=\scriptstyle \xymatrix @=11mm{ % & *=[o][F-]{p_{aa}} \ar "1,3" ^{\varepsilon,\varepsilon:A} & *=[o][F-]{p_{a}} \ar "2,4" _{\varepsilon,\varepsilon:A} & \\ *=[o][F-]{p_{bba}} \ar "2,2" ^{\varepsilon,A:\varepsilon} & *=[o][F-]{p_{ba}} \ar "1,3" _{\varepsilon,A:\varepsilon} & & *=[o][F=]{p_{\varepsilon}} \ar @`{+/l16mm/} [] ^{} \ar `u^l{[-1,-2]+/u9mm/}_{c}`l^d{[-1,-2]} "1,2" \ar `d_l{[1,-1]}^-{d} "3,3" \ar `r_d{+/r7mm/}`d_l{[1,-1]+/d7mm/}^{e}`l_u{[0,-3]} "2,1" \\ % & & *=[o][F-]{p_{b}} \ar "2,4" ^{\varepsilon,A:\varepsilon} & }$

Язык h^-1(L) также порождается контекстно-свободной грамматикой 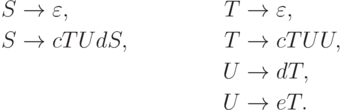$\begin{align*} S \; & {\to} \; \varepsilon , & T \; & {\to} \; \varepsilon , \\ S \; & {\to} \; cTUdS , & T \; & {\to} \; cTUU ,\\ & & U \; & {\to} \; dT , \\ & & U \; & {\to} \; eT . \end{align*}$

Упражнение 11.2.6. Пусть гомоморфизм $h \colon \{a,b,c\}^* \farrow \{a,b\}^*$ задан соотношениями h(a) = ab, h(b) = aaba, h(c) = b. Рассмотрим язык L, порождаемый грамматикой

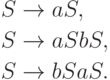
$\begin{align*} S \; & {\to} \; a S , \\ S \; & {\to} \; a S b S , \\ S \; & {\to} \; b S a S . \end{align*}$

Описать язык h^-1(L).

Упражнение 11.2.7. 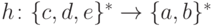$h \colon \{c,d,e\}^* \farrow \{a,b\}^*$ задан соотношениями h(c) = a, h(d) = ba, h(e) = bb. Рассмотрим язык L, порождаемый грамматикой

$\begin{align*} B \; & {\to} \; a B B a , \\ B \; & {\to} \; b . \end{align*}$

Найти контекстно-свободную грамматику для языка h^-1(L).

Упражнение 11.2.8. Пусть гомоморфизм 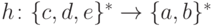$h \colon \{c,d,e\}^* \farrow \{a,b\}^*$ задан соотношениями h(c) = bba , h(d) = aa , h(e) = b . Рассмотрим язык , порождаемый грамматикой

$\begin{align*} S \; & {\to} \; a S b S , \\ S \; & {\to} \; \varepsilon . \end{align*}$

Найти контекстно-свободную грамматику для языка h^-1(L).

Упражнение 11.2.9. Обозначим через L язык, порождаемый грамматикой

$\begin{align*} S \; & {\to} \; a S b , \\ S \; & {\to} \; ba . \end{align*}$

Рассмотрим гомоморфизм $h_1 \colon \{a,b,c,d,e,f\}^* \farrow \{a,b,c\}^*$ , заданный соотношениями

h₁(a) = ac ,
 h₁(b) = bc ,
 h₁(c) = aa ,
 h₁(d) = ab ,
 h₁(e) = ba ,
 h₁(f) = bb ,

и гомоморфизм $h_2 \colon \{a,b,c,d,e,f\}^* \farrow \{a,b\}^*$ , заданный соотношениями

h₂(a) = a ,
 h₂(b) = b ,
 h₂(c) = ab ,
 h₂(d) = aa ,
 h₂(e) = bb ,
 h₂(f) = ba .

Найти контекстно-свободную грамматику, порождающую язык

$h_2(h_1^{-1}( L \cdot \{ \varepsilon , c \} )) .$

Дальше >>

Авторизоваться

Математическая теория формальных языков

Дополнительные свойства контекстно-свободных языков

11.2. Гомоморфизмы и контекстно-свободные языки

Вопросы и ответы