НОУ ИНТУИТ | Разработка приложений для мобильных интеллектуальных систем на платформе Intel Atom. Лекция 5: Мультиагентное управление

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Санкт-Петербургский государственный университет

Опубликован: 12.07.2013 | Доступ: свободный | Студентов: 246 / 38 | Длительность: 09:36:00

Темы: Программирование, Мобильные технологии

Специальности: Программист

Теги: android, java, мобильные технологии, разработка приложений, системы программирования

|

Вам нравится? Нравится 12 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Задача балансировки загруженности сети

В последнее время все чаще при вычислениях используются распределенные системы параллельных вычислений, для которых актуальна задача разделения пакета заданий между несколькими вычислительными устройствами.

Рассмотрим модель системы разделения однотипных заданий между разными узлами для параллельных вычислений с обратной связью. Обозначим $N= \lbrace 1,…,n \rbrace$ набор интеллектуальных агентов (вычислительных узлов), каждый из которых обслуживает поступающие заявки на вычисления по принципу очереди, то есть первый вошел - первый вышел. Будем считать, что всем агентам присылают однотипные задания, которые можно раздробить на одинакове по сложности атомарные единицы. Задания поступают в различные моменты времени и на разные узлы. Считается известным размер каждой задачи (или задания), то есть его трудоемкость, в секундах или циклах процессора.

В каждый момент времени состояние агента , i=1,…,n , описывается двумя характеристиками:

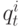– длина очереди из атомарных элементарных заданий в момент времени
– производительность узла (количество (или доля) выполненых атомарных заданий за предшествующий такт времени, при условии полной загрузки).

Обозначим x^i_t=q^i_t / p^i_t

Задача для сети агентов – выполнять поступающие последовательно задания. Будем рассматривать две постановки задачи: стационарную и нестационарную.

Для начала предположим, что все задания поступают в систему на разные узлы в начальный момент времени. Если все задания выполняются только тем агентом, которому они поступили, и производительности агентов не изменяются со временем, то время выполнения всех заданий определяется так: . Для минимизации времени выполнния всех заданий при возможности их перераспределения между агентами естественно рассматривать задачу оптимизации загрузки сети.
При тех же предположениях задача оптимизации загрузки остается актуальной и при поступлении в сеть новых заданий с течением времени. Новые задачи могут поступить прямо на любой из узлов. Каждый узел в определенный момент времени "видит" только соседей из множества . При этом считаем, граф связности полный, т. е. из каждого узла существует цепочка в любой другой. Динамики изменений каждого из узлов при неизменных производительностях описываются следующими уравнениями
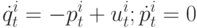
$\dot {q}^i_t=-p^i_t+u^i_t;\\ \dot{p}^i_t=0$ ( 6)

В каждый момент времени узел может получить от своих "видимых" соседей $j \in N^i_t$ следующую информацию:

наблюдения о том, какова его загрузка $y^{-ij}_t$ ;
– производительность узла.

Задача состоит в том, чтобы составить протокол общения между агентами, при котором все узлы будут загружены равномерно, т. е. 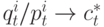$q^i_t/p^i_t \rightarrow c^*_t$ , независящей от , т. е. если в систему не будут поступать новые заказы, то все узлы закончат работать одновременно.

На рис. 9.1 приведен пример вычислительной сети из шести агентов с указанием возможных каналов связи, часть из которых может "закрываться" и "открываться" с течением времени.

Рис. 9.1. Максимальное множество каналов связи

Протоколы консенсуса

В 6 показано, что консенсус асимптотически достижим в двух типичных случаях.

Для фиксированной или меняющейся топология и нулевом времени задержки связи при линейном протоколе консенсуса:
$u^i_t=\sum \limits_{j \in N^i_t} a^{i,j} (x^j_t - x^i_t)$ ( 7)
где множество соседей узла меняются в сети с переменной топологией.
Для фиксированной топологии и задержкам по времени связи $d^{ij}_t > 0$ , соответствующим ребрам $i,j \in E$ при линейном протоколе консенсуса с задержной по времени связи:
$u^i_t=\sum \limits_{j \in N^i_t} a^{i,j} (x^j_{t-d^{ij}_t} - x^i_{t-d^{ij}_t})$ ( 8)

В случае неориентированных графов для интуитивного обоснования протокола (7) можно воспользоваться следующими соображениями. Определим потенциал Лапласа , связанный с неориентированным графом G=(N,E,A) следующим образом:

$\Phi_G(X_t)=1/2 \sum \limits^n_{i,j=1}a^{i,j}(x^j_t-x^i_t)^2,$

( 9)

и отметим, что обратная связь, основанная на методе скоростного градиента 25 $u_t=-1/2 \bigtriangledown \Phi_G(X_t)$ совпадает с протоколом (7). В результате динамика сети для агентов с применением протокола (7) выглядит следующим образом:

$\dot {X}_t=-1/2\bigtriangledown \Phi_G(X_t)$

( 10)

, которая является градиентной системой порожденной графом .

Для ориентированных сетей вопрос об обосновании протокола консенсуса является более сложным.

Обычно рассматривают два типа протоколов консенсуса, которые решают задачу согласования в сети с непрерывным временем для агентов с динамикой:

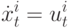$\dot {x}^i_t=u^i_t$

( 11)

или для модели агентов в дискретном времени:

$x^i_{t+1}=x^i_t+\alpha u^i_t$

( 12)

, с некоторым размером шага $\alpha$ > 0 . Мы далее будем рассматривать только дискретный случай.

Для решения сформулированной в разделе 2 общей постановки задачи о построениии протокола консенсуса в 12 предлагается следующий метод стохастической аппроксимации.

Определим матрицу $B_t=(b^{i,k}_t)_{1 \leqslant i , k \leqslant n }$ следующим образом: если $N^i_t= \varnothing$ , то

$b^{i,k}_t=0$

( 13)

для любого $k \in N$ . Если $N^i_t \neq \varnothing$ , то

$\begin{cases} b^{i,k} \in [ \underline {b}, \overline {b}], k \in N^i_t\\ b^{i,k}=0, k \notin N^i_t \cup \lbrace i \rbrace\\ b^{i,i}_t=-\sum \limits_{k \in N^i_t} b^{i,k}_t \end{cases}$

( 14)

где $0 < \underline {b} \leqslant \overline {b} < \propto$ – две детерминированных константы. Пока последовательность $\lbrace G_t \rbrace _{t \geqslant 0$ меняется случайно, $\lbrace B_t \rbrace _{t \geqslant 0$ – матричный случайный процесс.

В момент времени $t \geqslant 0$ , если $N^i_t = \varnothing$ , множество $x^i_{t+1}=x^i_t$ .

Если $N^i_t \neq \varnothing$ , узел меняет свое состояние по правилу:

$x^i_{t+1}=[1+\alpha_t b^{i,j}_t]x^i_t+\alpha \sum \limits_{k \in N^i_t} b^{i,k}_t y^{ik}_t, t \geqslant 0,$

( 15)

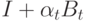где $\lbrace \alpha_t \rbrace _{t \geqslant 0$ – последовательность положительных размеров шагов. Будем называть $I+ \alpha_t B_t$ – весовой матрицей. Поскольку все узлы обновляют свои состояния одновременно, (15) является синхронным алгоритмом.

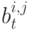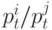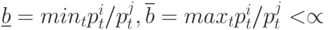Вернемся к задаче о балансировке загрузки узлов вычислительной сети. В качестве ненулевых $b^{i,j}_t$ берем p^i_t/p^j_t . В этом случае $\underline {b}=min_t p^i_t/p^j_t, \overline {b}= max_t p^i_t/p^j_t < \propto$ .

Алгоритм (15) в задаче о балансировке загрузки узлов вычислительной сети принимает вид

$q^i_{t+1}=[1+ \alpha_t b^{i,i}]q^i_t+ \alpha_t \sum \limits_{j \in N^i_t} b^{i,j}y^{-ij}_t, t \geqslant 0,$

( 16)

Задачи балансировки загрузки встречаются не только в вычислительных сетях, но также в производственных, логистических, транспортных и других сетях 33-37.

Дальше >>

Авторизоваться

Разработка приложений для мобильных интеллектуальных систем на платформе Intel Atom

Мультиагентное управление

Задача балансировки загруженности сети

Протоколы консенсуса

Вопросы и ответы