Квантовые вероятности
Перейдем теперь к обсуждению некоторых "физических" аспектов квантовых вычислений. Пусть система из  q-битов находится в состоянии
q-битов находится в состоянии  . Коэффициенты разложения по выделенному базису (классических состояний) называются амплитудами. Квадрат модуля амплитуды
. Коэффициенты разложения по выделенному базису (классических состояний) называются амплитудами. Квадрат модуля амплитуды  равен вероятности обнаружить систему в состоянии
равен вероятности обнаружить систему в состоянии  (сравните с (8.1)). Другими словами, при измерении состояния этой квантовой системы будут получаться классические состояния, распределенные как
(сравните с (8.1)). Другими словами, при измерении состояния этой квантовой системы будут получаться классические состояния, распределенные как  .
.
Определенная формулой (8.1) величина обладает основными свойствами обычной вероятности. Тот факт, что квадрат модуля амплитуды — это вероятность наблюдения системы в состоянии  , согласуется с тем, что физические состояния в квантовой механике соответствуют векторам единичной длины, а преобразования этих состояний не меняют длины, т.е. унитарны. Действительно,
, согласуется с тем, что физические состояния в квантовой механике соответствуют векторам единичной длины, а преобразования этих состояний не меняют длины, т.е. унитарны. Действительно,  (сумма вероятностей равна 1), а применение физически реализуемого оператора должно сохранять это соотношение, т.е. должно быть унитарным.
(сумма вероятностей равна 1), а применение физически реализуемого оператора должно сохранять это соотношение, т.е. должно быть унитарным.
Формулы (8.1) достаточно для определения квантового вычисления и класса BQP. Однако есть вопросы, в которых это определение оказывается неудобным или неприменимым. Два основных примера: измеряющие операторы и алгоритмы, построенные на их основе, и задача построения надежных квантовых схем из ненадежных элементов (исправление ошибок).
Поэтому мы построим определение квантовой вероятности, в котором обобщается как то, что мы наблюдаем (состояние системы), так и результат наблюдения. К этому общему определению мы придем, рассматривая ряд примеров. Для начала перепишем уже полученное выражение для вероятности в виде

 обозначен проектор на подпространство, порожденное
обозначен проектор на подпространство, порожденное  .
.Чтобы сделать следующий шаг к общему определению квантовой вероятности, подсчитаем вероятность того, что первые  битов имеют заданное значение
битов имеют заданное значение 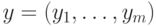 . Для этого представим состояние в виде двух блоков
. Для этого представим состояние в виде двух блоков .
.
Имеем
![\begin{multline*}
\hskip-2pt
\PP(\ket\psi, y)=%\\=
\sum_{z}^{}\PP(\ket\psi,(y,z))
=\sum_{z}^{}\langle \psi\big|\, |y,z\rangle \langle y,z|
\big|\psi\rangle = \langle \psi\big|\, |y\rangle \langle y|\otimes
I\big| \psi\rangle =\\[-2pt]
=\langle \psi|\Pi_\calM|\psi\rangle.
\label{кв-вер-проектор}\index{Квантовая вероятность!для чистого состояния}
\end{multline*}](/sites/default/files/tex_cache/d14a70533e1aefe61d6f616a23c4e30c.png) |
( 9.1) |
 здесь обозначает проектор на подпространство
здесь обозначает проектор на подпространство 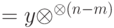 . Формула (9.1) задает определение квантовой вероятности и в том случае, когда
. Формула (9.1) задает определение квантовой вероятности и в том случае, когда  — произвольное подпространство.
— произвольное подпространство.
В этом случае проектор на подпространство  определяется как
определяется как  , где
, где  пробегают любой ортонормированный базис
пробегают любой ортонормированный базис  .
.
Замечание 9.1. Величина  , которая используется в определении вычисления функции из
, которая используется в определении вычисления функции из  в
в  квантовой схемой (см.
"Определение квантового вычисления. Примеры"
), равна
квантовой схемой (см.
"Определение квантового вычисления. Примеры"
), равна  , где
, где  . Еще раз напомним смысл этого определения: схема
. Еще раз напомним смысл этого определения: схема  вычисляет
вычисляет 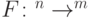 , если для любого
, если для любого  вероятность наблюдения правильного ответа
вероятность наблюдения правильного ответа  после применения схемы к начальному состоянию
после применения схемы к начальному состоянию  больше
больше  .
.
Проекторы не являются физически реализуемыми операторами, точнее говоря, они не описывают переход от одного состояния системы к другому за определенный промежуток времени. Такой переход описывается унитарными операторами. Все же, допуская некоторую вольность, проекторам можно придать физический смысл. Проектор выделяет часть состояний системы из всех возможных. Представьте фильтр (устройство, а не теоретико-множественное понятие), который пропускает только системы в состояниях из  . Если на такой фильтр подать систему в состоянии
. Если на такой фильтр подать систему в состоянии 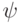 , то сквозь фильтр пройдет система в состоянии
, то сквозь фильтр пройдет система в состоянии 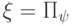 . Суммарная вероятность выделенных состояний, вообще говоря, меньше 1, она равна
. Суммарная вероятность выделенных состояний, вообще говоря, меньше 1, она равна 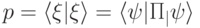 . Число
. Число  определяет вероятность того, что система сквозь фильтр не пройдет.
определяет вероятность того, что система сквозь фильтр не пройдет.
Сравним свойства классической и квантовой вероятности.
Заметим, что условие  эквивалентно условию
эквивалентно условию  .
.
Если есть два неортогональных подпространства с пустым пересечением, то квантовая вероятность необязательно аддитивна. Приведем простой пример, когда  .
.
Пусть  ,
,  (линейное подпространство, порожденное вектором
(линейное подпространство, порожденное вектором  ),
),  , причем
, причем  близко к 1. Тогда
близко к 1. Тогда

Итак, мы определили в наиболее общем виде то, что мы измеряем. Теперь нужно обобщить то, над чем проводится измерение. В результате получим определение вероятности, обобщающее как классическую, так и квантовую вероятность.
Рассмотрим распределение вероятностей на конечном множестве квантовых состояний  . Вероятность состояния
. Вероятность состояния  обозначим
обозначим  , очевидно, что
, очевидно, что 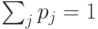 . Подсчитаем вероятность наблюдения состояния в подпространстве
. Подсчитаем вероятность наблюдения состояния в подпространстве  :
:
 |
( 9.2) |
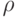 обозначена матрица плотности1В действительности это оператор, а не матрица, однако название "матрица плотности" уже стало традиционным. Впрочем, в дальнейшем мы часто будем иметь в виду именно матрицу, т.е. оператор, записанный в выделенном базисе.
обозначена матрица плотности1В действительности это оператор, а не матрица, однако название "матрица плотности" уже стало традиционным. Впрочем, в дальнейшем мы часто будем иметь в виду именно матрицу, т.е. оператор, записанный в выделенном базисе.
 . Последнее выражение в (9.2) и примем за общее определение вероятности.
. Последнее выражение в (9.2) и примем за общее определение вероятности.
 — подмножество некоторого конечного множества.
— подмножество некоторого конечного множества.  со свойствами а)
со свойствами а) 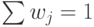 ; б)
; б)  . Вероятность:
. Вероятность:  .
. .
.  . Вероятность:
. Вероятность: 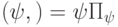 .
. , то
, то 
 .
.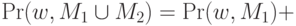
 .
. , то
, то  .
.