Лемма Цорна и свойства операций
Лемма Цорна и ее применения
В современных учебниках редко встречается трансфинитная индукция как таковая: она заменяется ссылкой на так называемую лемму Цорна. Сейчас мы покажем, как это делается, на примере теоремы о существовании базиса в линейном пространстве.
Теорема 30 (лемма Цорна)
Пусть  - частично упорядоченное множество, в
котором всякая цепь имеет верхнюю границу. Тогда в этом
множестве есть максимальный элемент, и, более того, для любого
элемента
- частично упорядоченное множество, в
котором всякая цепь имеет верхнюю границу. Тогда в этом
множестве есть максимальный элемент, и, более того, для любого
элемента  существует элемент
существует элемент  ,
являющийся
максимальным в
,
являющийся
максимальным в  . ( Цепь - это подмножество,
любые два элемента
которого сравнимы. Верхняя граница цепи - элемент, больший или
равный любого элемента цепи.)
. ( Цепь - это подмножество,
любые два элемента
которого сравнимы. Верхняя граница цепи - элемент, больший или
равный любого элемента цепи.)
Доказательство.
Прежде всего отметим, что  лишь частично упорядочено, поэтому
надо различать максимальные и наибольшие элементы. По этой же
причине мы вынуждены употреблять грамматически некорректную
конструкцию " больший или равный любого (любому?)", поскольку
сказать " не меньше любого" (стандартный выход из
положения) означало бы изменить смысл.
лишь частично упорядочено, поэтому
надо различать максимальные и наибольшие элементы. По этой же
причине мы вынуждены употреблять грамматически некорректную
конструкцию " больший или равный любого (любому?)", поскольку
сказать " не меньше любого" (стандартный выход из
положения) означало бы изменить смысл.
Доказательство повторяет рассуждения при построении базиса,
но в более общей ситуации (теперь у нас не линейно независимые
семейства, а произвольные элементы  ).
).
Пусть дан произвольный элемент  . Предположим, что не
существует
максимального элемента, большего или равного
. Предположим, что не
существует
максимального элемента, большего или равного  . Это значит,
что для любого
. Это значит,
что для любого  найдется
найдется  . Тогда
. Тогда  и потому
найдется
и потому
найдется  и т.д Продолжая этот процесс достаточно долго, мы
исчерпаем
все элементы
и т.д Продолжая этот процесс достаточно долго, мы
исчерпаем
все элементы  и придем к противоречию.
и придем к противоречию.
Проведем рассуждение аккуратно (пока что мы даже не использовали
условие леммы, касающееся цепей).
Возьмем вполне упорядоченное множество  достаточно
большой мощности (большей, чем мощность
достаточно
большой мощности (большей, чем мощность  ).
Построим строго возрастающую функцию
).
Построим строго возрастающую функцию  по
трансфинитной рекурсии. Ее значение на минимальном элементе
по
трансфинитной рекурсии. Ее значение на минимальном элементе  будет равно
будет равно  . Предположим, что мы уже знаем все ее значения
на всех элементах, меньших некоторого
. Предположим, что мы уже знаем все ее значения
на всех элементах, меньших некоторого  . В силу монотонности
эти значения попарно сравнимы. Поэтому существует их верхняя
граница
. В силу монотонности
эти значения попарно сравнимы. Поэтому существует их верхняя
граница  , которая, в частности, больше или равна
, которая, в частности, больше или равна  .
Возьмем
какой-то элемент
.
Возьмем
какой-то элемент 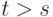 и положим
и положим 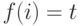 ; по
построению
монотонность сохранится. Тем самым
; по
построению
монотонность сохранится. Тем самым  равномощно
части
равномощно
части  , что
противоречит его выбору.
, что
противоречит его выбору.
В этом рассуждении, формально говоря, есть пробел: мы
одновременно определяем функцию по трансфинитной рекурсии и
доказываем ее монотонность с помощью трансфинитной индукции.
Наше рекурсивное определение имеет смысл, лишь если уже
построенная часть функции монотонна. Формально говоря, надо
воспользоваться теоремой 19,
считая, что следующее значение не определено, если уже
построенный участок не монотонен, и получить функцию,
определенную на всем  или на начальном отрезке. Если она
определена на некотором начальном отрезке, то она монотонна на
нем по построению, поэтому следующее значение тоже определено -
противоречие.
или на начальном отрезке. Если она
определена на некотором начальном отрезке, то она монотонна на
нем по построению, поэтому следующее значение тоже определено -
противоречие.
Как и при построении базиса Гамеля
(задача 115), можно обойтись без множества большей
мощности. Вполне упорядочим множество  с помощью теоремы Цермело.
Этот порядок никак не связан с исходным порядком на
с помощью теоремы Цермело.
Этот порядок никак не связан с исходным порядком на  ; мы будем
обозначать
его символом
; мы будем
обозначать
его символом  . Построим с помощью трансфинитной рекурсии
функцию
. Построим с помощью трансфинитной рекурсии
функцию  с такими свойствами:
(1)
с такими свойствами:
(1)  для любого
для любого 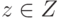 ;
(2)
;
(2)  монотонна в следующем смысле: если
монотонна в следующем смысле: если  , то
, то  ;
(3)
;
(3)  не может быть строго меньше
не может быть строго меньше 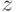 (в смысле
исходного порядка
(в смысле
исходного порядка 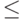 )
ни при каком
)
ни при каком 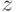 .
.
Делается это так. Значение 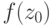 для
для  -
наименьшего
элемента
-
наименьшего
элемента  мы положим равным либо
мы положим равным либо  ,
либо
,
либо  (последнее - если
(последнее - если  ). Значение
). Значение  для
остальных
для
остальных 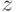 есть либо верхняя граница значений
есть либо верхняя граница значений 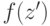 при
при  (по предположению
индукции множество таких значений линейно
упорядочено и потому имеет некоторую верхнюю
границу
(по предположению
индукции множество таких значений линейно
упорядочено и потому имеет некоторую верхнюю
границу  ), либо само
), либо само 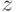 (последнее -
если
(последнее -
если  ).
).
В силу монотонности множество значений функции  линейно
упорядочено и имеет верхнюю границу. Эта граница (обозначим
ее
линейно
упорядочено и имеет верхнюю границу. Эта граница (обозначим
ее 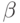 ) больше или равна
) больше или равна  (которое
есть
(которое
есть 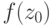 ) и
является искомым максимальным элементом: если
) и
является искомым максимальным элементом: если  для
некоторого
для
некоторого 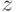 , то
, то  , что
противоречит
свойству (3).
, что
противоречит
свойству (3).
Теперь повторим доказательство теоремы о базисе, используя лемму Цорна.
Пусть 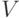 - произвольное векторное пространство.
Рассмотрим частично упорядоченное множество
- произвольное векторное пространство.
Рассмотрим частично упорядоченное множество  , состоящее из
линейно независимых подмножеств пространства
, состоящее из
линейно независимых подмножеств пространства 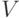 . Порядок
на
. Порядок
на  задается отношением "быть подмножеством".
задается отношением "быть подмножеством".
Проверим, что условия леммы выполнены. Пусть имеется некоторая цепь, то есть семейство линейно независимых множеств, причем любые два множества этого семейства сравнимы. Объединим все эти множества и покажем, что полученное множество будет линейно независимым (тем самым оно будет верхней границей элементов цепи). В самом деле, нетривиальная линейная комбинация включает в себя какое-то конечное число векторов, каждый из своего множества. Этих множеств конечное число, и потому среди них есть наибольшее по включению (в конечном линейно упорядоченном множестве есть наибольший элемент). Это наибольшее множество содержит все векторы нетривиальной линейной комбинации, и линейно независимо по предположению, так что наша нетривиальная линейная комбинация отлична от нуля.
Таким образом, можно применить лемму Цорна и заключить, что любое линейно независимое множество векторов содержится в максимальном линейно независимом множестве векторов. К нему уже нельзя добавить ни одного вектора, не создав линейной зависимости, и оно является искомым базисом.
Аналогичным образом можно доказать существование ортогонального базиса в гильбертовом пространстве (там определение базиса другое: разрешаются бесконечные линейные комбинации, понимаемые как суммы рядов) или существование базиса трансцендентности (максимальная алгебраически независимая система элементов в расширении полей).
Мы приведем другой пример применения леммы Цорна, где фигурируют уже известные нам понятия.
