Графы и способы их представления

Способы описания графов

Теоретико-множественное представление графов

Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 1.3 и рис. 1.4.

G₄ = (Х, А),

где Х = {х_i}, i = 1, 2, 3, 4 – множество вершин; А = {a_i }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х₁, х₂), (х₄, х₂), (х₂, х₄ ), (х₂, х₃), (х₃, х₃), (х₄ , х₁)}.

Рис. 1.3.

G₅ = (X, A),

где X = {B, C, D, E, F} – множество вершин графа, A = {a_i}, i = 1, 2, ..., 5 – множество дуг графа, причем a₁ = (F, B), a₂ = (F, D), a₃ = (B, E), a₄ = (E, C), a₅ = (C, D).

Рис. 1.4.

Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.

Соответствием Г называется отображение множества Х в Х, а граф в этом случае обозначается парой G = (X, Г).

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i, т. е. .

Так для орграфа на рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:

G₄=(X, Г),

где X = {х_i}, i = 1, 2, ..., 4 – множество вершин, Г(х₁) = { х₂ }, Г(х₂) = { х₃, х₄ }, Г(х₃) = { х₃ }, Г(х₄) = { х₁, х₂ } – отображения.

Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 1.2,б Г(х₂) = { х₁, х₃, х₅ }, Г(х₄) ={ х₃, х₅} и т. д.

Матричное представление графов

Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций.

Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа ), однозначно представляющая его структуру.

A = {a_ij}, i, j = 1, 2, ..., n, а каждый элемент матрицы определяется следующим образом:

a_ij = 1, если дуга (х_i, х_j),

a_ij = 0, если нет дуги (х_i, х_j).

Если элемент на диагонали (i=j) равен единице, значит, вершина i имеет петлю.

Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа. Обозначается матрица инциденций B = {b_ij}, i = 1, 2, ..., n, j = 1, 2, ..., m .

Каждый элемент матрицы определяется следующим образом:

b_ij = 1, если х_i является начальной вершиной дуги a_j,

b_ij = –1, если х_i является конечной вершиной дуги a_j,

b_ij = 0, если х_i не является концевой вершиной дуги a_j или если a_j является петлей.

Таким образом, нулевой столбец j в матрице инциденций свидетельствует о том, что дуга a_j яляется петлей.

На рис. 1.5, а,б приведен граф и его матрица смежности, по которой можно найти характеристики вершин. Так сумма элементов i -ой строки матрицы дает полустепень исхода вершины х_i, а сумма элементов i -го столбца дает полустепень захода вершины х_i. По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i -ю строку матрицы. Если элемент a_ij=1, то элемент графа х_j входит в отображение Г(х_i). Например, во 2-й строке матрицы А ( рис. 1.5,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х₂) = { х₂, х₅}.

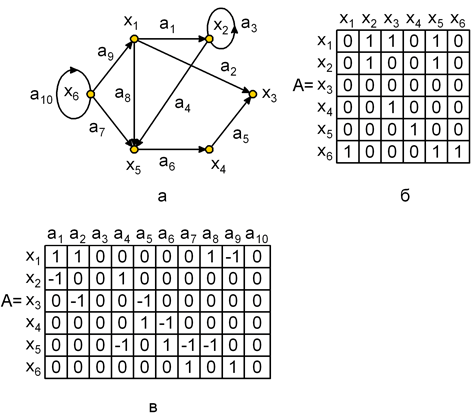
Рис. 1.5. Орграф и его матричное представление: а – орграф; б – матрица смежности; в – матрица инциденций

Для графа на рис. 1.5,а матрица инциденций приведена на рис. 1.5,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.

Для неориентированного графа, матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.