Алгоритмы: частично рекурсивные функции
В этом разделе мы изучим алгебраический подход к определению класса вычислимых функций. Каждая вычислимая функция будет получаться из некоторых простейших очевидно вычислимых базисных функций с помощью некоторых операций, вычислимость которых также не вызывает сомнения. Операция, которая дала название этому подходу - рекурсия - это способ задания функции путем определения каждого ее значения в терминах ранее определенных ее значений и других уже определенных функций.
Класс частично рекурсивных функций
Определение рекурсивных функций
Мы будем рассматривать частичные арифметические функции fn(x1, ..., xn): Nn -> N. Здесь верхний индекс n у имени функции f обозначает число ее аргументов ("арность"). Если арность ясна из контекста или несущественна, то этот индекс будем опускать. Определим вначале три оператора, позволяющих по одним функциям получать другие.
Определение 8.1. Суперпозиция. Пусть Fm и f1n,..., fmn - арифметические функции. Скажем, что функция Gn получена из Fm , f1n, ..., fmn с помощью оператора суперпозиции (обозначение: Gn=[Fm;f1n, ..., fmn] ), если для всех наборов аргументов (x1,...,xn)
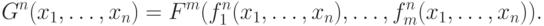
При этом для каждого набора аргументов (a1, ..., an) функция  (т.е. определена), если определены все значения f1n (a1, ..., an)=b1,..., fmn (a1, ..., an)=bm
и
(т.е. определена), если определены все значения f1n (a1, ..., an)=b1,..., fmn (a1, ..., an)=bm
и 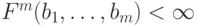 .
.
Определение 8.2. Примитивная рекурсия. Скажем, что функция Fn+1(x1,... ,xn,y) получена с помощью оператора рекурсии из функций gn(x1,..., xn) и hn+2(x1, ..., xn, y, z), если она может быть задана схемой примитивной рекурсии
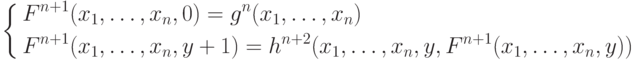
В этом случае будем писать Fn+1 = R(gn,hn+2).
При этом  и для каждого b
и для каждого b
 и
и  .
.
В случае, когда n=0, т.е. F зависит от одного аргумента y, а аргументов x1,...,xn нет, схема примитивной рекурсии принимает вид
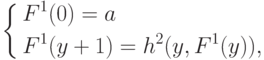
где  .
.
Заметим, что если исходные функции в операторах суперпозиции и примитивной рекурсии всюду определены, то и результирующие функции также всюду определены. Следующий оператор позволяет задавать не всюду определенные, т.е. частичные, функции.
Определение 8.3. Минимизация.
Скажем, что функция Fn(x1,... ,xn) получена с помощью оператора минимизации(  -оператора) из функции gn+1(x1,..., xn,y), если Fn(x1,...,xn)
определена и равна y тогда и только тогда, когда все
значения gn+1(x1,..., xn,0),...,gn+1(x1,..., xn,y-1)
определены и не равны 0, а gn+1(x1,..., xn,y)=0.
В этом случае будем писать
-оператора) из функции gn+1(x1,..., xn,y), если Fn(x1,...,xn)
определена и равна y тогда и только тогда, когда все
значения gn+1(x1,..., xn,0),...,gn+1(x1,..., xn,y-1)
определены и не равны 0, а gn+1(x1,..., xn,y)=0.
В этом случае будем писать
![\ F^n(x_1,\ldots, x_n) =\mu y[ g^{n+1}(x_1,\ldots, x_n,y)=0].](/sites/default/files/tex_cache/0afeaa3154d8e69a1dc4466e2ad3a465.png)
Определение 8.4. Простейшие функции. Функция называется простейшей, если она является одной из следующих функций:
- o1(x)=0 - тождественный нуль;
- s1(x)= x+1 - следующее число (плюс один);
- функции выбора аргумента Imn (x1, ... ,xn)=xm (1 <= m <= n).
Заметим, что все простейшие функции вычислимы в интуитивном смысле. Кроме того, операторы суперпозиции, примитивной рекурсии и минимизации таже вычислимы: понятны алгоритмы, по которым из программ для исходных функций можно получить программы для результирующих. Следующее определение вводит интересующий нас класс частично рекурсивных функций и его важные подклассы.
Определение 8.5. Частично рекурсивные функции. Функция f называется частично рекурсивной функцией (ч.р.ф.), если она является одной из простейших функций или может получиться из них с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и минимизации, т.е. существует последовательность функций f1,f2,..., fn=f, каждая из которых является либо простейшей, либо получена из предыдуших с помощью одного из указанных операторов. Указанная последовательность функций называется частично рекурсивным описанием функции f.
Функция f называется общерекурсивной функцией (о.р.ф.), если она частично рекурсивна и всюду определена.
Функция f называется примитивно рекурсивной функцией (п.р.ф.), если она частично рекурсивна и для нее существует частично рекурсивное описание, использующее лишь операторы суперпозиции и примитивной рекурсии. В таком случае оно называется примитивно рекурсивным описанием функции f.
Нетрудно проверить, что каждая примитивно рекурсивная функция всюду определена, т.е. является общерекурсивной (обратное, вообще говоря, неверно).
Примеры
Приведем некоторые примеры частично рекурсивных функций.
Пример 8.1. Постоянные функции.
Пусть fn(x1,...,xn)=k
для всех наборов аргументов (x1,...,xn) и числа  . Тогда
. Тогда
![f^n\ =\underbrace{ [s^1;[s^1;\ldots[s^1;}_{k \textit{ раз}}[o^1;I^n_1]]]\ldots]].](/sites/default/files/tex_cache/ce87bdd1b77cba7a1fd800518ffc050f.png)
Пример 8.2. Сложение: +2(x,y)=x+y.
Функция сложения определяется следующей примитивной рекурсией.
![\left \{
\aligned x&+0 =x = I^1_1(x) \\
x&+(y+1)=(x+y)+1=[s^1;(x+y)]=[s^1;\ I^3_3(x,y,x+y)]
\endaligned \right .](/sites/default/files/tex_cache/3e798e22a191773fe2b7c5976df74706.png)
Следовательно, +2 =R(I11,[s1;I33]).
Пример 8.3. Умножение: x2(x,y)=x x y.
Используя сложение, умножение можно задать следующей примитивной рекурсией:
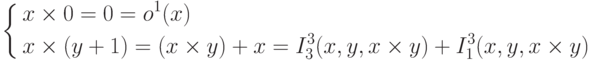
Следовательно, x2 =R(o1,[+;I33,I13]).
Пример 8.4. Минус 1:  .
.
Нетрудно проверить, что  .
.
Пример 8.5. Вычитание :  , если x >= y
и
, если x >= y
и  , если x < y.
, если x < y.
Вычитание определяется следующей примитивно рекурсивной схемой:
![\left \{
\aligned x&\dot{-} 0 =x = I^1_1(x) \\
x&\dot{-} (y+1)=(x\dot{-} y)\dot{-}1=
[\dot{-}1^1;I^3_3(x,y,x\dot{-} y)]
\endaligned \right .](/sites/default/files/tex_cache/7585cae2674f0d6aae99feac1a686a88.png)
Следовательно, ![\dot{-}^2 =R(I^1_1,[\dot{-}1^1;I^3_3])](/sites/default/files/tex_cache/429e0c2f0a8c524eb0ab9f131f0b97f8.png) .
.
Пример 8.6. Предикаты равенства и неравенства нулю:

Примитивная рекурсивность этих функций следует из равенств ![sg=R(0,[s^1;[o^1;I^2_1]])\](/sites/default/files/tex_cache/5b918f1acf64598244215159adc90abd.png) и
и  .
.
Пример 8.7. Модуль разности:  .
.
Пример 8.8. rm(x,y)= остаток от деления y на x (при x=0 положим rm(0,y)=y ).
Заметим, что
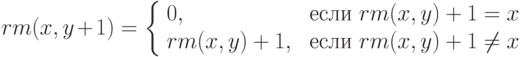
Тогда функцию rm(x,y) можно задать примитивно рекурсивной схемой
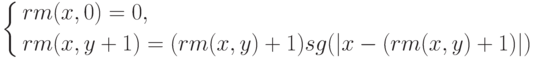
Правую часть второго равенства легко представить как функцию g(x,y,rm(x,y)), полученную с помощью суперпозиции уже построенных примитивно рекурсивных функций.
Пример 8.9. Нигде не определенная функция  .
.
Эта функция может быть задана, например, соотношением ![\omega (x)= mu y[ s^{1}(y)+x=0 ]](/sites/default/files/tex_cache/9ec6b03150497670cb64355ceffe128b.png) .
.
Отметим, что все функции в примерах 8.1 - 8.8 являются примитивно рекурсивными.
