Конечные автоматы: преобразователи и распознаватели

Конечные автоматы - распознаватели

Детерминированные конечные автоматы (ДКА) и автоматные языки

Пусть - это алфавит, который состоит из конечного множества элементов, называемых символами (буквами).

Слово в алфавите 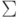- это конечная последовательность символов этого алфавита: при i=1, ..., n . Число букв в этой последовательности называется длиной слова и обозначается |w|. Имеется одно специальное "пустое" слово длины 0. Будем обозначать его через 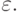На словах определена операция приписывания одного слова после другого, называемая конкатенацией: если слово w =w₁... w_n, а слово v =v₁... v_m, то их конкатенация - это слово w₁... w_nv₁... v_m длины n+m. Обычно знак конкатенации будем опускать и писать просто w v (по аналогии со знаком умножения в алгебре). Пустое слово - это единственное слово такое, что для любого слова w справедливо равенство . Операция конкатенации ассоциативна: для любых трех слов w, v и u, очевидно, имеет место равенство: (w v)u = w(v u). Поэтому скобки при записи конкатенации нескольких слов будем опускать. Для представления нескольких конкатенаций одного и того же слова используют сокращенную "степенную форму" записи: . Например, a³b⁴c² - это сокращенная запись слова aaabbbbcc.

Языком в алфави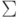те называется произвольное множество слов этого алфавита. Язык, включающий все слова в алфавите 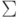( в том числе и пустое слово ), будем обозначать через .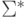

Конечные автоматы часто используются для определения тех или иных свойств слов, т.е. для распознавания языков: автомат, распознающий некоторый язык L должен по произвольному слову w ответить на вопрос " ? ". Для решения такой задачи функция выходов может быть заменена на проверку того, в какое состояние переходит автомат после получения входного слова w - "принимающее" или "отвергающее".

Определение 4.3. Детерминированный конечный автомат (ДКА) - распознаватель - это система вида

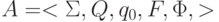
включающая следующие компоненты:

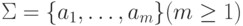• - конечное множество - входной алфавит ;
• Q={q₀, ... , q_n-1} (n >= 1) - конечное множество - алфавит внутренних состояний;
• - начальное состояние автомата;
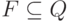• - множество принимающих (допускающих, заключительных) состояний ;
• - функция переходов,
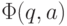• - это состояние, в которое переходит автомат из состояния q, когда получает на вход символ a.

Функцию называют программой автомата A и задают как список из m n команд вида .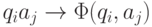

Удобно также задавать функцию с помощью описанной выше таблицы размера n x m, строки которой соответствуют состояниям из Q, а столбцы - символам из входного алфавита и в которой на пересечении строки q_i и столбца a_j стоит состояние .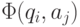

Как и автоматы-преобразователи, автоматы-распознаватели можно представлять с помощью размеченных ориентированных графов, называемых диаграммами.

Определение 4.4. Диаграмма ДКА - это ориентированный (мульти)граф D_A=(Q, E) с помеченными ребрами, в котором выделена вершина- начальное состояние q₀ из каждой вершины 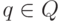выходит 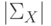ребер, помеченных символами 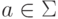так, что для каждой 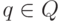и каждого символа 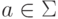имеется единственное ребро из q в вершину 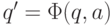с меткой a .

Скажем, что представленный последовательностью ребер путь p=e₁e₂ ... e_t в диаграмме несет слово w=w₁w₂ ... w_t, если w_i - это метка ребра e_i (1 >= i >= t). Если q - начальная вершина (состояние) этого пути, а q' - его заключительная вершина, то будем говорить, что слово w переводит q в q'.

Работа конечного автомата-распознавателя состоит в чтении входного слова и изменению состояний в зависимости от его символов.

Определение 4.5. Назовем конфигурацией ДКА произвольную пару вида (q, w), в которо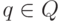й и .

На множестве конфигураций введем отношение перехода за один шаг :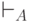

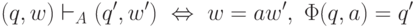
Если , то положим для каждого : .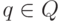

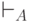
Через обозначим рефлексивное и транзитивное замыкание .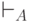

Содержательно, означает, что автомат A, начав работу в состоянии q на слове w=w₁ ... w_l, через некоторое конечное число шагов 0 <= k <= l прочтет первые k символов слова w и перейдет в состояние q', а w' =w_k+1 ... w_l - это непрочтенный остаток слова w.

Определение 4.6. ДКА A распознает (допускает, принимает) слово w, если для некоторого

т.е. после обработки слова w автомат переходит в принимающее состояние.

Язык L_A, распознаваемый (допускаемый, принимаемый) автоматом A, состоит из всех слов, распознаваемых этим автоматом:

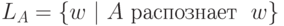
Язык называется конечно автоматным, если он распознается некоторым ДКА.

Из этого определения, в частности, следует, что . Один и тот же язык может распознаваться разными автоматами.

Определение 4.7. Автоматы A и B называются эквивалентными, если совпадают распознаваемые ими языки, т.е. L_A = L_B .

Определение распознавания слова и языка можно легко перевести на язык диаграмм.

Лемма 4.3. Автомат A распознает (допускает, принимает) слово w, если для некоторого в диаграмме D_A имеется путь из q₀ в q, который несет слово w, т.е. w переводит q₀ в заключительное состояние q.

Доказательство можно провести индукцией по длине слова w (см. задачу 4.3).

Tаким образом, язык L_A, распознаваемый автоматом A, состоит из всех слов, которые переводят в его диаграмме D_A начальное состояние q₀ в заключительные состояния из F.

Наша цель теперь состоит в изучении класса конечно автоматных языков.

Во многих случаях удается доказать, что язык L конечно автоматный, непосредственно построив распознающий его автомат. Для этого нужно постараться разбить множество всех входных слов на конечное число классов "однородных", "эквивалентных" слов, т.е. слов, получение которых на входе одинаково влияет на возможность их продолжения до слов распознавемого языка. Затем для каждого такого класса создать состояние автомата и определить переходы между этими состояниями. Часто полезно бывает выделить одно состояние для представления "ошибочных" слов, для которых ни они сами, ни любые их продолжения не входят в язык.