Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3435 / 667 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00
Тема: Математика
Специальности: Математик
Теги:
Практическая работа 13:
Элементы дискретного математического анализа
< Практическая работа 12 || Практическая работа 13 || Практическая работа 14 >
Аннотация: Решение типовых задач дискретного математического анализа, оптимизации, обучение реферированию и Интернет–поиску по этой теме
Ключевые слова: численное решение уравнений, аппроксимация, математическое программирование, интерполяция, численное интегрирование, численное дифференцирование, оптимизация
Задачи
- Найти численно (с точностью 0,01 ) решение уравнения x4-2x-4,5=0. Указание: использовать схему Эйлера.
- Сравнить численное и точное решение задач квадратных уравнений x2–5x+6=0, x2–5x+5,99=0. Указание: первое уравнение решить точно, второе – приближенно, например, методом бисекции.
- Определить некоторую дискретно заданную функцию для 3-х значений аргумента и построить интерполянту по этим данным. Указание: использовать квадратный трехчлен.
- Для задачи 3 решить задачу аппроксимации методом наименьших квадратов и найти аппроксимирующий многочлен первой степени. Сравнить результаты. Указание: использовать сравнить отклонения по модулю.
- Для предыдущей задачи решить задачу аппроксимации методом наименьших квадратов и найти аппроксимирующий многочлен наивысшей возможной степени. Сравнить результаты. Указание: полином наивысшей возможной степени – квадратный трехчлен.
- Решить численно задачу Коши: y’(x)=sin(xy)+y3 , y(1)=0. Оценить погрешность решения. Указание: использовать схему Эйлера.
- Решить численно задачу Коши: y’(x)=xy+y2 , y(0)=y(1)=0. Оценить погрешность решения. Указание: использовать схему Эйлера.
- Героиня гоголевской "Женитьбы" Агафья Тихоновна высказывала: "Право, такое затруднение – выбор. Если бы еще один, два человека, а то четыре. Как хочешь, так и выбирай… Если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности, какая у Балтазара Балтазаровича, да, пожалуй, прибавить к этому еще дородности Ивана Павловича – я бы тогда тотчас же решилась…". Сформулируйте содержательно некоторую оптимизационную задачу на основе этих пожеланий. Указание: это шуточная задача, но можно ее формализовать, введя оценки (веса) привлекательности каждого "претендента" и составив задачу максимизации весов "идеального претендента".
-
Решить графически задачу линейного программирования (указать множество допустимых решений и узловые точки):
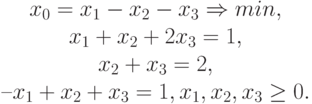
Указание: нарисовать чертеж области в пространстве.
- Решить предыдущую задачу симплекс-методом. Указание: найти начальное, опорное решение.
Темы научных исследований и рефератов (Интернет-листов)
- Роль и значение дискретного анализа в науке (в теории).
- Роль и значение дискретного анализа в практике.
- Интерполяция, ее применение. Методы интерполяции.
- Аппроксимация, ее применения. Методы аппроксимации.
- Численное интегрирование, его применения. Методы численного интегрирования.
- Численное дифференцирование, его применения. Методы численного дифференцирования.
- Основные численные методы решения обыкновенных дифференциальных уравнений.
- Суммирование бесконечных рядов, философский анализ понятия суммы.
- Оптимизация вокруг нас. Методы оптимизации.
- Выбор решения с помощью линейного программирования.
< Практическая работа 12 || Практическая работа 13 || Практическая работа 14 >
