Подпространства линейного пространства. Евклидово пространство. Линейные преобразования в линейном пространстве. Представление линейного преобразования матрицей. Действия над линейными преобразованиями. Примеры линейных преобразований

Линейные преобразования в линейном пространстве

Определение 24. Если некоторая величина характеризуется полностью одним числом, не зависящим от базиса линейного пространства, то такую величину называют скалярной, или скаляром. Скалярная величина обозначается одной буквой, без выделения.

Одним из основных понятий математики является функциональная зависимость. Говорят, что скалярная величина у является функцией скалярного аргумента х, если каждому значению переменной х, взятому из некоторого множества допустимых значений, соответствует определенное значение переменной у. Закон соответствия обычно записывают в виде y = f(x), где f - символическое обозначение некоторой функции.

Функции в общем случае зависят от одного или от нескольких вещественных переменных. Если функция зависит от трех вещественных переменных, то тогда говорят о функции, аргументом которой является вектор пространства V₃.

Поэтому понятие функциональной зависимости можно обобщить на векторные функции от векторного аргумента. Здесь мы ограничимся самыми простейшими типами, к которым относятся линейные функции. Векторные функции являются линейными операторами и обозначаются как y=Ax. С этой точки зрения операции над множествами, приведенные на рис. 7.1 "Линейные пространства и операции над ними. Определения и аксиомы линейного пространства. Следствия из аксиом линейного пространства" , можно рассматривать как примеры линейных операторов: позиция а - операция прибавления числа 5, позиция б - операция вычитания числа 3, позиция в - операция умножения на число 3, т.е. оператор А обозначает правило, по которому элементам множества А ставятся в соответствие элементы множества Б.

Определим два линейных пространства R и R₁ над числовым полем К, и пусть вектор х принадлежит линейному пространству R, а вектор у - линейному пространству R₁.

Определение 25. Оператором А называют любой закон (правило), по которому каждому вектору ставят в соответствие вектор 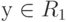и обозначают у = Ах.

Определение 26. Оператор А называют линейным, если выполняются условия: .

Из определения 25 следует, что линейный оператор А определяет преобразование А вектора в вектор 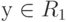. Вектор у называют образом вектора х, а вектор х - прообразом вектора у. Тогда очевидно, что множество L всех образов у = Ах, где , образует подпространство линейного пространства R₁. Действительно, если и , то сумма у₁ + у₂ = Ах₁ + Ах₂ = А(х₁ +х₂) = А(х₃) тоже будет принадлежать L, а при умножении у на имеем , т.е. 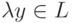, откуда на основании определения 32 следует, что L - является подпространством пространства R₁.

Таким образом, преобразование R в L с помощью линейного оператора А есть отображение пространства R в пространство R₁.