|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Линейная зависимость векторов. Размерность и базис линейного пространства. Линейные операции в координатах
Линейная зависимость векторов. Размерность и базис линейного пространства
Определение 6. Векторы а1, а2, ..., ак линейного пространства называются линейно зависимыми, если существуют такие числа  , не равные одновременно нулю, при которых выполняется:
, не равные одновременно нулю, при которых выполняется:
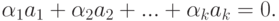 |
( 8.1) |
Определение 7. Если равенство (8.1) выполнимо лишь при всех  , то векторы а1, а2, ..., ак называются линейно независимыми.
, то векторы а1, а2, ..., ак называются линейно независимыми.
Определение 8. Если имеет место равенство  , то говорят, что вектор b является линейной комбинацией векторов а1, а2, ..., ак, или линейно выражается через эти векторы.
, то говорят, что вектор b является линейной комбинацией векторов а1, а2, ..., ак, или линейно выражается через эти векторы.
Заметим, что если векторы а1, а2, ..., ак линейно зависимы, то тогда, по крайней мере, один из векторов может быть линейно выражен через остальные. Это вытекает из самого определения 6, так как, если хотя бы один из  , то на него можно выполнить деление остальных
, то на него можно выполнить деление остальных  и тогда будем иметь
и тогда будем иметь  , где
, где  . Верно и обратное утверждение, что если один из векторов линейно выражается через остальные, то все эти векторы в совокупности линейно зависимы.
. Верно и обратное утверждение, что если один из векторов линейно выражается через остальные, то все эти векторы в совокупности линейно зависимы.
Заметим, что если векторы a и b не коллинеарны или a, b и c не компланарны, то такие векторы являются линейно независимыми соответственно на плоскости или в пространстве.
Покажем это на примере трех некомпланарных векторов a, b и c. Доказательство проведем методом от противного, предположив, что указанные векторы хотя и не компланарны, но линейно зависимы. Тогда должно выполняться условие линейной зависимости векторов, т.е.  и пусть при этом
и пусть при этом  . Тогда на
. Тогда на  можно разделить левую и правую часть уравнения и в результате будем иметь выражение
можно разделить левую и правую часть уравнения и в результате будем иметь выражение 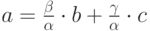 , которое противоречит определению 10 (
""
), т.е. хотя векторы a, b и c не компланарны, но вектор a линейно выражается через два других b и c, что говорит (по определению 8) о их линейной зависимости.
Из этого следует, что вектор a должен быть линейно независим с векторами b и c. Интересно, что в трехмерном пространстве любые четыре пространственных вектора будут линейно зависимыми.
, которое противоречит определению 10 (
""
), т.е. хотя векторы a, b и c не компланарны, но вектор a линейно выражается через два других b и c, что говорит (по определению 8) о их линейной зависимости.
Из этого следует, что вектор a должен быть линейно независим с векторами b и c. Интересно, что в трехмерном пространстве любые четыре пространственных вектора будут линейно зависимыми.
Два ненулевых вектора a и b ортогональны, если они перпендикулярны (проекция вектора a на b и проекция вектора b на a равны нулю). Тогда записывают  . Такие векторы всегда линейно независимы.
. Такие векторы всегда линейно независимы.
Если ненулевые векторы a, b и c попарно ортогональны 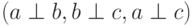 , то тогда они образуют тройку линейно независимых векторов.
, то тогда они образуют тройку линейно независимых векторов.
Определение 9. Рангом системы векторов называется максимальное количество ее линейно независимых векторов.
Определение 10. Линейное пространство называется n -мерным, если в нем можно найти n линейно независимых векторов, а всякая система, состоящая из большего количества векторов, является линейно зависимой в этом пространстве.
Например, векторы, лежащие на одной прямой, образуют одномерное пространство, в котором только один независимый вектор, а все остальные могут быть выражены линейными соотношениями через него. На плоскости множество векторов образует двумерное пространство, т.е. в этом пространстве определены только два независимых вектора.
Определение 11. Если пространство имеет конечное множество линейно независимых векторов, то его называют конечномерным, а если в нем можно найти сколь угодно много линейно независимых векторов, то - бесконечномерным.
Определение 12. Совокупность n линейно независимых единичных векторов n -мерного пространства называют базисом n -мерного пространства.
Заметим, что через базисные векторы могут быть выражены любые другие векторы, определяемые в данном базисе.
Теорема. Каждый вектор х линейного n -мерного пространства можно представить, и притом единственным образом, в виде линейной комбинации векторов базиса.
Доказательство теоремы состоит из двух частей. Сначала мы докажем возможность выразить любой произвольный вектор через базис линейного пространства, а затем, что разложение произвольного вектора по данному базису единственное.
Пусть произвольный базис n -мерного пространства R и некоторый произвольный вектор  . Так как каждые n + 1 векторов n -мерного пространства R линейно зависимы (определение 6), то система, которую образуют векторы l1, l2, ..., ln и x должна быть линейно зависимой. А это значит, что выполняется равенство
. Так как каждые n + 1 векторов n -мерного пространства R линейно зависимы (определение 6), то система, которую образуют векторы l1, l2, ..., ln и x должна быть линейно зависимой. А это значит, что выполняется равенство
 |
( 8.2) |
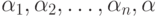 - числа одновременно не равные нулю. При этом ясно, что
- числа одновременно не равные нулю. При этом ясно, что  , так как в противном случае хотя бы одно из чисел
, так как в противном случае хотя бы одно из чисел 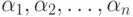 не равнялось бы нулю и тогда равенство (8.2) имело бы вид
не равнялось бы нулю и тогда равенство (8.2) имело бы вид |
( 8.3) |
 коэффициенты при li и перенеся их в правую часть. После выполнения указанных преобразований имеем
коэффициенты при li и перенеся их в правую часть. После выполнения указанных преобразований имеем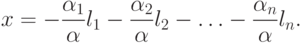
Положим  . Тогда
. Тогда
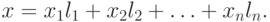 |
( 8.4) |
Докажем теперь, что разложение (8.4) вектора x по данному базису l1, l2, ..., ln единственное. Предположим, что вектор x в пространстве R имеет два различных разложения
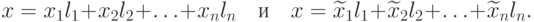
Тогда вычтем из одного равенства другое, и так как в левых частях равенства стоит один и тот же вектор, то получим
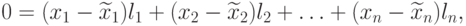

Последнее выражение полностью доказывает теорему.
Определение 13. Числа х1, х2, ..., хn в разложении (8.4) вектора x по базису l1, l2, ..., ln называют координатами вектора в этом базисе и обозначают как х = (х1, х2, ..., хn).
