|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4378 / 711 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00
Тема: Математика
Специальности: Математик
Теги:
Лекция 5:
Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ
Метод Гаусса последовательного исключения неизвестных
Рассмотрим систему m линейных уравнений с n неизвестными
 |
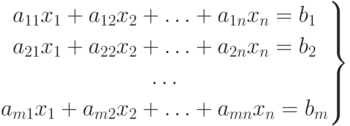( 4.12) |
Элементарными преобразованиями системы (4.12) называют:
- перестановку любых двух уравнений;
- умножение обеих частей любого уравнения на любое число, отличное от нуля;
- прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.
Очевидно, что элементарные преобразования переводят линейную систему в эквивалентную.
Ступенчатой системой называется система линейных уравнений вида
 |
( 4.13) |
где 
. Коэффициенты aii называются главными, или ведущими, элементами системы. Например, система
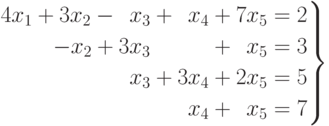
Если в системе (4.13) k = n, то ее называют треугольной. Очевидно, что в этом случае она является определенной.
Если k < n, то k неизвестных х1, х2, ..., хк, называют главными элементами. Они могут быть выражены через остальные n – k неизвестные, называемые свободными. В этом случае система (4.13) будет называться неопределенной.
Вернемся к произвольной системе (4.12) и для определенности будем считать, что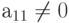 
. Если это не так, то тождественными линейными преобразованиями системы (4.12) можно всегда добиться выполнения данного условия. Исключим х1 из всех уравнений, кроме первого. Для этого обе части первого уравнения умножим на a21/a11 и вычтем из соответствующих частей второго уравнения. Затем обе части первого уравнения умножим на a31/a11
и вычтем из соответствующих частей третьего. И так поступим с каждым следующим уравнением. Далее таким же образом исключаем х2 из третьего, четвертого и так далее уравнений. В результате таких преобразований мы получим совместную ступенчатую систему или придем к несовместимой системе, в которой одно из уравнений имеет отличный от нуля свободный член, а все остальные коэффициенты левой части равны нулю. В последнем случае система (4.12) также будет несовместимой.
Пример 6. Решить систему
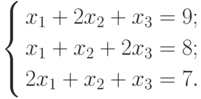
Решение. Вычисления удобно записывать по так называемой схеме единственного деления, в которой оперируют с коэффициентами системы.
| X1 | X2 | X3 | B |  |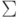
| 1 | 2 | 1 | 9 | 13 |
| 1 | 1 | 2 | 8 | 12 |
| 2 | 1 | 1 | 7 | 11 |
| 1 | 2 | 1 | 9 | 13 |
| 0 | -1 | 1 | -1 | -1 |
| 0 | -3 | -1 | 11 | 15 |
| 1 | 2 | 1 | 9 | 13 |
| 0 | -1 | 1 | -1 | -1 |
| 0 | 0 | -4 | -8 | -12 |
В результате получаем треугольную систему:
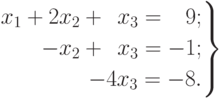
Делая обратный ход, найдем х3 = 2; х2 = 3; х1 = 1, т.е. решение (1, 3, 2).
Замечание. Последний столбец является контрольным. В нем суммируются элементы соответствующих строк.
Арсений Черномаз
