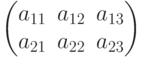|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ
Однородная система трех линейных уравнений с тремя неизвестными
Если в системе (4.2) свободные члены равны нулю, то есть b1 = b2 = b3 = 0, то систему
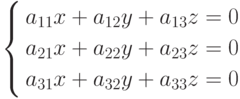 |
( 4.8) |
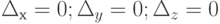 и равенства (4.4) и (4.6) примут вид:
и равенства (4.4) и (4.6) примут вид: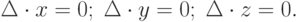 |
( 4.9) |
Если  , то из (4.9) следует, что система (4.8) имеет единственное решение х = 0; y = 0; z = 0. Отсюда следует вывод, что чтобы однородная система (4.8) имела непрерывное решение, необходимо, чтобы
, то из (4.9) следует, что система (4.8) имеет единственное решение х = 0; y = 0; z = 0. Отсюда следует вывод, что чтобы однородная система (4.8) имела непрерывное решение, необходимо, чтобы  . Действительно, если в тройке (х, y, z), например,
. Действительно, если в тройке (х, y, z), например,  , то из равенства
, то из равенства  следует, что
следует, что  .
.
Справедливо и обратное утверждение, т.е. если  , то система (4.8) обязательно имеет ненулевое решение (причем бесчисленное множество).
, то система (4.8) обязательно имеет ненулевое решение (причем бесчисленное множество).
Пусть в системе (4.8) первые два уравнения независимы, а третье является линейной комбинацией первых двух. Тогда система (4.8) равносильна следующей системе двух уравнений с тремя неизвестными
 |
( 4.10) |
Пусть для (10)
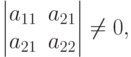
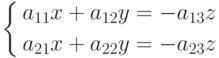
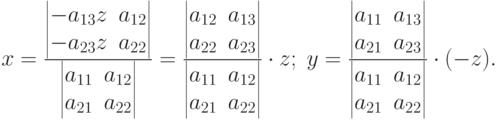
Полагая
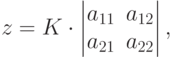
 |
( 4.11) |
Пример 5. Решить систему
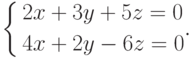
Решение. Так как
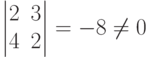
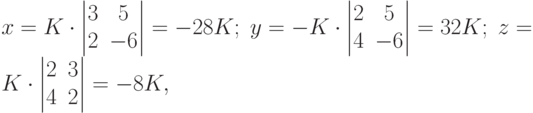
или, вынося общий множитель 4 E={(-7K; 8K; -2K)}.
Замечание. Определители в формулах (4.11) легко запомнить как получить: матрице из коэффициентов системы (4.10)