|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Системы линейных уравнений. Их решение. Системы линейных уравнений. Виды
Основные определения
В общем случае линейная система, составленная из К линейных уравнений относительно n неизвестных примет вид:
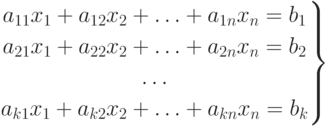 |
( 3.1) |
Определение 1. Решением системы (1) называется совокупность из n чисел (с1, с2, ..., сn), которые, будучи подставленными в систему (1) на место неизвестных x1, x2, ..., xn, обращают все уравнения системы в истинные равенства.
Не всякая система вида (1) имеет решение. Например, очевидно, что система
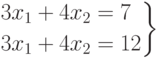
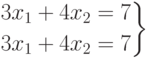
Определение 2. Систему уравнений (1), имеющую хотя бы одно решение, называют совместной, систему, не имеющую решений, - несовместной.
Определение 3. Решения  и
и  считают различными, если хотя бы одно из чисел
считают различными, если хотя бы одно из чисел  не совпадает с соответствующим числом
не совпадает с соответствующим числом 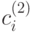 .
.
Например, система
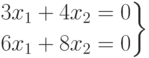
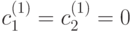 и
и 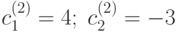 . Системы, имеющие хотя бы 2 различных решения, имеют бесконечное количество разных решений.
. Системы, имеющие хотя бы 2 различных решения, имеют бесконечное количество разных решений.Определение 4. Если совместная система имеет единственное решение, то она называется определенной ; если совместная система имеет по крайней мере два различных решения, то она называется неопределенной.
