НОУ ИНТУИТ | Введение в линейную алгебру. Лекция 2: Определители и их свойства. Определители второго порядка и их свойства. Определители третьего порядка и их свойства. Миноры и алгебраические дополнения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4378 / 711 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

Теги: линейные пространства, метод Гауса, определители, векторы, матрицы

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Миноры и алгебраические дополнения

Рассмотрим определитель третьего порядка

$D= \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}$

( 1.5)

Вычеркнем из определителя одну строку и один столбец, например, первую строку и второй столбец. Из оставшиеся элементов составим определитель второго порядка

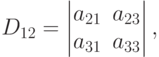
$D_{12}= \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix},$

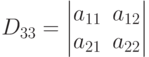
номер которого (индекс у D ) определяется номерами вычеркнутых строки (первой) и столбца (второй). Если из определителя (1.5) вычеркнуть другие строку и столбец, например, третий и третий, соответственно, то оставшиеся элементы будут также составлять определитель второго порядка, номер которого теперь будет другой - $D_{33}= \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}$

Определение 7. Определитель, который получается вычеркиванием одной строки и одного столбца из исходного определителя называется минором основного определителя.

Очевидно, что определитель третьего порядка имеет 9 различных миноров второго порядка, т.е. каждый элемент определителя имеет минор. Если взять определитель, например, пятого порядка, то количество миноров у такого определителя будет 25 – по количеству элементов (5 в строке и 5 столбцов). И эти миноры будут представлены определителями четвертого порядка.

Определение 8. Назовем алгебраическим дополнением любого элемента определителя D минор этого элемента, взятый со знаком плюс, если сумма номеров элемента четная и минус в противном случае

$A_{ij}=(-1)^{i+j}D_{ij}$

( 1.6)

Пример. Выписать и вычислить все алгебраические дополнения определителя $\begin{vmatrix} 1 & 2 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 2 \end{vmatrix}$ .

Решение. У определителя третьего порядка имеется 9 алгебраических дополнений (по каждому из элементов).

$A_{11}=(-1)^{1+1} \begin{vmatrix} 1 & 0 \\ 0 & 2 \end{vmatrix} = 2;$	$A_{21}=(-1)^{2+1} \begin{vmatrix} 2 & 1 \\ 0 & 2 \end{vmatrix} = -4;$
$A_{12}=(-1)^{1+2} \begin{vmatrix} 1 & 0 \\ 1 & 2 \end{vmatrix} = -2;$	$A_{22}=(-1)^{2+2} \begin{vmatrix} 1 & 1 \\ 1 & 2 \end{vmatrix} = 2-1 = 1;$
$A_{13}=(-1)^{1+3} \begin{vmatrix} 1 & 1 \\ 1 & 0 \end{vmatrix} = 0-1=-1;$	$A_{23}=(-1)^{2+3} \begin{vmatrix} 1 & 2 \\ 1 & 0 \end{vmatrix} = -(-2)=2;$
$A_{31}=(-1)^{3+1} \begin{vmatrix} 2 & 1 \\ 1 & 0 \end{vmatrix} = 0-1=-1;$	$A_{32}=(-1)^{3+2} \begin{vmatrix} 1 & 1 \\ 1 & 0 \end{vmatrix} = -(0-1)=1;$
$A_{33}=(-1)^{3+3} \begin{vmatrix} 1 & 2 \\ 1 & 1 \end{vmatrix} = 1-2 =-1$ .

Теорема 1. Определитель D равен сумме произведений элементов любого столбца или строки на их алгебраические дополнения

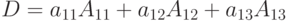$D=a_{11}A_{11}+a_{12}A_{12}+a_{13}A_{13}$

( 1.7)

Очевидно, что для определителя третьего порядка можно записать шесть различных равенств (по трем столбцам и по трем строчкам).

Теорема 2. Суммы, произведений элементов для любого столбца (строки) на алгебраические дополнения другого столбца (строки) определителя, равна нулю.

Доказательство. Проведем доказательство на примере определителя (1.5). Возьмем сумму произведений алгебраических дополнений первой строки на элементы третьей строки. Получим

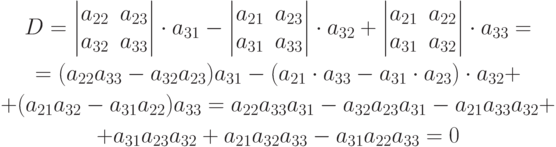
$\begin{gathered} D= \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} \cdot a_{31}- \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix} \cdot a_{32}+ \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix} \cdot a_{33}= \\ =(a_{22}a_{33}-a_{32}a_{23})a_{31}-(a_{21}\cdot a_{33}-a_{31}\cdot a_{23})\cdot a_{32} + \\ +(a_{21}a_{32}-a_{31}a_{22})a_{33}=a_{22}a_{33}a_{31}-a_{32}a_{23}a_{31}-a_{21}a_{33}a_{32}+ \\ +a_{31}a_{23}a_{32} + a_{21}a_{32}a_{33}-a_{31}a_{22}a_{33} = 0 \end{gathered}$

Разложение определителя по строке или столбцу дает нам правило вычисления любых определителей высоких порядков (четвертого и выше).

Определение 9. Определителем n -го порядка называется число $\Delta$ равное алгебраической сумме

$\Delta=a_{11}A_{11}+a_{12}A_{12}+ \cdots +a_{1n}A_{1n},$

( 1.8)

где A_ij=(-1)^i+jD_ij есть алгебраические дополнения элемента a_ij, а D_ij - есть соответствующие миноры, т.е. определители ( n-1 )-го порядка, получающиеся из исходного определителя вычеркиванием первой строки и n -го столбца, на пересечение которых находится элемент a_ij.

Рассмотренные приемы позволяют вычислять определители любых порядков, а, следовательно, находить решение линейных систем любых порядков.

Пример. Вычислить определитель

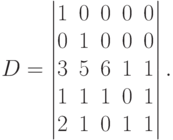
$D= \begin{vmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 3 & 5 & 6 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 \\ 2 & 1 & 0 & 1 & 1 \end{vmatrix}.$

Решение. Для вычисления определителя пятого порядка воспользуемся формулой (1.8) и разложим данный определитель по первой строке (в этой строке все члены, кроме первого равны нулю). Получим

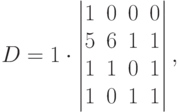
$D=1\cdot \begin{vmatrix} 1 & 0 & 0 & 0 \\ 5 & 6 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{vmatrix},$

т.е. определитель стал теперь четвертого порядка. Опять разложим определитель по первой строке, так как все члены этой строки равны нулю, кроме одного. Затем вычислим полученный определитель третьего порядка по любой вычислительной схеме.

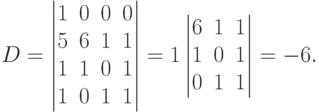
$D= \begin{vmatrix} 1 & 0 & 0 & 0 \\ 5 & 6 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{vmatrix} =1 \begin{vmatrix} 6 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{vmatrix} =-6.$

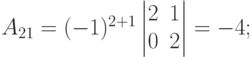
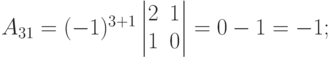
Дальше >>

Авторизоваться

Введение в линейную алгебру

Определители и их свойства. Определители второго порядка и их свойства. Определители третьего порядка и их свойства. Миноры и алгебраические дополнения

Миноры и алгебраические дополнения

Вопросы и ответы