|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема
Структурная теорема
Для формулировки структурной теоремы нам понадобится ввести некоторые новые понятия.
Элемент  назовем регулярным
мономом над
дифференциальным полем
назовем регулярным
мономом над
дифференциальным полем 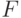 , если
, если  трансцендентен над
трансцендентен над 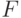 и
является либо логарифмом, либо \vad экспонентой над
и
является либо логарифмом, либо \vad экспонентой над 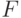 .
Последовательность
элементов
.
Последовательность
элементов 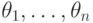 называется последовательностью
регулярных мономов если каждый
ее элемент
называется последовательностью
регулярных мономов если каждый
ее элемент  является регулярным
мономом над
является регулярным
мономом над 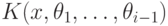 ,
, 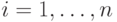 .
.
В структурной теореме нам нужно различать экспоненты и логарифмы, а
именно
через  обозначим множество индексов
обозначим множество индексов  , таких, что
, таких, что  является
экспонентой, а
является
экспонентой, а  - множество индексов
- множество индексов  , таких,
что
, таких,
что 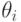 является
логарифмом. Структурная теорема дает необходимое и достаточное условие
трансцендентности очередного элемента последовательности логарифмов и
экспонент.
является
логарифмом. Структурная теорема дает необходимое и достаточное условие
трансцендентности очередного элемента последовательности логарифмов и
экспонент.
24.2. ТЕОРЕМА.
Пусть  - поле констант,
- поле констант, 
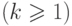 -
последовательность регулярных мономов,
-
последовательность регулярных мономов,  - множество
индексов
- множество
индексов  , таких, что
, таких, что  является экспонентой
является экспонентой  , а
, а  - множество индексов
- множество индексов  , таких, что
, таких, что 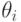 является логарифмом
является логарифмом  .
.
- Пусть
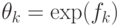 -
экспонента над дифференциальным полем
-
экспонента над дифференциальным полем  ,
,  . Если
элемент
. Если
элемент 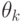 алгебраичен над
алгебраичен над 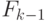 , то
, то 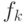 представляется в виде линейной
комбинации с рациональными коэффициентами, где
представляется в виде линейной
комбинации с рациональными коэффициентами, где
 - некоторая константа.
- некоторая константа. - Пусть
 - логарифм над
дифференциальным полем
- логарифм над
дифференциальным полем  ,
,  . Если
элемент
. Если
элемент 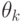 алгебраичен над
алгебраичен над 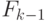 , то
, то 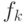 представляется
в виде произведения
рациональных степенейгде
представляется
в виде произведения
рациональных степенейгде
 - некоторая константа.
- некоторая константа.
Заметим, что оба выписанных соотношения выполняются в поле  , которое
является полем рациональных функций над
, которое
является полем рациональных функций над  от
от  независимых переменных.
Освобождаясь от знаменателей и приравнивая коэффициенты при одинаковых
мономах (во 2-м случае нужно предварительно перейти к логарифмической
производной), получим систему линейных уравнений относительно
независимых переменных.
Освобождаясь от знаменателей и приравнивая коэффициенты при одинаковых
мономах (во 2-м случае нужно предварительно перейти к логарифмической
производной), получим систему линейных уравнений относительно  ,
, 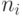 и
и 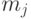 . Если эта система имеет решение в поле констант, такое, что
все
. Если эта система имеет решение в поле констант, такое, что
все  , то
, то 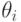 не является регулярным мономом.
не является регулярным мономом.
Применение структурной теоремы проиллюстрируем следующими примерами.
24.3. ПРИМЕР.
Пусть  - поле рациональных чисел, и предположим, что
- поле рациональных чисел, и предположим, что  , где
, где  и
и  - регулярные мономы над
- регулярные мономы над 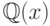 . Используя структурную
теорему легко
видеть, что ни одна из следующих функций:
. Используя структурную
теорему легко
видеть, что ни одна из следующих функций:  ,
, 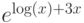 ,
, 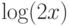 ,
, 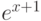 не является регулярным мономом над
не является регулярным мономом над  .
.
24.4. ПРИМЕР. Рассмотрим выражение

Будем строить последовательность расширений полей, начинающуюся с
поля
рациональных чисел  , и содержащую последовательно
вычисляемые части
выписанного выражения.
, и содержащую последовательно
вычисляемые части
выписанного выражения.
Положим  . Элемент
. Элемент 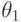 является регулярным мономом,
если не существует константы
является регулярным мономом,
если не существует константы  такой, что
такой, что  . Выполнение этого
условия очевидно, значит
. Выполнение этого
условия очевидно, значит  - регулярный
моном над
- регулярный
моном над  .
.
Положим  . Если
. Если 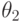 не является регулярным
мономом, то существует константа
не является регулярным
мономом, то существует константа  и рациональное число
и рациональное число  такие, что
такие, что  . Сравнивая степени
. Сравнивая степени  в
левой и правой части,
получаем, что такое соотношение не выполняется ни при каких
в
левой и правой части,
получаем, что такое соотношение не выполняется ни при каких  и
и  ,
следовательно,
,
следовательно, 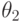 - регулярный моном над
- регулярный моном над 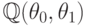 .
.
Положим 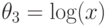 . Структурная теорема дает
нам уравнение
. Структурная теорема дает
нам уравнение  , которое имеет решение
, которое имеет решение  . Заметим, что существование единственного решения у этого
уравнения не
означает, что
. Заметим, что существование единственного решения у этого
уравнения не
означает, что  единственным образом выражается через
единственным образом выражается через 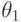 и
и  ; действительно,
; действительно,  ,
где константа
,
где константа 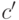 определена только по модулю
определена только по модулю  . В этом случае структурная
теорема может
только подсказать, как переформулировать исходную задачу: исходное выражение
целесообразно переписать в виде
. В этом случае структурная
теорема может
только подсказать, как переформулировать исходную задачу: исходное выражение
целесообразно переписать в виде

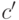 не фигурирует.
не фигурирует.Положим 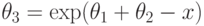 . Структурная
теорема дает нам
условие
. Структурная
теорема дает нам
условие


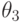 является регулярным мономом. В поле
является регулярным мономом. В поле  исходное выражение принимает вид
исходное выражение принимает вид  .
.Заметим, что исходным выражением последовательность элементов  определяется неоднозначно. В частности, можно при рассмотрении того же
выражения полагать
определяется неоднозначно. В частности, можно при рассмотрении того же
выражения полагать 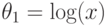 ,
,  ,
,  и
и  . Можно
показать, что в
этом случае
. Можно
показать, что в
этом случае 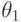 ,
,  ,
, 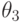 - регулярные мономы, а
- регулярные мономы, а 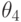 - нет.
- нет.
Прежде, чем переходить к подробному изложению алгоритма Риша, рассмотрим еще один
