|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Базисы Гребнера
Базисы Гребнера в полиномиальных, дифференциальных и разностных модулях
Пусть  - конечная система
элементов. Через
- конечная система
элементов. Через  обозначим свободную
коммутативную полугруппу с единицей (записываемую
мультипликативно),
порожденную элементами множества
обозначим свободную
коммутативную полугруппу с единицей (записываемую
мультипликативно),
порожденную элементами множества  . Элементы этой группы
будем называть мономами. Пусть
. Элементы этой группы
будем называть мономами. Пусть  ,
,  . Порядком монома
. Порядком монома  будем называть сумму
будем называть сумму 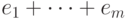 и обозначать ее будем
и обозначать ее будем  .
Предположим, что мономы линейно упорядочены так, что для любого элемента
.
Предположим, что мономы линейно упорядочены так, что для любого элемента  выполняются следующие условия:
выполняются следующие условия:
 |
( 9.1) |
 , то
, то |
( 9.2) |
Тогда будем говорить, что на множестве мономов  задан ранжир.
Следующие примеры показывают, что для одного и того же конечного множества
задан ранжир.
Следующие примеры показывают, что для одного и того же конечного множества  существуют различные ранжиры.
существуют различные ранжиры.
9.1. ПРИМЕР (лексикографическое упорядочение мономов)
Пусть  .
Тогда
.
Тогда  , если либо
, если либо  , либо
, либо  для
для 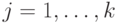 и
и  для некоторого
для некоторого 
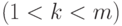 .
.
9.2. ПРИМЕР (стандартный ранжир)
предположим, что  ,
если либо
,
если либо  , либо
, либо  и
и  относительно лексикографического упорядочения.
относительно лексикографического упорядочения.
9.3. ПРИМЕР (упорядочение по полной степени, затем обратное лексикографическое)
Пусть  ,
,  . Положим
. Положим  , если либо
, если либо  , либо
, либо 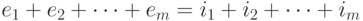 и
существует
и
существует  ,
,  , такое, что
, такое, что  для
для  и
и  .
.
Пусть  - поле и
- поле и  - векторное
- векторное  -пространство с базисом
-пространство с базисом  .
Определим на
.
Определим на  функцию "выделение лидера" следующим
образом: каждый элемент
функцию "выделение лидера" следующим
образом: каждый элемент 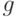 из
из  может быть представлен в виде суммы
может быть представлен в виде суммы  , где лишь конечное
число
коэффициентов
, где лишь конечное
число
коэффициентов  отлично от нуля (такое представление
определено однозначно с
точностью до порядка слагаемых). Среди всех мономов, входящих в это разложение
с ненулевым коэффициентом, выберем максимальный относительно порядка,
введенного на множестве мономов
отлично от нуля (такое представление
определено однозначно с
точностью до порядка слагаемых). Среди всех мономов, входящих в это разложение
с ненулевым коэффициентом, выберем максимальный относительно порядка,
введенного на множестве мономов  . Этот моном будем называть лидером элемента
. Этот моном будем называть лидером элемента  и обозначать через
и обозначать через  . Корректность
такого определения следует из
однозначности разложения элемента векторного пространства по базису и из
линейной упорядоченности множества
. Корректность
такого определения следует из
однозначности разложения элемента векторного пространства по базису и из
линейной упорядоченности множества  .
.
9.4. ОПРЕДЕЛЕНИЕ.
Пусть задан ранжир на множестве мономов  и
и  -
векторное
-
векторное  -пространство с базисом
-пространство с базисом  . Предположим
далее, что
. Предположим
далее, что  является
является  -алгеброй, и
-алгеброй, и  для всех
для всех  . Кроме того, предположим, что
. Кроме того, предположим, что 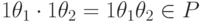 для любых
для любых 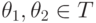 ; в частности, образующие
; в частности, образующие  коммутируют между собой. Такое кольцо будем
называть кольцом обобщенных
многочленов от переменных
коммутируют между собой. Такое кольцо будем
называть кольцом обобщенных
многочленов от переменных  .
.
9.5. ПРИМЕР(кольцо коммутативных многочленов над полем)
Рассмотрим любой ранжир на множестве  . В
качестве
. В
качестве  возьмем алгебру многочленов
возьмем алгебру многочленов ![K[x_1,\dots,x_m]](/sites/default/files/tex_cache/8bdccec6181661e5bb49e34613c082c9.png) от
коммутирующих переменных
от
коммутирующих переменных  над полем
над полем  .
Нетрудно
увидеть, что условие
.
Нетрудно
увидеть, что условие  будет выполнено для
всех
будет выполнено для
всех  , а, следовательно, мы можем рассматривать
, а, следовательно, мы можем рассматривать ![K[x_1,\dots,x_m]](/sites/default/files/tex_cache/8bdccec6181661e5bb49e34613c082c9.png) как кольцо обобщенных многочленов от переменных
как кольцо обобщенных многочленов от переменных  .
.
9.6. ПРИМЕР(кольцо дифференциальных операторов над
полем) Пусть  -
дифференциальное поле с базисным множеством
-
дифференциальное поле с базисным множеством  попарно коммутирующих
между собой дифференцирований. Ранжир на множестве
попарно коммутирующих
между собой дифференцирований. Ранжир на множестве  так же, как
и в примере 9.5, может быть любым. Тогда
кольцо
так же, как
и в примере 9.5, может быть любым. Тогда
кольцо ![D=K[d_1,\dots,d_m]](/sites/default/files/tex_cache/4e47b1452950eef5e67115a73330050d.png) линейных дифференциальных операторов
над
линейных дифференциальных операторов
над  (см. определение 3.4) будет являться кольцом обобщенных многочленов от неизвестных
(см. определение 3.4) будет являться кольцом обобщенных многочленов от неизвестных  .
.
9.7. ПРИМЕР(кольцо дифференциальных операторов над кольцом
многочленов)
Пусть  - дифференциальное поле с базисным множеством
дифференцирований
- дифференциальное поле с базисным множеством
дифференцирований  ,
и пусть
,
и пусть  - кольцо коммутативных многочленов от переменных
- кольцо коммутативных многочленов от переменных  над полем
над полем  .
Определим дифференцирования
.
Определим дифференцирования  кольца
кольца  следующим образом: если
следующим образом: если  , то
, то  для всех
для всех 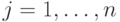 . Выберем теперь для
каждого
. Выберем теперь для
каждого  число
число  и положим
и положим  для
всех
для
всех 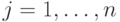 и
и 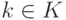 . Тогда кольцо
. Тогда кольцо  линейных
линейных 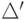 -операторов над кольцом
-операторов над кольцом  будет являться
кольцом обобщенных многочленов от переменных
будет являться
кольцом обобщенных многочленов от переменных 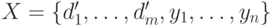 . Действительно, если мы
рассмотрим такой ранжир, что
. Действительно, если мы
рассмотрим такой ранжир, что 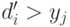 для всех
для всех  ,
, 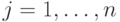 , то, как легко доказать,
условие
, то, как легко доказать,
условие  будет выполнено.
будет выполнено.
9.8. ПРИМЕР(кольцо разностных операторов над полем)
Пусть  - разностное
поле с базисным множеством попарно коммутирующих автоморфизмов
- разностное
поле с базисным множеством попарно коммутирующих автоморфизмов  . Тогда
кольцо
. Тогда
кольцо ![R=K[\alpha_1,\dots,\alpha_m]](/sites/default/files/tex_cache/7854addfe9e7cf7edc7bf52f39dc7155.png) линейных разностных
операторов (см. определение 3.9)
будет являться
кольцом обобщенных многочленов от переменных
линейных разностных
операторов (см. определение 3.9)
будет являться
кольцом обобщенных многочленов от переменных  . В качестве ранжира можно
выбрать любое упорядочение, удовлетворяющее условиям
(9.1)-(9.2).
. В качестве ранжира можно
выбрать любое упорядочение, удовлетворяющее условиям
(9.1)-(9.2).
9.9. ПРИМЕР(кольцо дифференциально-разностных операторов над
полем)
Обобщением примеров 9.6 и 9.8 является случай кольца ![R=K[d_1,\dots,d_m,\alpha_1,\dots,\alpha_q]](/sites/default/files/tex_cache/db75b5e9efa24b9b9db0b3f5e2802085.png) ,
когда часть переменных соответствует дифференцированиям, а другая часть
- автоморфизмам.
,
когда часть переменных соответствует дифференцированиям, а другая часть
- автоморфизмам.
Пусть теперь  - кольцо обобщенных многочленов от
переменных
- кольцо обобщенных многочленов от
переменных  над полем
над полем  , и
, и  - свободный
- свободный  -модуль с
базисом
-модуль с
базисом  . Как векторное пространство над
. Как векторное пространство над  модуль
модуль  имеет в качестве базиса прямое
произведение
имеет в качестве базиса прямое
произведение  множеств
множеств  и
и  .
Это множество мы будем называть множеством термов
модуля
.
Это множество мы будем называть множеством термов
модуля  ,
,  .
Термы перемножать нельзя, однако определено произведение терма на моном
из
соответствующего кольца многочленов. В дальнейшем мы будем обычно
отождествлять терм
.
Термы перемножать нельзя, однако определено произведение терма на моном
из
соответствующего кольца многочленов. В дальнейшем мы будем обычно
отождествлять терм  с вектором
с вектором  .
.
9.10. ОПРЕДЕЛЕНИЕ. Ранжиром на
множестве термов 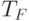 будем называть отношение полного
порядка на
будем называть отношение полного
порядка на 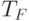 , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
-
 для любого терма
для любого терма 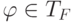 и любого монома
и любого монома  ;
; - если
 , где
, где  , то
, то  для всех
для всех  .
.
