НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 3: Численное решение систем линейных алгебраических уравнений

Проведем несколько равносильных преобразований. Умножим обе части системы на один и тот же скалярный множитель 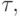$\tau,$ затем прибавим к правой и левой частям системы вектор $\mathbf{u}.$ Систему уравнений можно теперь записать в виде, удобном для итераций:

$\mathbf{u}= \mathbf{Bu}+ \mathbf{F},$

( 2.15)

где $\mathbf{B} = \mathbf{E} - \tau \mathbf{A},\quad \mathbf{F} = \tau \mathbf{f}.$

Теперь построим последовательность приближений к решению системы. Выберем произвольный вектор ${\mathbf{u}}_0$ — начальное приближение к решению. Чаще всего его просто полагают нулевым вектором. Скорее всего, начальное приближение не удовлетворяет (2.15) и, следовательно, исходной системе. При подстановке его в исходное уравнение возникает невязка ${\mathbf{r}}_0 = \mathbf{f} - \mathbf{A}{\mathbf{u}}_0.$ Вычислив невязку, с помощью (2.15) можно уточнить приближение к решению, считая, что

${\mathbf{u}}_1 ={\mathbf{u}}_0 + \tau{\mathbf{r}}_0.$

По первому приближению снова вычисляется невязка, процесс продолжается. В ходе итерации получаем ${\mathbf{u}}_{k + 1} = {\mathbf{u}}_k + \tau{\mathbf{r}}_k, {\mathbf{r}}_k = \mathbf{f} - {\mathbf{Au}}_k.$ Эквивалентная формулировка метода, называемого методом простых итераций, заключается в следующем. Решение (2.15) находится как предел последовательности $\{{\mathbf{u}}_0, {\mathbf{u}}_1, {\mathbf{u}}_2, \ldots\}$ приближений, члены которой связаны рекуррентным соотношением (оно эквивалентно приведенному выше, из записи исключен вектор невязки):

${\mathbf{u}}_{{k + 1}} = {\mathbf{Bu}}_k + {\mathbf{F}},$

( 2.16)

${\mathbf{u}}_0 = 0$ (или любому произвольному вектору). Если предел такой последовательности существует, то говорят о сходимости итерационного процесса к решению СЛАУ.

Существуют другие формы записи метода итераций, например

${\mathbf{u}}_{k + 1} = ({\mathbf{E}} - \tau\mathbf{A}){\mathbf{u}}_k + \tau\mathbf{f}.$

( 2.17)

Канонической формой записи двухслойного итерационного процесса называется следующая:

${\mathbf{D}}_{k + 1}\frac{{\mathbf{u}}_{k + 1} - {\mathbf{u}}_k}{\tau_{k + 1}} + {\mathbf{Au}}_k = \mathbf{f}.$

( 2.18)

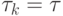При ${\mathbf{D}}_k = {\mathbf{E}}$ , $\tau _{k} = \tau$ последняя формула соответствует однопараметрическому итерационному процессу — рассмотренному выше методу простых итераций. При ${\mathbf{D}}_k = \mathbf{E}$ , $\tau_k= \left\{{\tau_k, k= 1, \ldots , n}\right\}$ — n -шаговому явному итерационному процессу, при ${\mathbf{D}}_k = \mathbf{D^{\prime}}$ , $\tau _{k} = 1$ — методу простой итерации без итерационного параметра. В случае, когда $\mathbf{D} \ne \mathbf{E}$ , итерационный метод называется неявным — для вычисления следующего приближения к решению придется решать (как правило, более простую, чем исходную) систему линейных уравнений.

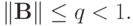
Теорема (достаточное условие сходимости метода простой итерации ). Итерационный процесс (2.16) сходится к решению $\mathbf{U}$ СЛАУ $\mathbf{Au} = \mathbf{F}$ со скоростью геометрической прогрессии при выполнении условия: $\|{\mathbf{B}}\| \le q < 1.$

Доказательство.

Пусть $\mathbf{U}$ — точное решение системы (2). Вычитая из (2.16)-(2.15), получим ${\mathbf{u}}_k - {\mathbf{U}} = \mathbf{B}({\mathbf{u}}_{k - 1} - \mathbf{U})$ , или, обозначив погрешность ${\mathbf{\varepsilon }}_k = {\mathbf{u}}_k - {\mathbf{U}}$ , получим для эволюции погрешности уравнение ${\mathbf{\varepsilon}}_k = {\mathbf{B\varepsilon}}_{k - 1}.$ Справедлива цепочка неравенств: $\|{{\mathbf{u}}_k - {\mathbf{U}}}\| = \|{{\mathbf{\varepsilon}}_k}\| \le \|{\mathbf{B}}\| \cdot \|{{\mathbf{\varepsilon}}_{k - 1}}\| \le q\|{{\mathbf{\varepsilon}}_{k - 1}}\| \le \ldots \le q^k\|{{\mathbf{\varepsilon}}_0}\| = q^k\|{{\mathbf{u}}_0 - {\mathbf{U}}}\|$ , где $0 < q \le \|{\mathbf{B}}\|.$

Отсюда следует, что при $q < 1 \lim\limits_{k \to \infty}{\mathbf{u}}_k = \mathbf{U}.$

Из неравенства $\|{{\mathbf{\varepsilon}}_k}\| \le q^k\|{{\mathbf{\varepsilon}}_0}\|$ можно получить оценку количества итераций,необходимых для достижения точности $\varepsilon,$ т.е. для выполнения условия $\|{{\mathbf{u}}_k - \mathbf{U}}\| = \|{{\mathbf{\varepsilon}}_k}\| \le \varepsilon.$ Эта оценка имеет вид

$$ k \ge \left({\ln{\frac{\mathbf{\varepsilon}}{\|{{\mathbf{\varepsilon}}_0}\|}}}\right)/\ln{q} $.$

Теорема (критерий сходимости метода простой итерации (без доказательства)). Пусть СЛАУ (2.15) имеет единственное решение. Тогда для сходимости итерационного процесса (2.16) необходимо и достаточно, чтобы все собственные значения матрицы ${\mathbf{B}$ по абсолютной величине были меньше единицы.

Сравним по количеству арифметических действий прямые и итерационные методы. Метод Гаусса без выбора главного элемента при $n \gg 1$ требует

$\approx (\frac{2}{3}n^3)$

арифметических действий; метод простой итерации (2.16) $\approx (2n^2 \cdot I)$ , где i — число приближений, необходимое для достижения заданной точности. Значит, при I < n/3 метод итераций становится предпочтительнее. В реальных задачах, в основном, $I \ll n.$ Кроме того, итерационные методы можно делать более эффективными, изменяя итерационные параметры. В ряде случаев итерационные методы оказываются более устойчивыми по отношению к накоплению ошибок округления, чем прямые.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение систем линейных алгебраических уравнений

2.5. Итерационные методы решения СЛАУ

2.5.1. Метод простой итерации

Вопросы и ответы