Блоки

Теорема 3. Два различных блока одного графа могут иметь не более одной общей вершины. Вершина принадлежит более чем одному блоку тогда и только тогда, когда она является шарниром графа.

Доказательство. Пусть и - различные блоки графа . Рассмотрим подграф . Он не является блоком, следовательно, или несвязен, или имеет шарнир. Если несвязен, то и - его компоненты связности и, следовательно, не имеют общих вершин. Если же связен и - шарнир в , то после удаления вершины граф распадается на компоненты связности. При этом все вершины подграфа , отличные от , принадлежат одной компоненте, иначе была бы шарниром в . То же верно для вершин подграфа . Значит, имеется всего две компоненты, одна из которых состоит полностью из вершин графа , другая - из вершин графа . Следовательно, - единственная общая вершина и .

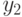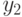Если вершина принадлежит более чем одному блоку, то она инцидентна двум ребрам, и , принадлежащим разным блокам, то есть не являющимся циклически связанными. Но тогда всякий путь, соединяющий и , проходит через , следовательно, - шарнир. Обратно, если - шарнир, то найдутся две смежные с вершины и , принадлежащие разным компонентам связности графа, получаемого удалением вершины . Но тогда ребра и не являются циклически связанными, следовательно, принадлежат разным блокам.