|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Начальные понятия теории графов
Начальные понятия теории графов
Графы являются существенным элементом математических моделей в самых разнообразных областях науки и практики. Они помогают наглядно представить взаимоотношения между объектами или событиями в сложных системах. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.
Цель этой и двух следующих лекций - дать краткое введение в теорию графов. В них приводится минимум понятий, необходимый для того, чтобы можно было начать какую-либо содержательную работу с графами или приступить к более глубокому изучению теории графов. Доказательства приводятся только в тех случаях, когда их сложность не превышает некоторого интуитивно ощущаемого порога. Поэтому, например, такие важные факты, как теорема Кирхгофа или теорема Понтрягина-Куратовского, сообщаются без доказательств.
Определение графа
Для описания строения различных систем, состоящих из связанных между собой элементов, часто используют графические схемы, изображая элементы точками (кружками, прямоугольниками и т.д.), а связи между ними - линиями или стрелками, соединяющими элементы. При этом получаются диаграммы вроде тех, что показаны на рис. 1.1.
На таких диаграммах часто ни способ изображения элементов, ни форма или
длина линий не имеют значения - важно лишь, какие именно пары элементов
соединены линиями. Если посмотреть внимательно, то можно заметить, что
рисунки 1.1а и 1.1 б изображают одну и ту же структуру связей между
элементами  ,
,  ,
,  ,
,  ,
,  ,
,  . Эту же структуру можно описать,
не прибегая к графическому изображению, а просто перечислив пары связанных
между собой элементов:
. Эту же структуру можно описать,
не прибегая к графическому изображению, а просто перечислив пары связанных
между собой элементов:  ,
,  ,
,  ,
, 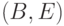 ,
,  ,
, 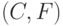 ,
,  . Таким образом, когда мы отвлекаемся от
всех
несущественных подробностей, у нас остаются два списка: список элементов
и список пар элементов. Вместе они составляют то, что математики называют
графом. Из этого примера видно, что понятие графа само по себе не связано
напрямую с геометрией или графикой. Тем не менее, возможность нарисовать
граф - одна из привлекательных черт этого математического объекта.
. Таким образом, когда мы отвлекаемся от
всех
несущественных подробностей, у нас остаются два списка: список элементов
и список пар элементов. Вместе они составляют то, что математики называют
графом. Из этого примера видно, что понятие графа само по себе не связано
напрямую с геометрией или графикой. Тем не менее, возможность нарисовать
граф - одна из привлекательных черт этого математического объекта.
Термин "граф" неоднозначен, это легко заметить, сравнивая приводимые в разных книгах определения. Однако во всех этих определениях есть кое-что общее. В любом случае граф состоит из двух множеств - множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет. Вершины и ребра называются элементами графа. Здесь будут рассматриваться только конечные графы, то есть такие, у которых оба множества конечны. Чтобы получить законченное определение графа того или иного типа, необходимо уточнить еще три момента.
-
Ориентированный или неориентированный?
Прежде всего, нужно договориться, считаем ли мы пары
 и
и  различными. Если да, то говорят, что
рассматриваются упорядоченные пары (порядок элементов в паре важен), если
нет - неупорядоченные. Если ребро
различными. Если да, то говорят, что
рассматриваются упорядоченные пары (порядок элементов в паре важен), если
нет - неупорядоченные. Если ребро  соединяет вершину
соединяет вершину  с вершиной
с вершиной  и пара
и пара  считается
упорядоченной, то это ребро называется ориентированным, вершина
считается
упорядоченной, то это ребро называется ориентированным, вершина  - его началом, вершина
- его началом, вершина  - концом. Если же эта пара
считается неупорядоченной, то ребро называется неориентированным,
а обе вершины - его концами. Чаще всего рассматривают графы,
в которых все ребра имеют один тип - либо ориентированные, либо неориентированные.
Соответственно и весь граф называют ориентированным или неориентированным.
На рисунках ориентацию ребра (направление от начала к концу) указывают
стрелкой. На рис. 1.1 показаны неориентированные графы, а на рис. 1.2 - ориентированные.
- концом. Если же эта пара
считается неупорядоченной, то ребро называется неориентированным,
а обе вершины - его концами. Чаще всего рассматривают графы,
в которых все ребра имеют один тип - либо ориентированные, либо неориентированные.
Соответственно и весь граф называют ориентированным или неориентированным.
На рисунках ориентацию ребра (направление от начала к концу) указывают
стрелкой. На рис. 1.1 показаны неориентированные графы, а на рис. 1.2 - ориентированные. -
Следующий пункт, требующий уточнения, - могут ли разные ребра иметь одинаковые начала и концы? Если да, то говорят, что в графе допускаются кратные ребра. Граф с кратными ребрами называют также мультиграфом. На рис. 1.2 изображены два графа, левый является ориентированным мультиграфом, а правый - ориентированным графом без кратных ребер.
-
Петли.
Ребро, которому поставлена в соответствие пара вида
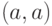 ,
то есть ребро, соединяющее вершину
,
то есть ребро, соединяющее вершину  с
нею же самой, называется петлей.
Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.
с
нею же самой, называется петлей.
Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.
Комбинируя эти три признака, можно получить разные варианты определения понятия графа. Особенно часто встречаются неориентированные графы без петель и кратных ребер. Такие графы называют обыкновенными. Если в графе нет кратных ребер, то можно просто отождествить ребра с соответствующими парами вершин - считать, что ребро это и есть пара вершин. Чтобы исключить петли, достаточно оговорить, что вершины, образующие ребро, должны быть различны. Это приводит к следующему определению обыкновенного графа.
Определение. Обыкновенным графом
называется пара 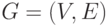 , где
, где 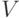 - конечное
множество,
- конечное
множество,  -
множество неупорядоченных пар различных элементов из
-
множество неупорядоченных пар различных элементов из 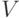 . Элементы
множества
. Элементы
множества 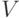 называются вершинами графа, элементы
множества
называются вершинами графа, элементы
множества  - его ребрами.
- его ребрами.
Слегка модифицируя это определение, можно получить определения других типов графов без кратных ребер: если заменить слово "неупорядоченных" словом "упорядоченных", получится определение ориентированного графа без петель, если убрать слово "различных", получится определение графа с петлями. Ориентированный граф часто называют орграфом.
В дальнейшем термин "граф" мы будем употреблять в смысле "обыкновенный граф", а рассматривая другие типы графов, будем специально это оговаривать.
Множество вершин графа  будем обозначать через
будем обозначать через 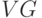 , множество
ребер -
, множество
ребер - 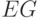 , число вершин -
, число вершин - 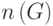 , число
ребер -
, число
ребер - 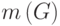 .
.
Из определения видно, что для задания обыкновенного графа достаточно
перечислить его вершины и ребра, причем каждое ребро должно быть парой
вершин. Положим, например,  ,
, 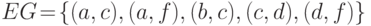 .
Тем самым задан граф
.
Тем самым задан граф  с
с  ,
, 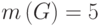 .
Если граф не слишком велик, то более наглядно представить его можно
с помощью рисунка, на котором вершины изображаются кружками или иными
значками, а ребра - линиями, соединяющими вершины. Заданный выше
граф
.
Если граф не слишком велик, то более наглядно представить его можно
с помощью рисунка, на котором вершины изображаются кружками или иными
значками, а ребра - линиями, соединяющими вершины. Заданный выше
граф  показан на рисунке 1.3.
Мы будем часто пользоваться именно этим способом
представления графа, при этом обозначения вершин иногда будут помещаться
внутри кружков, изображающих вершины, иногда рядом с ними, а иногда, когда
имена вершин несущественны, и вовсе опускаться.
показан на рисунке 1.3.
Мы будем часто пользоваться именно этим способом
представления графа, при этом обозначения вершин иногда будут помещаться
внутри кружков, изображающих вершины, иногда рядом с ними, а иногда, когда
имена вершин несущественны, и вовсе опускаться.



