|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Машины Тьюринга
Вычислимость и разрешимость
Упорядоченный набор из  слов в алфавите
слов в алфавите  называется
называется  -местным
набором над
-местным
набором над  . Множество всех
. Множество всех  -местных наборов
над
-местных наборов
над  обозначим через
обозначим через 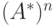 .
Любое подмножество
.
Любое подмножество  множества
множества 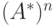 называется
называется  -местным словарным отношением.
-местным словарным отношением.
Любое, возможно частичное, отображение  называется
называется  -местной словарной функцией. Область определения
функции
-местной словарной функцией. Область определения
функции  обозначается через
обозначается через  .
.
Результатом работы программы  на входном
псевдослове
на входном
псевдослове  называется псевдослово
называется псевдослово  , которое появляется на ленте
в момент остановки программы; если программа работает бесконечно, то
результат не определен.
, которое появляется на ленте
в момент остановки программы; если программа работает бесконечно, то
результат не определен.
Программу, которая в процессе работы над любым псевдословом  не сдвигает головку левее пробела, расположенного слева от
не сдвигает головку левее пробела, расположенного слева от  -го слова
псевдослова
-го слова
псевдослова  , будем называть
, будем называть  -программой.
-программой.
Словарное  -местное отношение
-местное отношение  называется полуразрешимым, если
существует
называется полуразрешимым, если
существует  -программа
-программа  , которая
останавливается в точности на всех псевдословах, имеющих вид
, которая
останавливается в точности на всех псевдословах, имеющих вид

 .
.Словарное  -местное отношение
-местное отношение  называется разрешимым,
если
называется разрешимым,
если  и
и 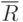 полуразрешимы (под
полуразрешимы (под 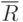 здесь понимается множество
здесь понимается множество  .
.
Словарная  -местная функция
-местная функция  называется вычислимой по
Тьюрингу, если существует программа
называется вычислимой по
Тьюрингу, если существует программа  такая, что
такая, что

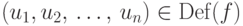 и
и 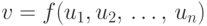 ,
в противном случае результат не определен.
,
в противном случае результат не определен.Вычислимые по Тьюрингу функции уместно было бы назвать полувычислимыми, а полувычислимые с разрешимой областью определения — вычислимыми, но это противоречит установившимся традициям.
Вычисление числовых функций
Чтобы вычислять значения числовых функций с помощью тьюринговых программ,
необходимо выбрать способ кодирования на ленте аргументов и значений
функции. Мы рассматриваем функции из  в
в  ,
где
,
где  — множество натуральных чисел,
включая
— множество натуральных чисел,
включая  , а
, а  .
.
Значения функции и ее аргументов будем записывать в бинарном, унарном или
каком-либо ином коде, для чего нам потребуется, соответственно, алфавит 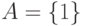 ,
,  и т.д. Значения аргументов
перед вычислением должны быть представлены на ленте в виде псевдослова
и т.д. Значения аргументов
перед вычислением должны быть представлены на ленте в виде псевдослова
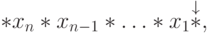
 — код
— код  -го аргумента
-го аргумента  .
.После вычисления содержимое ленты должно иметь вид

 — код значения функции при заданных значениях
аргумента.
— код значения функции при заданных значениях
аргумента.Упражнения
- Составить программу, перерабатывающую
псевдослово
 в псевдослово
в псевдослово 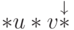 ,
где
,
где  — бинарный, а
— бинарный, а 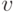 — унарный код
некоторого числа из
— унарный код
некоторого числа из  .
. - Составить программу сложения и умножения чисел в унарном и бинарном кодах.
- Составить программу для удвоения числа в бинарном и унарном кодах.
- Составить программу деления нацело натуральных чисел в унарном коде.
