|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Машины Тьюринга
Начальное математическое обеспечение
Приведем несколько программ, для которых введем обозначения, и в дальнейшем будем использовать их для построения более сложных программ. Они будут составлять начальное математическое обеспечение программирования.
В таблице приведены их схемы в предположении, что алфавит  состоит из символов
состоит из символов  ; а символ
; а символ  обозначен через
обозначен через  .
.
Кроме того, считаем, что  и
и  —
произвольные псевдослова над
алфавитом
—
произвольные псевдослова над
алфавитом  ;
;  ,
,  —
слова в алфавите
—
слова в алфавите  ;
;  — произвольный символ
из
— произвольный символ
из  ;
;  — слово, полученное из
слова
— слово, полученное из
слова  путем изменения
порядка символов на противоположный;
путем изменения
порядка символов на противоположный;  .
.
Программы  и
и  , описанные в начале таблицы,
используются в последующих программах.
, описанные в начале таблицы,
используются в последующих программах.
Сдвиг головки влево до ближайшего пробела.Обозначение 
Сдвиг головки вправо до ближайшего пробела.Обозначение 
Копирование  -го слова.Обозначение
-го слова.Обозначение 
Удаление буквы со сдвигом. Обозначение 
Циклический сдвиг  слов. Обозначение
слов. Обозначение 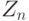
Удаление  -го слова. Обозначение
-го слова. Обозначение 
Методика доказательства правильности программ
Рассматриваемая методика предназначена для доказательства правильности алгоритмов, представленных в виде графов, вершинам которых поставлены в соответствие операторы над памятью, а дугам — переходы от оператора к оператору. Одну из вершин назовем входной, ей соответствует оператор, с которого начинается выполнение алгоритма, а выходных вершин может быть несколько. Считаем, что входная и выходная вершины помечены, соответственно, входящей и выходящей стрелками. Такие представления алгоритмов называют блок-схемами. Доказать правильность алгоритма — это значит доказать следующее утверждение:
- Если входные данные удовлетворяют входному условию, то алгоритм через конечное число шагов завершает работу и выходные данные удовлетворяют требуемому выходному условию.
На практике такое утверждение часто разбивают на два.
- Если входные данные удовлетворяют входному условию и алгоритм через конечное число шагов завершает работу, то выходные данные удовлетворяют требуемому выходному условию.
- Если входные данные удовлетворяют входному условию, то алгоритм через конечное число шагов завершает работу.
Алгоритм, для которого доказано утверждение 1, называется частично правильным или частично корректным. Если же доказаны утверждения 1 и 2, то алгоритм называется правильным или корректным.
Заметим, что когда доказательство утверждения 2 представляет непреодолимые трудности, то ограничиваются доказательством утверждения 1. Таковы, например, итерационные алгоритмы, для которых неизвестна область сходимости. В таком случае, если алгоритм в приемлемое время завершает свою работу, то правильность ответа гарантируется.
Остановимся на доказательстве частичной корректности. Методика заключается в следующем:
- Для контроля над ходом вычислений выбираются так называемые контрольные дуги. К числу контрольных обязательно относят входную и все выходные дуги, а также некоторое количество других дуг, так, чтобы в граф-схеме алгоритма оказались "разрезанными" все циклы.
- Для каждой контрольной дуги формулируется индуктивное условие, которому предположительно должно удовлетворять содержимое памяти алгоритма при каждом его прохождении через рассматриваемую дугу. Считаем, что все контрольные дуги (в дальнейшем будем называть их контрольными точками) и соответствующие им индуктивные утверждения пронумерованы.
- Для каждой пары
 ,
,  контрольных точек, для
которых в блок-схеме имеется путь из
контрольных точек, для
которых в блок-схеме имеется путь из  в
в  , минующий другие
контрольные точки, выбираются все такие пути, и для каждого выбранного пути
доказывается утверждение (индуктивный шаг): "Если при очередном проходе
через точку
, минующий другие
контрольные точки, выбираются все такие пути, и для каждого выбранного пути
доказывается утверждение (индуктивный шаг): "Если при очередном проходе
через точку  выполнялось индуктивное
предположение
выполнялось индуктивное
предположение 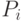 и если реализуется рассматриваемый путь,
то при достижении точки
и если реализуется рассматриваемый путь,
то при достижении точки  будет выполняться условие
будет выполняться условие  ".
".
Если все индуктивные шаги доказаны, то, используя принцип математической индукции, можно утверждать частичную корректность алгоритма. Для доказательства полной корректности остается доказать завершаемость программы через конечное число шагов.


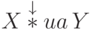






![L^n,\ r,[\cup_i\ (\t{если}\
a_i)
[\ast,\ R^{n+1},\ a_i,\ L^{n+1}, a_i, r]]\ (\t{до}\ \ast),\ R^n](/sites/default/files/tex_cache/091cbf3cc1d4164f09479ddd839d11b5.png)


![[r, \cup_i\ (\t{если}\ a_i)
[l,\ a_i],\ r]\ (\t{до}\ \ast)](/sites/default/files/tex_cache/15bc57c3b9a04ff63e1211bcd273ee21.png)


![R,\ [L^{n+1},\ r, \cup_i\
(\t{если}\ a_i)[S^n, a_i]](\t{до}\ \ast)](/sites/default/files/tex_cache/7c7e733f1edf15a48ff6fe69f5602442.png)


![Z_n,\ [\ast, l]\ (\t{до}\
\ast)](/sites/default/files/tex_cache/334c60b26b5b640c07fb40d04fbf4f22.png)