| Россия, Новосибирск |
Выразимость в арифметике
Элиминация кванторов: элиминация кванторов
При всей простоте метод доказательства невыразимости с помощью автоморфизмов страдает очевидным недостатком: очень часто требуемого автоморфизма нет. Например, натуральные числа с операцией прибавления единицы вообще не допускают никакого нетривиального автоморфизма. (Тем не менее там выразимо очень немногое, как мы вскоре увидим.) Целые числа с операцией прибавления единицы допускают автоморфизмы (сдвиги), но эти автоморфизмы не позволяют доказать, что отношение порядка невыразимо (поскольку оно устойчиво относительно сдвигов).
Более прямой метод доказательства состоит в том, что мы
предъявляем некоторый класс 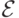 предикатов, который содержит все
выразимые предикаты и не содержит интересующего нас предиката.
При этом мы доказываем, что
предикатов, который содержит все
выразимые предикаты и не содержит интересующего нас предиката.
При этом мы доказываем, что 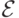 содержит все выразимые
предикаты, таким способом: проверяем, что
содержит все выразимые
предикаты, таким способом: проверяем, что 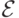 содержит все предикаты,
выразимые атомарными формулами, а также замкнут относительно
логических операций (объединение, пересечение, дополнение) и
операции проекции (соответствующей навешиванию квантора
существования; квантор всеобщности выражается через квантор
существования). Часто класс
содержит все предикаты,
выразимые атомарными формулами, а также замкнут относительно
логических операций (объединение, пересечение, дополнение) и
операции проекции (соответствующей навешиванию квантора
существования; квантор всеобщности выражается через квантор
существования). Часто класс 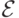 совпадает с классом всех
предикатов, выразимых бескванторными формулами (иногда надо
расширить сигнатуру), и потому этот метод называют методом
"элиминации кванторов". (Это краткое описание, возможно, станет
яснее из приводимых далее примеров.)
совпадает с классом всех
предикатов, выразимых бескванторными формулами (иногда надо
расширить сигнатуру), и потому этот метод называют методом
"элиминации кванторов". (Это краткое описание, возможно, станет
яснее из приводимых далее примеров.)
Начнем с такого примера.
Пусть сигнатура содержит равенство,
одноместную функцию  (прибавление единицы) и константу
(прибавление единицы) и константу  . Носителем интерпретации будет множество
. Носителем интерпретации будет множество 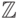 целых чисел,
символы сигнатуры интерпретируются естественным образом.
В этой ситуации изоморфизмов не существует, так что предыдущий
способ доказательства невыразимости здесь неприменим.
целых чисел,
символы сигнатуры интерпретируются естественным образом.
В этой ситуации изоморфизмов не существует, так что предыдущий
способ доказательства невыразимости здесь неприменим.
Тем не менее класс выразимых предикатов весьма ограничен: это предикаты, выразимые бескванторными формулами. Будем называть две формулы (рассматриваемой нами сигнатуры) эквивалентными (в данной интерпретации), если они выражают один и тот же предикат, то есть истинны при одних и тех же значениях переменных.
Теорема 28. Для всякой формулы рассматриваемой нами сигнатуры существует эквивалентная ей бескванторная формула.
Будем доказывать индукцией по построению (или, если угодно, по
длине) формулы  существование эквивалентной ей в
существование эквивалентной ей в  бескванторной формулы. Для удобства (чтобы рассматривать один
случай, а не два) будем считать, что наша формула может
содержать только кванторы существования, но не всеобщности. Это
законно, так как формулы
бескванторной формулы. Для удобства (чтобы рассматривать один
случай, а не два) будем считать, что наша формула может
содержать только кванторы существования, но не всеобщности. Это
законно, так как формулы  и
и  эквивалентны.
эквивалентны.
Случай, когда  есть атомарная формула, очевиден — она и
так бескванторная. Если
есть атомарная формула, очевиден — она и
так бескванторная. Если  является конъюнкцией, дизъюнкцией
или импликацией двух частей, достаточно заменить каждую часть
на эквивалентную бескванторную (что можно сделать по предположению индукции).
является конъюнкцией, дизъюнкцией
или импликацией двух частей, достаточно заменить каждую часть
на эквивалентную бескванторную (что можно сделать по предположению индукции).
Единственный содержательный случай — когда формула  начинается с квантора существования, то есть имеет вид
начинается с квантора существования, то есть имеет вид 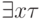 (пусть под квантором стоит переменная
(пусть под квантором стоит переменная  ).
Мы рассуждаем по индукции, поэтому можем считать,
что формула
).
Мы рассуждаем по индукции, поэтому можем считать,
что формула 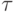 — бескванторная.
Она имеет (возможно) и другие параметры, скажем,
— бескванторная.
Она имеет (возможно) и другие параметры, скажем,  . Чтобы подчеркнуть это, обычно
вместо
. Чтобы подчеркнуть это, обычно
вместо 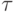 пишут
пишут 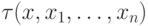 . Нам надо найти бескванторную
формулу нашей сигнатуры, эквивалентную формуле
. Нам надо найти бескванторную
формулу нашей сигнатуры, эквивалентную формуле

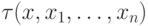 представляет собой булеву
комбинацию атомарных формул. Посмотрим на те атомарные формулы,
которые содержат переменную
представляет собой булеву
комбинацию атомарных формул. Посмотрим на те атомарные формулы,
которые содержат переменную  . Атомарная формула представляет
собой равенство двух термов
. Атомарная формула представляет
собой равенство двух термов  ; здесь
; здесь  и
и 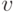 — либо переменные, либо константа
— либо переменные, либо константа  . Если
переменная
. Если
переменная  входит и в левую, и в правую часть, то (в этой интерпретации)
такая атомарная формула либо всегда истинна, либо всегда ложна,
и ее можно заменить на какую-нибудь тождественно истинную или
тождественно ложную формулу, не содержащую
входит и в левую, и в правую часть, то (в этой интерпретации)
такая атомарная формула либо всегда истинна, либо всегда ложна,
и ее можно заменить на какую-нибудь тождественно истинную или
тождественно ложную формулу, не содержащую  . После этого останутся
атомарные формулы, которые можно записать как
. После этого останутся
атомарные формулы, которые можно записать как
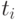 — либо целая константа, либо выражение вида
— либо целая константа, либо выражение вида  , где
, где 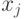 — какая-то другая переменная, а
— какая-то другая переменная, а  — целое
число. Мы позволили себе слегка отступить от канонов, разрешив прибавлять
и вычитать целые константы вместо того, чтобы применять функцию
— целое
число. Мы позволили себе слегка отступить от канонов, разрешив прибавлять
и вычитать целые константы вместо того, чтобы применять функцию  в левой и правой частях равенства. Ясно, что это не меняет класса
выразимых формул, зато позволяет оставить
в левой и правой частях равенства. Ясно, что это не меняет класса
выразимых формул, зато позволяет оставить  в левой части, а
константу перенести в правую.
в левой части, а
константу перенести в правую.Теперь сравним формулу


 .
Формула
.
Формула  представляет собой дизъюнкцию формул,
полученных в результате подстановки различных
представляет собой дизъюнкцию формул,
полученных в результате подстановки различных 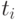 вместо
вместо  в
бескванторную формулу
в
бескванторную формулу 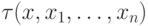 . (После
подстановки можно вернуться к обычному виду записи формулы,
заменив прибавление констант на нужное количество применений
функции
. (После
подстановки можно вернуться к обычному виду записи формулы,
заменив прибавление констант на нужное количество применений
функции  с той или другой стороны равенства.)
с той или другой стороны равенства.)Очевидно, что если для каких-то значений переменных  формула
формула  истинна, то для этих значений
истинна, то для этих значений  истинна и формула
истинна и формула  . В самом деле, если истинен
. В самом деле, если истинен  -й член дизъюнкции, то в формуле
-й член дизъюнкции, то в формуле  в
качестве
в
качестве  можно взять значение выражения
можно взять значение выражения 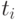 .
.
Верно ли обратное? Не обязательно. Вполне возможно, что тот  ,
который существует и делает формулу
,
который существует и делает формулу  истинной,
отличается от всех
истинной,
отличается от всех 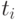 . Но мы пропустили по существу только
один случай — все такие
. Но мы пропустили по существу только
один случай — все такие  в некотором смысле одинаковы, так
как они делают все атомарные формулы, содержащие
в некотором смысле одинаковы, так
как они делают все атомарные формулы, содержащие  , ложными,
поэтому все равно, какой из таких
, ложными,
поэтому все равно, какой из таких  выбрать. Отметим также,
что хотя бы один такой
выбрать. Отметим также,
что хотя бы один такой  найдется, поскольку
найдется, поскольку 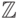 бесконечно, а выражений
бесконечно, а выражений 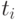 лишь конечное число.
лишь конечное число.
Обозначим через  формулу, которая получится
из
формулу, которая получится
из 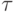 заменой всех атомарных формул, содержащих
заменой всех атомарных формул, содержащих  , на тождественно
ложные формулы. Сказанное выше объясняет, почему формула
, на тождественно
ложные формулы. Сказанное выше объясняет, почему формула  эквивалентна дизъюнкции
эквивалентна дизъюнкции 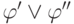 . Мы достигли цели
— нашли бескванторную формулу, эквивалентную формуле
. Мы достигли цели
— нашли бескванторную формулу, эквивалентную формуле  .
.
Легко понять, что отношение порядка  не выражается
бескванторной формулой нашей сигнатуры, поскольку такая формула
может включать лишь атомарные формулы вида
не выражается
бескванторной формулой нашей сигнатуры, поскольку такая формула
может включать лишь атомарные формулы вида  и для нее
случай, когда
и для нее
случай, когда  сильно больше
сильно больше  , неотличим от
случая, когда
, неотличим от
случая, когда  сильно меньше
сильно меньше  . Тем самым мы доказали (чего
нельзя было сделать методом автоморфизмов), что отношение
. Тем самым мы доказали (чего
нельзя было сделать методом автоморфизмов), что отношение  невыразимо
(в данной интерпретации данной сигнатуры).
невыразимо
(в данной интерпретации данной сигнатуры).
Немного более сложное рассуждение понадобится, если добавить к сигнатуре отношение порядка.

