Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

Лекция 2: Численное решение дифференциальных уравнений в частных производных параболического типа на примере уравнения теплопроводности

A
|
версия для печати
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

2.4. Исследование сходимости разностных схем для многомерного уравнения теплопроводности

Простейшая явная разностная схема для численного решения двумерного уравнения теплопроводности

$ \frac{{\partial}u}{{\partial}t} = \frac{{{\partial}^2 u}}{{{\partial}x^2}} + \frac{{{\partial}^2 u}}{{{\partial}y^2}} $

получается путем замены производных конечными разностями

$ \frac{{u_{ml}^{n + 1} - u_{ml}^{n}}}{\tau} = \frac{{u_{m - 1, l}^{n} - 2u_{ml}^{n} + u_{m + 1, l}^{n}}}{{h_x^2}} + \frac{{u_{{m, l} - 1}^{n} - 2u_{ml}^{n} + u_{{m, l} + 1}^{n}}}{{h_y^2}} $

или, в операторной форме,

$ \frac{{u_{ml}^{n + 1} - u_{ml}^{n}}}{\tau} = {\mathbf{\Lambda}}_1 u_{ml}^{n} + {\mathbf{\Lambda}}_2 u_{ml}^{n}. $

Исследование спектральной устойчивости этой схемы ( u_{me}^{n} = {\lambda}^{n} e^{i{\alpha} m + i{\beta}l}, {\alpha} ,{\beta}\in \left[{0, 2 {\pi}}\right] ) приводит к следующему результату для спектра оператора послойного перехода:

$ {\lambda}(\alpha ,{\beta},{\tau}, h_x , h_y ) = 1 - 4 \frac{\tau}{h_x^2} {\sin}^2 \frac{\alpha }{2} - 4 \frac{\tau}{{h_y^2}} {\sin}^2 \frac{\beta}{2}, $

откуда получаем условие устойчивости

${\tau} \le \frac{1}{2(h_x^{- 2} + h_y^{- 2} )}. $

Для неявной схемы

$ \frac{{u_{ml}^{n + 1} - u_{ml}^{n}}}{\tau} = {{\Lambda}}_1 u_{ml}^{n + 1} + {{\Lambda}}_2 u_{ml}^{n + 1} $

исследование на устойчивость по спектральному признаку дает

{\lambda} = \frac{1}{{1 + 4 \frac{\tau}{{h_x^2}} {\sin}^2 \frac{\alpha }{2} + 4 \frac{\tau}{{h_y^2}} {\sin}^2 \frac{\beta }{2}}},

т.е. схема устойчива при любых 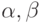{\alpha},{\beta}.

Приведем исследование спектральной устойчивости для схемы переменных направлений.

Рассмотрим переход с нижнего на верхний временный слой. В таком случае можно положить u_{ml}^{n} = e^{i{\alpha} m + i{\beta}l} ; сомножитель \lambda ^{n} опускаем, так как рассматривается один переход с n - го на (n + 1) - й слой в предположении, что известно решение на n - ом слое (можно было бы написать, u_{ml}^{n} = {Ce}^{i{\alpha} m + i{\beta}l}, где C = \lambda ^{n}, но в этом нет смысла, так как C в дальнейших выкладках сократится).

Тогда на первом этапе получим $ \tilde {u}_{ml} = \lambda_1 u_{ml}^{n} $, а на втором — u_{ml}^{n + 1} = \lambda_2 \tilde {u}_{ml} = (\lambda_1 \lambda_2 )u_{ml}^{n}.

Вычисление \lambda _{1} и \lambda _{2} дает

\lambda_1 = \frac{{1 - 4 \frac{\tau}{h_x^2} {\sin}^2 \frac{\alpha }{2}}}{{1 + 4 \frac{\tau}{h_y^2} {\sin}^2 \frac{\alpha }{2}}}, \lambda_2 = \frac{{1 - 4 \frac{\tau}{h_x^2} {\sin}^2 \frac{\beta }{2}}}{{1 + 4 \frac{\tau}{{h_y^2}} {\sin}^2 \frac{\beta }{2}}}.

Окончательно спектр оператора послойного перехода представим в виде произведения спектров на каждом промежуточном этапе.

{\lambda}(\alpha ,{\beta},{\tau}, h_x , h_y ) = \lambda_1 \lambda_2 = \frac{{(1 - 4 \frac{\tau}{{h_x^2}} {\sin}^2 \frac{\alpha }{2})(1 - 4 \frac{\tau}{{h_x^2}} {\sin}^2 \frac{\beta }{2})}}{{(1 + 4 \frac{\tau}{{h_y^2}} {\sin}^2 \frac{\alpha }{2})(1 + 4 \frac{\tau}{{h_y^2}} {\sin}^2 \frac{\beta }{2})}}.

Схема безусловно устойчива.

Исследование схемы расщепления на аппроксимацию проведем на примере локально - одномерной схемы для двумерного уравнения теплопроводности

$ \frac{{\tilde {u}_{ml} - u_{ml}^{n}}}{\tau} = {{{\Lambda}}}_1 \tilde {u}_{ml}, \quad \frac{{u_{ml}^{n + 1} - \tilde {u}_{ml}}}{\tau} = {{{\Lambda}}}_2 u_{ml}^{n + 1} . $

Запишем эти уравнения в операторной форме

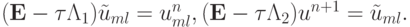
({\mathbf{E}} -{\tau}{{\Lambda}}_1 ) \tilde {u}_{ml} = u_{ml}^{n}, ({\mathbf{E}} -{\tau}{{{\Lambda}}}_2 )u^{n + 1} = \tilde {u}_{ml}.

Подействуем на обе части второго уравнения оператором ({\mathbf{E}} -{\tau}{\mathbf{\Lambda}}_1):

({\mathbf{E}} -{\tau}{{\Lambda}}_1 )({\mathbf{E}} -{\tau}{{{\Lambda}}}_2)u_{ml}^{n + 1} = ({\mathbf{E}} -{\tau}{{{\Lambda}}}_1 ) \tilde{u}_{ml}.

Так как

({\mathbf{E}} -{\tau}{{\Lambda}}_1 ) \tilde {u}_{ml} = u_{ml}^{n}, \quad \mbox{то} \quad ({\mathbf{E}} - {\tau}{{{\Lambda}}}_1 )({\mathbf{E}} -{\tau}{{{\Lambda}}}_2 )u_{ml}^{n + 1} = u_{ml}^{n}.

Это уравнение приводится к виду

$ \frac{{u_{ml}^{n + 1} - u_{ml}^{n}}}{\tau} = {{{\Lambda}}}_1 u_{ml}^{n + 1} + {{{\Lambda}}}_2 u_{ml}^{n + 1} - {\tau}^2 {{{\Lambda}}}_1 {{{\Lambda}}}_2 u_{ml}^{n + 1}. $

Последнее слагаемое в правой части является величиной порядка O(\tau ) и определяет погрешность аппроксимации.

Если правая часть f(t, x, y) не нулевая, то схему можно переписать, например

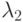$ \frac{{\tilde {u}_{ml} - u_{ml}^{n}}}{\tau} = {{{\Lambda}}}_1 \tilde {u}_{ml} + \frac{1}{2}f_{ml}^{n}, \frac{{u_{ml}^{n + 1} - u_{ml}^{n}}}{\tau} = {{{\Lambda}}}_2 u_{ml}^{n + 1} + \frac{1}{2} \tilde{f}_{ml} . $
Дальше >>
< Лекция 1 || Лекция 2: 12345678 || Лекция 3 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 29
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу