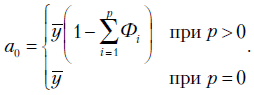|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Стационарные временные ряды, модели авторегрессии - скользящего среднего
10.8. Алгоритм выбора модели оптимальной сложности для временного ряда в АРСС(p, q)-моделях
Все множество наблюдений  разбивают на две выборки:
разбивают на две выборки:
- обучающую с объемом наблюдений
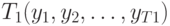 ;
; - экзаменационную
 с объемом наблюдений
с объемом наблюдений .
.
На обучающей выборке определяют числовые характеристики временного ряда, а именно: среднее, дисперсию, автоковариации и автокорреляционные функции (АКФ):
Организуются циклы по переменным  - числу параметров авторегрессии и
- числу параметров авторегрессии и  - числу параметров скользящего среднего:
- числу параметров скользящего среднего:
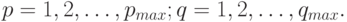
Для каждой пары ( ) вычисляются оценки параметров авторегрессии
) вычисляются оценки параметров авторегрессии ) путем решения системы р линейных уравнений
) путем решения системы р линейных уравнений

По известным автоковариациям  вычисляется модифицированная последовательность ковариаций
вычисляется модифицированная последовательность ковариаций  :
:
Вычисляются начальные значения  , т.е. формируется начальный вектор \
, т.е. формируется начальный вектор \ .
.
Далее используется алгоритм Ньютона - Рафсона вида

При этом

и начальный вектор определен выше.
Если  , для некоторого выбираемого заранее малого
, для некоторого выбираемого заранее малого  , то итерационный процесс завершается.
, то итерационный процесс завершается.
Оценки 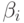 параметров скользящего среднего находятся по формулам
параметров скользящего среднего находятся по формулам

где  получен в результате применения алгоритма Ньютона - Рафсона (см. выше).
получен в результате применения алгоритма Ньютона - Рафсона (см. выше).
Вычисляем свободный член модели
Определяем оценку дисперсии белого шума:
Вычисляем остаточные ошибки модели на обучающей выборке. Пусть 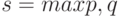 , тогда остаточные ошибки на обучающей выборке
, тогда остаточные ошибки на обучающей выборке  имеют вид
имеют вид
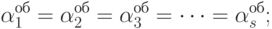
Найдем остаточные ошибки модели на проверочной последовательности. Полагаем:
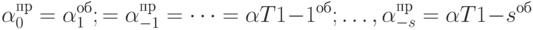
и далее
Вычисляем на экзаменационной (проверочной) последовательности среднюю сумму квадратов ошибок:
Оформляем конец циклов на  и
и  .
.
Выбираем пару  и
и  , для которой
, для которой  принимает минимальное значение:
принимает минимальное значение:

Далее производится оценка коэффициентов авторегрессии и скользящего среднего для модели выбранной оптимальной сложности с 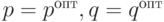 , повторяя описанный выше алгоритм для всей выборки
, повторяя описанный выше алгоритм для всей выборки и получая окончательные значения коэффициентов
и получая окончательные значения коэффициентов .
.
Экономичность модели. Помимо "внешнего" критерия при построении модели можно использовать принцип экономичности. Включение дополнительных переменных в модель увеличивает адекватность модели (на обучающей выборке), так как средняя ошибка модели убывает. Часто можно заменить одну модель другой - более экономичной. Например, СС( )-модель
)-модель

эквивалентна модели  , что легко проверить.
, что легко проверить.
Для того чтобы сделать модель более экономичной, считают, что коэффициенты авторегрессии и скользящего среднего должны иметь  -статистики больше или равны 2 (чтобы каждый коэффициент значимо отличался от нуля при 5%-ном уровне значимости). Кроме того, необходимо следить за тем, чтобы коэффициенты не были сильно коррелированны друг с другом. Сильная корреляция коэффициентов делает модель неустойчивой. В этом случае следует исключать те коэффициенты, которые в наименьшей степени ухудшают результаты прогноза.
-статистики больше или равны 2 (чтобы каждый коэффициент значимо отличался от нуля при 5%-ном уровне значимости). Кроме того, необходимо следить за тем, чтобы коэффициенты не были сильно коррелированны друг с другом. Сильная корреляция коэффициентов делает модель неустойчивой. В этом случае следует исключать те коэффициенты, которые в наименьшей степени ухудшают результаты прогноза.
Кроме того, важно, чтобы остатки оцениваемой модели были сериально некоррелированные. Наличие сериальной корреляции остатков сигнализирует о систематических изменениях в последовательности 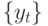 , которые не могут быть учтены АРСС-моделью.
, которые не могут быть учтены АРСС-моделью.
Чтобы проверить корреляцию остатков, строят АКФ и ЧАКФ для остатков оцениваемой модели. Затем можно использовать  -статистики Бокса - Пирса и Льюиса - Бокса (см. (10.49)-(10.50)). Они позволяют определить, будут ли автокорреляции остатков или частные автокорреляции статистически значимы. Обычно можно предполагать наличие сериальной корреляции остатков при превышении критического уровня
-статистики Бокса - Пирса и Льюиса - Бокса (см. (10.49)-(10.50)). Они позволяют определить, будут ли автокорреляции остатков или частные автокорреляции статистически значимы. Обычно можно предполагать наличие сериальной корреляции остатков при превышении критического уровня  -статистикой при 10%-ном уровне значимости. В этом случае велика вероятность построения другой модели, лучше отражающей специфику процесса.
-статистикой при 10%-ном уровне значимости. В этом случае велика вероятность построения другой модели, лучше отражающей специфику процесса.
Стационарность и обратимость модели. Из теории вероятностей известно, что выборочные АКФ и ЧАКФ аппроксимируют АКФ и ЧАКФ реального временного ряда в том случае, если предполагать стационарность ряда  . Далее,
. Далее,  и
и  -статистики также предполагают стационарность ряда
-статистики также предполагают стационарность ряда  .
.
Если искомый ряд  не стационарный, то первым шагом в подходе Бокса - Дженкинса является взятие первой, второй и следующих разностей временного ряда
не стационарный, то первым шагом в подходе Бокса - Дженкинса является взятие первой, второй и следующих разностей временного ряда

и так далее до тех пор, пока в результате не получится стационарный временной ряд. Этот подход обладает серьезным недостатком, так как не позволяет включать в модель долговременные составляющие. Современные подходы к построению модели временных рядов в условиях нестационарности рассмотрены в последующих главах книги.
Подход Бокса - Дженкинса требует также обратимости модели. Она означает возможность представления модели в виде конечного или бесконечного, но сходящегося авторегрессионного процесса. Это необходимо для АКФ и ЧАКФ. Рассмотрим, к примеру, СС(1)-модель
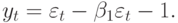
Если  , то
, то
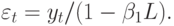
Разлагая в ряд правую часть равенства, получаем:

Полученная модель представляет собой сходящуюся авторегрессионную модель бесконечного порядка, для которой могут быть посчитаны АКФ и ЧАКФ. Однако если 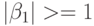 , то последовательность
, то последовательность 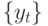 не может быть представлена сходящейся авторегрессией. В общем случае для АРСС(
не может быть представлена сходящейся авторегрессией. В общем случае для АРСС( )-модели корни многочлена
)-модели корни многочлена  должны лежать вне единичного круга. Тогда модель обратима.
должны лежать вне единичного круга. Тогда модель обратима.
Заметим, что могут существовать и необратимые модели с "долгосрочной памятью", которые нельзя построить по методу Бокса - Дженкинса. Например, модель стационарного процесса

с постоянным средним  , дисперсией и автоковариациями
, дисперсией и автоковариациями  и \
и \ . Записывая модель в эквивалентном виде
. Записывая модель в эквивалентном виде
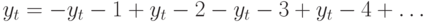
убеждаемся, что ЧАКФ не затухают с увеличением лага 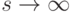 .
.






 , а вектор
, а вектор с координатами
с координатами .
.
 .
.