НОУ ИНТУИТ | Введение в эконометрику. Лекция 10: Стационарные временные ряды, модели авторегрессии

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 10.09.2016 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

10.6. Построение АРСС-моделей

Первым шагом в подборе АРСС-модели наблюдаемого временного ряда является оценка среднего - $\mu$ , дисперсии - $(\sigma _{y})^{2}$ и автокорреляций $\rho _{k}$ . В предположении стационарности и эргодичности (возможности получения оценок по одной реализации процесса) применимы следующие оценки:

(10.44)

(10.45)

и

(10.46)

Выборочные АКФ из (10.46) и ЧАКФ, полученные по формулам (10.39)-(10.43), сравнивают с различными теоретическими функциями, чтобы идентифицировать процесс, породивший данную выборочную реализацию.

Дж. Бокс и Г. Дженкинс (1976) получили формулу для расчета дисперсии выборочной АКФ $r_{s}$ в предположении, что $y_{t}$ - стационарны с нормально распределенными ошибками. Тогда

$D(r_{s}) = T-1 для s = 1,$

(10.47)

для

(10.48)

при настоящем значении $r_{s} = 0$ . Более того, в большой выборке ( - велико) $r_{s}$ нормально распределено с нулевым средним. Для коэффициентов ЧАКФ АР(р)-модели доказано, что $D(Ф_{p+ i, p+i}) \approx Т^{-1}$ .

На практике полученные выборочные значения АКФ и ЧАКФ тестируются на значимость с использованием (10.47) и (10.48). Например, для 95%-ого доверительного интервала (двух стандартных отклонений), если $r_{1}$ превышает $2Т^{-1/2}$ , то следует отвергнуть нулевую гипотезу о том, что АКФ первого порядка статистически незначимо отличается от нуля. Это означает, что q > 0 , где - показатель числа запаздываний в модели SS(q) . Затем, пусть $s = 2, D(r_{2}) = (1 + 2r_{1}^{2}) / T$ .

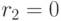Если, например, $r_{1} = 0,5 и Т = 100$ , то $D(r_{2}) = 0,015$ и $\sigma (r_{2}) \approx 0,123$ . Тогда если вычисленное по выборке значение $r_{2}$ превышает $2 \times (0,123)$ (два стандартных отклонения), то при принятых ограничениях с 95%-ной вероятностью можно утверждать, что гипотезу $r_{2} = 0$ надо отвергнуть. Следовательно, q > 1 . Повторяя процесс проверки гипотез для различных можно пытаться идентифицировать порядок процесса.

Однако если просматривать большое число АКФ, то можно обнаружить, что некоторые АКФ превышают $2\sigma (r_{s})$ , хотя настоящие $\rho _{s} = 0$ . Это вызвано как 5%-ными ошибками первого рода, так и несоответствием реальных распределений теоретическим предпосылкам нормальности ошибок.

Следующая -статистика может быть использована для тестирования, когда группа АКФ значимо отличается от нуля. -статистика Бокса - Пирса имеет вид

(10.49)

Если данные порождены стационарным АРСС-процессом, то асимптотически $x^{2}$ -распределенная с степенями свободы. Интуитивно понятно, что большие значения АКФ ведут к большим значениям . Если выборочное превышает соответствующее табличное значение , то отвергается гипотеза о незначимости группы АКФ. Отметим, что альтернативная гипотеза означает, что хотя бы одна АКФ не равна нулю.

Однако оказалось, что даже в средней величины выборках -статистика работает плохо. Для малых выборок используют модифицированную -статистику Льюиса - Бокса, вычисленную по формуле

(10.50)

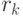Если выборочное значение -статистики превышает критическое значение $x^{2}$ -распределения с степенями свободы, то по крайней мере одно значение $r_{k}$ статистически отлично от нуля при данном уровне значимости. Особо полезны эти статистики для проверки гипотезы об образовании остатками вычисленной АРСС( p, q )-модели белого шума. Поэтому если рассчитывать АКФ для остатков оцененной АРСС( p, q )-модели, то число степеней свободы уменьшается на число коэффициентов модели. Следовательно, используя остатки для АРСС( p, q )-модели, необходимо проверять с помощью $x^{2}$ -распределения с s - p - q степенями свободы. Если включена свободная постоянная, то используем таблицы $x^{2}$ -распределения с s - p - q - 1 степенями свободы.

10.7. Селекция моделей АРСС

Наиболее простой и популярный в настоящее время метод селекции моделей предполагает построение множества моделей с различными и , а затем выбор модели, минимизирующей выбранный критерий селекции, который характеризует качество модели.

Существующие "внутренние" критерии селекции выражают компромисс между сложностью модели и величиной суммы квадратов остатков. Так, наиболее популярными являются информационный критерий Акайке (AIC) и бестестовый критерий Шварца (SBC), вычисляемые по формулам

$AIC = T ln(R^{2}) + 2n,\\ SBC = T ln(R^{2}) + n ln(T),$

где

	-	число используемых наблюдений;
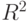$R^{2}$	-	сумма квадратов остатков (ошибок) модели;
	-	число оцениваемых параметров модели.

Так как ln(T) > 2 , то оптимальная модель SBC будет менее сложной, чем оптимальная модель AIC. Стоимость "добавки" лишнего слагаемого больше для SBC-критерия, чем для AIC-критерия. Доказано, что с увеличением выборки SBC-модели асимптотически состоятельны, в то время как AIC-модели становятся слишком сложными.

Рассмотренные выше критерии отбора являются "внутренними", т.е. используют данные, уже ранее использованные для построения моделей. Если позволяет величина выборки, то гораздо надежнее использовать "внешние" критерии селекции, т.е. независимые наблюдения, не вошедшие в первоначальную выборку. Алгоритм построения АРСС( p, q )-модели по внешнему критерию минимизации ошибок на "экзаменующей" выборке рассмотрен ниже.

Дальше >>

Введение в эконометрику

Введение в эконометрику

Стационарные временные ряды, модели авторегрессии - скользящего среднего

10.6. Построение АРСС-моделей

10.7. Селекция моделей АРСС

Вопросы и ответы

Студенты

Авторизоваться

Введение в эконометрику

Введение в эконометрику

Стационарные временные ряды, модели авторегрессии - скользящего среднего

10.6. Построение АРСС-моделей

10.7. Селекция моделей АРСС

Вопросы и ответы

Студенты