|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Методологические вопросы прогнозирования временных рядов
5.4. Выделение тренда в случае нестационарного временного ряда
Процесс выделения тренда (выравнивание ряда) включает в себя три этапа:
- выбор типа кривой, соответствующей характеру изменения ряда;
- определение числовых значений параметров кривой;
- оценка качества подобранной модели тренда.
На практике используется несколько приемов, позволяющих подобрать соответствующую (адекватную) действительности форму кривой.
Первый прием - визуальный - является наиболее простым. Форма кривой выбирается на основе графического изображения временного ряда, формы его корреляционного поля. Корреляционным полем временного ряда  называется множество точек
называется множество точек 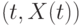 на плоскости
на плоскости 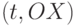 . Однако при этом есть риск субъективного и произвольного выбора. Результат выбора зависит от масштаба графического изображения. Но при относительно простых конфигурациях корреляционного поля и незначительных отклонениях (помехах) от тенденции развития визуальный подход дает вполне приемлемые результаты. Для уменьшения субъективизма следует привлекать по возможности всю информацию об исследуемом процессе, в том числе о внутренней структуре и движущих силах процесса.
. Однако при этом есть риск субъективного и произвольного выбора. Результат выбора зависит от масштаба графического изображения. Но при относительно простых конфигурациях корреляционного поля и незначительных отклонениях (помехах) от тенденции развития визуальный подход дает вполне приемлемые результаты. Для уменьшения субъективизма следует привлекать по возможности всю информацию об исследуемом процессе, в том числе о внутренней структуре и движущих силах процесса.
Второй прием заключается в вычислении последовательных разностей
Порядок разностей, при котором они становятся примерно одинаковыми, берется в качестве степени аппроксимирующего (выравнивающего) многочлена. Так, если малыми оказываются первые разности  , то для выравнивания берется многочлен первой степени
, то для выравнивания берется многочлен первой степени  , если малы разности второго порядка
, если малы разности второго порядка  , то
, то  и т.д.
и т.д.
Ясно, что такой прием не универсален и может использоваться при подборе кривых, описываемых многочленами. Если уравнение кривой путем некоторого преобразования (обычно путем логарифмирования) можно свести к многочлену, то его можно применить и в этом случае. Однако при этом необходимо следить уже не за постоянством величины конечных разностей (5.13), а за их преобразованными значениями.
Например, уравнение гиперболы  можно считать многочленом первой степени от функции
можно считать многочленом первой степени от функции 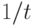 . Кроме того, путем логарифмирования к линейному виду можно преобразовать такие функции, как
. Кроме того, путем логарифмирования к линейному виду можно преобразовать такие функции, как
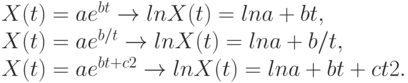
В таблице 5.1 приведены уравнения кривых, их графики, критерии, по которым эти кривые выбираются, а также системы нормальных уравнений метода наименьших квадратов (МНК) для нахождения коэффициентов этих кривых.
Данный подход менее субъективен, так как после визуального выбора кривой с использованием графиков следует проверка ее соответствия временному ряду по критерию выбора кривой (см. табл. 5.1).
Часто используются другие критерии отбора. Обычно в качестве критерия принимают сумму квадратов отклонений фактических значений от расчетных, полученных выравниванием. Выбирается кривая, которой соответствует минимальное значение критерия. Однако минимум суммы квадратов еще не означает, что тенденция развития временного ряда описана наилучшим образом. Это объясняется тем, что через любой набор из  точек на плоскости всегда можно провести многочлен степени
точек на плоскости всегда можно провести многочлен степени 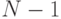 . Поэтому, выбрав достаточно сложную кривую, можно сделать нулевой сумму квадратов отклонений расчетных значений от заданных. Однако в этом случае вряд ли будет отражена тенденция дальнейшего развития процесса.
. Поэтому, выбрав достаточно сложную кривую, можно сделать нулевой сумму квадратов отклонений расчетных значений от заданных. Однако в этом случае вряд ли будет отражена тенденция дальнейшего развития процесса.
Следовательно, отбор кривых следует проводить в два этапа. На первом этапе по большей части данных строят различного вида зависимости  . Затем по оставшимся данным (проверочной последовательности) с помощью критерия минимума квадратов отклонений выбирают кривую с минимальным значением критерия на проверочной последовательности. Этот прием более трудоемкий, чем описанный в табл. 5.1, но, как правило, дает лучшие результаты при прогнозировании тенденции развития временного ряда.
. Затем по оставшимся данным (проверочной последовательности) с помощью критерия минимума квадратов отклонений выбирают кривую с минимальным значением критерия на проверочной последовательности. Этот прием более трудоемкий, чем описанный в табл. 5.1, но, как правило, дает лучшие результаты при прогнозировании тенденции развития временного ряда.
5.5. Автокорреляция остатков
Вычитая из данных  выровненные значения получаем остатки, случайную составляющую тренда
выровненные значения получаем остатки, случайную составляющую тренда
Обычно считается, что выравнивание удовлетворительное, если остатки 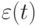 образуют стационарный процесс с нулевым математическим ожиданием
образуют стационарный процесс с нулевым математическим ожиданием ![m\varepsilon (t) = M[\varepsilon (t)] = 0](/sites/default/files/tex_cache/6ee381df231de8e0a907b2ba1518dcd8.png) .
.
Кроме того, для корректного применения МНК необходимо более жесткое предположение, что 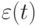 - случайные независимые (хотя бы некоррелированные) величины с
- случайные независимые (хотя бы некоррелированные) величины с  .
.
Если  коррелируют между собой, то в модели присутствует автокорреляция остатков. Метод наименьших квадратов и в этом случае дает несмещенные и состоятельные оценки коэффициентов уравнений кривых. Однако получаемые при этом стандартные ошибки и доверительные интервалы для коэффициентов оказываются заниженными. Это может привести к ошибочным выводам при оценке качества отобранной модели поведения временного ряда. Значительная корреляция остатков сигнализирует о том, что либо кривая подобрана неудачно, либо необходимо строить еще одну модель для описания поведения самих остатков
коррелируют между собой, то в модели присутствует автокорреляция остатков. Метод наименьших квадратов и в этом случае дает несмещенные и состоятельные оценки коэффициентов уравнений кривых. Однако получаемые при этом стандартные ошибки и доверительные интервалы для коэффициентов оказываются заниженными. Это может привести к ошибочным выводам при оценке качества отобранной модели поведения временного ряда. Значительная корреляция остатков сигнализирует о том, что либо кривая подобрана неудачно, либо необходимо строить еще одну модель для описания поведения самих остатков  .
.
Итак, при анализе модели тренда необходимо определить, присутствует ли автокорреляция в  . Предварительную оценку случайности поведения остатков проводят на основе критерия поворотных точек. В соответствии с ним каждое значение
. Предварительную оценку случайности поведения остатков проводят на основе критерия поворотных точек. В соответствии с ним каждое значение  ряда остатков сравнивают с двумя рядом стоящими значениями
ряда остатков сравнивают с двумя рядом стоящими значениями 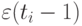 и
и 
Если 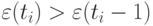 и
и  или
или 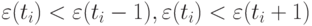 , то точка
, то точка  считается поворотной (в ней достигается локальный максимум или минимум соответственно). Далее подсчитывают общее количество поворотных точек
считается поворотной (в ней достигается локальный максимум или минимум соответственно). Далее подсчитывают общее количество поворотных точек  . В случайном ряду остатков должно выполняться строгое неравенство
. В случайном ряду остатков должно выполняться строгое неравенство
Квадратные скобки здесь означают, что берется целая часть числа (не путать с процедурой округления). Отметим, что критерий поворотных точек сигнализирует только о наличии положительной корреляции в ряде остатков. Если число поворотных точек  велико, приближается к
велико, приближается к  , то можно говорить о наличии отрицательной корреляции между соседними членами временного ряда остатков. Критерий поворотных точек является предварительным, его следует дополнить другими более точными критериями.
, то можно говорить о наличии отрицательной корреляции между соседними членами временного ряда остатков. Критерий поворотных точек является предварительным, его следует дополнить другими более точными критериями.
Простейшим из известных критериев является критерий Неймана. Расчетное значение критерия
Для доказательства положительной корреляции вычисленное значение  должно быть меньше
должно быть меньше  , а для доказательства отрицательной корреляции
, а для доказательства отрицательной корреляции  должно быть больше
должно быть больше  (табл. 5.2).
(табл. 5.2).
Число наблюдений, 
|
Положительная автокорреляция при 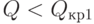
|
Отрицательная автокорреляция при 
|
||
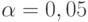 |
 |
 |
 |
|
| 10 | 1,18 | 0,84 | 3,61 | 3,26 |
| 15 | 1,29 | 0,99 | 3,30 | 2,99 |
| 20 | 1,37 | 1,10 | 3,12 | 2,84 |
| 25 | 1,42 | 1,17 | 2,99 | 2,74 |
| 30 | 1,47 | 1,24 | 2,90 | 2,67 |
Помимо критерия Неймана для временных рядов используется хорошо изученный . Он основан практически на той же статистике и отличается множителем
. Он основан практически на той же статистике и отличается множителем 
Этот тест подробно исследован и реализован во всех статистических пакетах (STATGRAPHICS, STATISTICA и др.).
Пусть
Можно показать, что  . Отсюда вывод: чем ближе
. Отсюда вывод: чем ближе  к двум, тем меньше автокорреляция остатков временного ряда. Более того, ученые показали, что существуют две границы
к двум, тем меньше автокорреляция остатков временного ряда. Более того, ученые показали, что существуют две границы  и
и  верхняя,
верхняя, 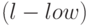 нижняя, которые зависят от
нижняя, которые зависят от  , числа параметров кривой и уровня значимости
, числа параметров кривой и уровня значимости  . Результаты теста Дарбина - Ватсона можно представить в следующем виде (табл. 5.3).
. Результаты теста Дарбина - Ватсона можно представить в следующем виде (табл. 5.3).
Наличие зоны неопределенности, конечно, несколько затрудняет использование теста Дарбина - Ватсона. Ширина зоны неопределенности может быть значительной. Например, при 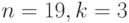 она образует интервал (0,218; 0,463). Поэтому многие дальнейшие исследования были направлены на построение тестов, которые сужают зону неопределенности.
она образует интервал (0,218; 0,463). Поэтому многие дальнейшие исследования были направлены на построение тестов, которые сужают зону неопределенности.
| Значение статистики DW | Вывод |
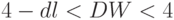 |
Гипотеза о независимости остатков отвергается, есть отрицательная корреляция |
 |
Неопределенность |
 |
Принимается гипотеза о независимости остатков |
 |
Принимается гипотеза о независимости остатков |
 |
Неопределенность |
 |
Гипотеза о независимости остатков отвергается, есть положительная корреляция |



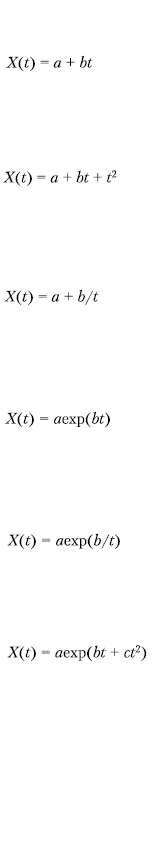

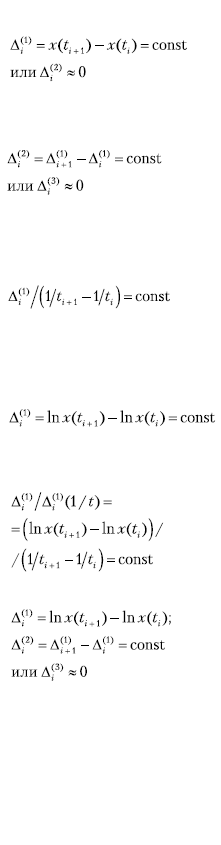


![P > [2(n - 2)/3-2 \sqrt{(16n - 29)}/90)].](/sites/default/files/tex_cache/84abd0d928a1bbebc73f94f320fef70b.png)



