|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Множественная регрессия
3.1. Постановка задачи
Пусть дана система случайных величин  . Для простоты будем считать, что все случайные величины центрированы, т.е.
. Для простоты будем считать, что все случайные величины центрированы, т.е.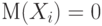 .
.
Рассмотрим случайный вектор
а также матрицу
Математическим ожиданием матрицы, элементами которой являются случайные величины, назовем матрицу, составленную из математических ожиданий элементов исходной матрицы.
Тогда, учитывая, что
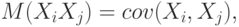
получаем матрицу
Она называется ковариационной матрицей случайного вектора .
.
Если случайные величины 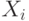 не только центрированы, но и нормированы, т.е. если
не только центрированы, но и нормированы, т.е. если  , то
, то 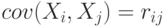 , где
, где 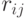 - коэффициенты корреляции для случайных величин
- коэффициенты корреляции для случайных величин  .
.
Ковариационная матрица в этом случае равна
и называется корреляционной матрицей.
Ранее отмечалось, что регрессионный анализ заключается в построении математических зависимостей на основе экспериментальных данных и статистическом анализе результатов.
Рассмотрим линейную модель регрессии, использующую  -факторы,
-факторы,
где
 |
- | номер наблюдения (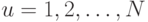 ); ); |
 |
- | вектор-столбец, состоящий из значений  -й переменной в -й переменной в  наблюдениях; наблюдениях; |
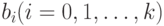 |
- | теоретические значения коэффициентов модели; |
 |
- | ошибка в  -м наблюдении. -м наблюдении. |
Данные в  наблюдениях удобно записывать в табличном виде. Заметим, что
наблюдениях удобно записывать в табличном виде. Заметим, что 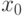 обычно считают фиктивной переменной, тождественно равной единице,
обычно считают фиктивной переменной, тождественно равной единице,  .
.
Таким образом, 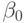 - свободный член в уравнении (3.1), а число реальных переменных, включенных в уравнение (3.1), равно
- свободный член в уравнении (3.1), а число реальных переменных, включенных в уравнение (3.1), равно  .
.
Стандартная процедура регрессионного анализа, выполняемого на основе метода наименьших квадратов, требует выполнения условий Гаусса - Маркова, сформулированных в главе 2.
При этих условиях, в частности, случайные ошибки eu имеют нулевое математическое ожидание, т.е. , не коррелируют друг с другом и имеют одинаковые дисперсии. Другими словами,
, не коррелируют друг с другом и имеют одинаковые дисперсии. Другими словами, , где
, где  , а
, а  - единичная матрица.
- единичная матрица.
Представим матрицу исходных данных в виде таблицы (табл. 3.1).
Таблица 3.1
Обозначим  тогда
тогда  , где
, где 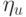 - неслучайная величина. Исходя из этого,
- неслучайная величина. Исходя из этого,
Последнее условие является условием однородности (гомоскедастичности) наблюдений.
В дальнейшем мы используем часть табл. 3.1, а именно матрицу 
которая называется информационной матрицей или матрицей плана эксперимента.
Расчетную модель запишем в виде










