НОУ ИНТУИТ | Теория экспериментов с конечными автоматами. Лекция 20: Диагностическая задача в интервальной постановке

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 17.02.2011 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 3 студентам

| Поделиться |

Поддержать программу

Аннотация: Исследуется диагностическая задача для линейных автоматов, когда наблюдаемая на выходах реакция автоматов представлена в виде интервалов в поле GF(p). Предложены методы решения диагностической задачи с использованием модифицированной конструкции дерева преемников и путем сведения ее к решению систем линейных алгебраических уравнений с интервальной правой частью. Описан генетический алгоритм для решения упомянутой системы, значительно сокращающий время поиска решений.

Ключевые слова: реакция, вектор, координаты, ПО, диагностическая задача , поле, диагностическая задача, множества, автомат, место, ветвь, дерево, информация, матрица, ранг, система линейных уравнений, мощность, размерность, проверка допустимости, вычисление, опыт, генетический алгоритм, генетический алгоритм , мутация, улучшение, хромосомы, целевая функция, работ, операторы, селекция, кодирование, декодирование, бит, длина, определение, поиск, значение, вероятность, вычисления программы, программа, genetic algorithm, Search, optimization, AND, machine learning, компьютер

Постановка задачи и алгебраический метод решения

В классической диагностической задаче для линейных автоматов предполагается, что каждая выходная реакция в момент времени - это вектор $\bar y(t)=[y_1(t), \dots, y_m(t)]'$ , координаты y_i(t) которого представляют собой точные значения. Поскольку практически значения координат наблюдаемой реакции автомата получаются в результате измерений, они неизбежно содержат погрешности, размеры которых зависят от точности измерительных приборов. Поэтому более реальной по сравнению с классической задачей является диагностическая задача , в которой реакция автомата представлена в виде интервалов в поле GF(p) :

$\bar y(t)=[[ \underline y_1(t), \bar y_1(t)], \dots, [\underline y_m(t), \bar y_m(t)]]'$

( 20.1)

Решением интервальной диагностической задачи, заключающейся в определении начального состояния автомата по наблюдаемой его реакции на подаваемую диагностическую последовательность, будем считать такое состояние автомата из множества допустимых начальных состояний, если, стартуя из него, автомат в каждый момент времени порождает выходной вектор, координаты которого принадлежат интервальному вектору (20.1). Заметим, что, как и в случае классической задачи, мы будем считать интервальную диагностическую задачу разрешимой, если искомое начальное состояние определяется однозначно.

Понятно, что чем больше ширина интервалов в выходных векторах, тем сложнее найти начальное состояние автомата. Если же интервалы в выходных векторах полностью покрывают поле GF(p) , то нахождение начальных состояний становится невозможным. Такая ситуация вполне может иметь место при малых значениях , поэтому далее предполагается, что $p \ge 5$ .

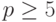Для решения диагностической задачи необходимо иметь ДП, общий метод построения которой в классическом случае описан в [18]. Остановимся кратко на методе построения ДП, ориентированном на решение интервальной диагностической задачи. Построение ДП в этом случае может быть осуществлено с использованием конструкции классического диагностического дерева [18] с внесенными в нее некоторыми незначительными изменениями. Эти изменения касаются способа формирования преемника -группы.

В классическом случае каждое состояние автомата любого сигма-множества -группы имеет единственного преемника в одном и только одном сигма-множестве преемника упомянутой -группы. Отсюда следует, что в классическом случае каждая -группа, связанная с любой ветвью диагностического дерева, содержит в своих сигма-множествах одно и то же суммарное число состояний, равное мощности множества допустимых начальных состояний автомата.

Построение преемника сигма-множества -группы по некоторому входному сигналу в интервальном диагностическом дереве будем осуществлять следующим образом. Сначала вычисляем все состояния-преемники этого сигма-множества по упомянутому входному сигналу и соответствующие "интервальные" реакции автомата. Каждая "интервальная" реакция ЛА заменяется множеством точных реакций, которое представляет собой все возможные комбинации из точных значений, принадлежащих соответствующему интервалу. Таким образом, каждому состоянию-преемнику будет соответствовать некоторое конечное множество точных реакций. Cостояния-преемники будут помещаться в одно и то же сигма-множество, если в соответствующих им множествах точных реакций есть совпадающие между собой. Это правило формирования сигма-множеств -группы следующего уровня может привести к тому, что одно сигма-множество предшествующего уровня в следующем уровне дерева попадает в несколько сигма-множеств. Таким образом, в двух новых сигма-множествах может находиться одно и то же состояние-преемник. Отсюда вытекает, что общее число состояний в преемнике -группы в интервальном диагностическом дереве может оказаться больше мощности множества допустимых начальных состояний автомата.

Что касается правил, по которым некоторая ветвь интервального диагностического дерева становится оконечной, то они остаются теми же, что и в классическом диагностическом дереве. Проиллюстрируем построение интервального диагностического дерева на примере.

Рассмотрим ЛА над полем GF(7) , заданный с помощью следующих характеристических матриц:

$A= \left [ \begin {matrix} 2&1&4\\ 5&2&6\\ 3&0&1 \end {matrix} \right ], B= \left [ \begin {matrix} 3\\ 4\\ 1 \end {matrix} \right ], C= \left [ \begin {matrix} 5&0&3\\ 1&4&6 \end {matrix} \right ], D= \left [ \begin {matrix} 6\\ 1 \end {matrix} \right ]$

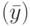Пусть множество допустимых начальных состояний этого ЛА содержит два следующих состояния: [456]' [105]' . Классическое диагностическое дерево для рассматриваемого автомата представлено на рис.20.1. Над каждой -группой на этом рисунке в прямоугольнике помещена информация о состояниях-преемниках $(\bar s)$ и выходных реакциях $(\bar y)$ . Ниже помещены сигма-множества (в фигурных скобках), составляющие -группу. Из этого рисунка следует, что рассматриваемый автомат имеет 7 диагностических последовательностей длины 1: $u=0, u=1, \dots, u=6$ .

Рис. 20.1.

Теперь построим фрагменты интервального диагностического дерева (одну его ветвь для входного сигнала 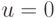u=0 ) в предположении, что при измерении реакции ЛА по каждой координате выходного вектора может произойти ее искажение на одну единицу как в меньшую, так и в большую сторону. Этот фрагмент представлен на рис.20.2.

Рис. 20.2.

При переходах ЛА из состояний [456]', [105]' в состояния [234]', [101]' соответственно вычисляемые точные реакции есть [34]', [63]' . При наличии оговоренных выше погрешностей измерения эти точные реакции превращаются в интервальные реакции [[2,4]', [3,5]]', [[5,0], [2,4]]' . Каждую из этих реакций заменяем соответственно множеством всех возможных комбинаций величин из приведенных интервалов:

$\left \{ \left [ \begin {matrix} 2\\ 3 \end {matrix} \right ], \left [ \begin {matrix} 2\\ 4 \end {matrix} \right ], \left [ \begin {matrix} 2\\ 5 \end {matrix} \right ], \left [ \begin {matrix} 3\\ 3 \end {matrix} \right ], \left [ \begin {matrix} 3\\ 4 \end {matrix} \right ], \left [ \begin {matrix} 3\\ 5 \end {matrix} \right ], \left [ \begin {matrix} 4\\ 3 \end {matrix} \right ], \left [ \begin {matrix} 4\\ 4 \end {matrix} \right ], \left [ \begin {matrix} 4\\ 5 \end {matrix} \right ] \right \} ,\\ \left \{ \left [ \begin {matrix} 5\\ 2 \end {matrix} \right ], \left [ \begin {matrix} 5\\ 3 \end {matrix} \right ], \left [ \begin {matrix} 5\\ 4 \end {matrix} \right ], \left [ \begin {matrix} 6\\ 2 \end {matrix} \right ], \left [ \begin {matrix} 6\\ 3 \end {matrix} \right ], \left [ \begin {matrix} 6\\ 4 \end {matrix} \right ], \left [ \begin {matrix} 0\\ 2 \end {matrix} \right ], \left [ \begin {matrix} 0\\ 3 \end {matrix} \right ], \left [ \begin {matrix} 0\\ 4 \end {matrix} \right ] \right \}$

С использованием этих множеств построим теперь сигма-множества -группы. Так, поскольку реакция [23]' из первого множества не совпадает ни с одной реакцией из второго, то соответствующее ей состояние-преемник [234]' образует простое, т. е. одноэлементное, сигма-множество. Аналогичная ситуация имеет место для всех остальных элементов обоих множеств. Следовательно, преемником множества допустимых начальных состояний является -группа, содержащая 18 одноэлементных сигма-множеств, среди которых по 9 штук содержит одно и то же состояние.

Вернемся теперь к интервальной диагностической задаче. Для нахождения неизвестного начального состояния $\bar s(0)=[s_1(0), \dots, s_n(0)]'$ по известной ДП $\bar u(0), \bar u(1), \dots, \bar u(k)$ и наблюдаемой в процессе проведения эксперимента с ЛА выходной последовательности $\bar y(0), \bar y(1), \dots, \bar y(k)$ , сформируем следующую СЛАУ:

$\begin {cases} C\bars(0)=\bar y(0)-D\bar u(0),\\ CA\bar s(0)=\bar y(1)-CB \bar u(0)-D\bar u(1),\\ ………………………………………………….\\ CA^k\bar s(0)=\bar y(k)-CA^{k-1}B\bar u(0)- \dots -CB\bar u(k-1)-D\bar u(k) \end {cases}$

( 20.2)

Эта система получена на основе формулы полной реакции ЛА для 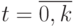$t=\overline {0,k}$ .

Поскольку выходные реакции $\bar y(0), \bar y(1)m \dots, \bar y(k)$ представляют собой интервальные вектора, то правые части системы (20.2) также являются интервальными векторами, тогда как матрица системы (20.2) является точной.

В общем случае число уравнений в системе (20.2), которое обозначим через $\nu$ , может не совпадать с числом неизвестных, равным размерности ЛА. Если $\nu < n,$ то, как известно из алгебры, общее решение такой системы представляется с использованием свободных переменных и матрица системы приводится к квадратной. Если $\nu >n$ , то из факта существования у ЛА диагностической последовательности вытекает существование решения системы (20.2). Последнее означает, что ее ранг равен n и поэтому матрица системы и в этом случае может быть приведена к квадратной.

Исходя из сказанного, решение рассматриваемой интервальной диагностической задачи в математическом плане сводится к решению СЛАУ с точной квадратной матрицей и интервальной правой частью.

Представим такую систему в общем виде:

( 20.3)

где $A=|a_{ij}|_{n \times n}$ - матрица, элементами которой являются элементы поля $GF(p), B=[B_1, \dots, B_n]'$ , а каждое B_i является интервалом или мультиинтервалом (объединением нескольких интервалов).

Тривиальный способ нахождения всех решений системы (20.3) состоит в замене ее интервальной правой части всевозможными конкретными значениями из соответствующих интервалов и поиска решений получающихся при этом обычных систем линейных уравнений одним из известных методов. Однако такой способ является трудоемким, поскольку ведет к необходимости решения 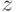штук систем, где

$z=w(B_1) \dots w(B_n)=\Pi_{i=1}^nw(B_i)$

Доказываемая ниже теорема позволяет значительно уменьшить трудоемкость нахождения всех решений системы (20.3).

Предварительно введем следующие обозначения:

$\{e_k\}= \begin {cases} 0, если i \ne k, 1, если i=k \end {cases}, k=\overline {1,0}; i=\overline {1,n} ;\\ \underline B=[\underline B_1, \underline B_2, \dots \underline B_n]',$

где

$\underline B_i=\alpha_i, \alpha_i \in B_i, \forall \beta_i \in B_i (\alpha \le \beta), i=\overline {1,n}$

Теорема 20.1. Пусть $(\xi_1, \dots, \xi_n)'$ есть решение системы

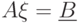$A \xi=\underline B$

( 20.4)

а $(\delta_1^{(k)}, \dots, \delta_n^{(k)})'$ есть решения n штук систем

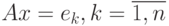$Ax=e_k, k=\overline {1,n}$

( 20.5)

Тогда решение $x=(x_1, \dots, x_n')$ системы (20.3) имеет вид

$x_j=\xi_j + \sum_{k=1}^n m_k \delta_j^{(k)}, j=\overline {1,n}$

( 20.6)

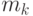где $\underline B_k+m_k \in B_k$ т. е. m_k пробегают независимо все значения от 0 до -1, при этом из них точно w(B_k)

Доказательство. Рассмотрим -ю строку системы (20.3):

$(Ax)_i=\sum_{j=1}^n a_{ij}x_j=\sum_{j=1}^n a_{ij} \left ( \xi_j +\sum_{k=1}^n m_k \delta_j^{(k)} \right )= \sum_{j=1}^n \left (a_{ij} \xi_j+ \sum_{k=1}^n m_k \delta_j^{(k)} \right )\\ =\sum_{j=1}^n a_{ij} \xi_j+\sum_{j=1}^n \sum_{k=1}^n m_k \delta_j^{(k)}= \underline B_i +\sum_{k=1}^n m_k \sum_{j=1}^n a_{ij}\delta_j^{(k)}= \underline B_1+m_i,$

поскольку

$\sum_{j=1}^{n}a_{ij}\delta_j^{(k)}= \begin {cases} 0, если i \ne k,\\ 1, если i=k \end {cases}$

Таким образом, $(Ax)_i=\underline B_i +m_i$ , a $\underline B_i+m_i \in B_i$ , следовательно, (Ax)_i=B_i , откуда и вытекает справедливость теоремы.

Из этой теоремы следует, что в действительности для построения всех решений системы (20.3) необходимо решить только 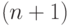(n+1) систему линейных уравнений, а не $w(B_1) \dots w(B_n)$ систем, как это было в тривиальном способе.