| Россия |
Обобщенные линейные автоматы без потери информации
Рассмотрим автоматы, у которых входы и выходы являются многоканальными, т. е. их входные и выходные алфавиты структурированы. Каждый из таких автоматов может не быть автоматом БПИ в классическом смысле, но вместе с тем он может допускать возможность восстановления некоторого подмножества компонент входного символа при наблюдении реакций на подмножестве его выходных каналов. Такого рода автоматы были исследованы в работах [48], [49] и названы обобщенными автоматами БПИ (ОБПИ).
В этой лекции будут исследованы обобщенные линейные автоматы БПИ. В частности, в терминах характеристических матриц ЛА будет получен критерий принадлежности автомата упомянутому классу.
Введем некоторые понятия, которые понадобятся далее.
Выходной канал  ЛА
ЛА  назовем избыточным, если в любой момент времени
назовем избыточным, если в любой момент времени  значение сигнала
значение сигнала  на нем есть линейная комбинация сигналов на остальных выходных каналах этого же автомата.
на нем есть линейная комбинация сигналов на остальных выходных каналах этого же автомата.
Линейный автомат назовем неизбыточным по выходам, если в нем отсутствуют избыточные выходные каналы.
Из сказанного выше следует, что множество 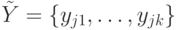 неизбыточных каналов представляет собой такое минимальное по мощности подмножество множества
неизбыточных каналов представляет собой такое минимальное по мощности подмножество множества  всех выходных каналов ЛА, значений сигналов на которых достаточно для определения значений сигналов на каналах из множества
всех выходных каналов ЛА, значений сигналов на которых достаточно для определения значений сигналов на каналах из множества  .
.
Теорема 16.1. Для того чтобы ЛА  был неизбыточным по выходам, необходимо и достаточно, чтобы число его выходных каналов было равно рангу матрицы
был неизбыточным по выходам, необходимо и достаточно, чтобы число его выходных каналов было равно рангу матрицы ![[C, D]](/sites/default/files/tex_cache/0cd352e3751e2f5b536b459f84da4e6b.png) системы (1.2) уравнений выходов этого автомата.
системы (1.2) уравнений выходов этого автомата.
Доказательство. Предположим, что ранг матрицы системы линейных уравнений (10.2) относительно неизвестных  равен
равен  , где
, где  . Известно [19], что это условие является необходимым и достаточным для того, чтобы
. Известно [19], что это условие является необходимым и достаточным для того, чтобы  уравнений упомянутой системы представляли собой линейные комбинации остальных уравнений. Применительно к линейному автомату этот факт означает, что
уравнений упомянутой системы представляли собой линейные комбинации остальных уравнений. Применительно к линейному автомату этот факт означает, что  его выходных каналов являются избыточными. Отсюда и вытекает справедливость теоремы.
его выходных каналов являются избыточными. Отсюда и вытекает справедливость теоремы.
Опишем общий метод, позволяющий определить избыточные выходные каналы в ЛА. Этот метод основан на применении известного метода Гаусса [33] для решения систем линейных алгебраических уравнений. Пусть Q - матрица системы (1.2). Методом Гаусса приведем матрицу  к ступенчатой форме. В процессе такого приведения некоторые строки могут вырождаться в нулевые, что свидетельствует о линейной зависимости соответствующих уравнений системы (10.2) от других уравнений. Очевидно, что выходные каналы ЛА, которым соответствуют нулевые строки в ступенчатой матрице, и являются избыточными.
к ступенчатой форме. В процессе такого приведения некоторые строки могут вырождаться в нулевые, что свидетельствует о линейной зависимости соответствующих уравнений системы (10.2) от других уравнений. Очевидно, что выходные каналы ЛА, которым соответствуют нулевые строки в ступенчатой матрице, и являются избыточными.
Проиллюстрируем изложенное на примере ЛА над полем 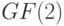 с характеристическими матрицами
с характеристическими матрицами
![C=
\left [
\begin {matrix}
1&0&0\\
0&1&0\\
0&1&1\\
0&0&1
\end {matrix}
\right ],
D=
\left [
\begin {matrix}
0&1&0\\
1&0&0\\
0&0&0\\
1&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/4b9424305d4704624b2a964f466d6c9d.png)
Преобразование методом Гаусса матрицы ![[C,D]](/sites/default/files/tex_cache/14da110218612ca7102f9a72645f2cb5.png) в данном случае осуществляется за два шага, и полученные при этом матрицы имеют вид
в данном случае осуществляется за два шага, и полученные при этом матрицы имеют вид
![\left [
\begin {matrix}
1&0&0&0&1&0\\
0&1&0&!&0&0\\
0&0&1&1&0&0\\
0&0&1&1&0&0
\end {matrix}
\right ]
\begin {matrix}
y_1\\
y_2\\
y_2\oplus y_3\\
y_4
\end {matrix}
\left [
\begin {matrix}
1&0&0&0&1&0\\
0&1&0&1&0&0\\
0&0&1&1&0&0\\
0&0&0&0&0&0
\end {matrix}
\right ]
\begin {matrix}
y_1\\
y_2\\
y_2 \oplus y_3\\
y_2 \oplus y_3 \oplus y_4
\end {matrix}](/sites/default/files/tex_cache/bdb13b4bbfcf71f561397dbc2698b335.png)
Равенство нулю четвертой строки последней матрицы означает, что ![y_2 \oplus y_3 \oplus y_4=[0]](/sites/default/files/tex_cache/ab44e9c36ccd5ce06ebf11fca4e34532.png) . Последнее равенство равносильно трем следующим:
. Последнее равенство равносильно трем следующим:  . Эти равенства говорят о том, что любой, но только один канал из множества
. Эти равенства говорят о том, что любой, но только один канал из множества  в действительности можно считать избыточным. В самом деле, значение сигнала на одном из упомянутых каналов есть линейная комбинация сигналов на двух других каналах из этой тройки.
в действительности можно считать избыточным. В самом деле, значение сигнала на одном из упомянутых каналов есть линейная комбинация сигналов на двух других каналах из этой тройки.
Теорема 16.2. Для того чтобы ЛА БПИ являлся неизбыточным по выходам, необходимо и достаточно, чтобы число его выходных каналов  было не меньше числа
было не меньше числа 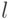 его входных каналов.
его входных каналов.
Доказательство.
Необходимость. Пусть ЛА  есть БПИ и не имеет избыточных выходов. Покажем, что тогда
есть БПИ и не имеет избыточных выходов. Покажем, что тогда  . Поскольку ЛА есть автомат БПИ, то по теореме 3.1
. Поскольку ЛА есть автомат БПИ, то по теореме 3.1  . На основании теоремы 16.1 неизбыточность ЛА по выходам равносильна условию
. На основании теоремы 16.1 неизбыточность ЛА по выходам равносильна условию ![\rank [C,D]=m](/sites/default/files/tex_cache/d1fce9740e3c4a72a87e249dde8bfc35.png) . Из определения ранга матрицы следует, что
. Из определения ранга матрицы следует, что ![\rank [C,D] \ge \rank D](/sites/default/files/tex_cache/caa5925c194dc22ba2130849a6dbc6a8.png) , т. е.
, т. е.  .
.
Достаточность. Пусть ЛА есть автомат БПИ и  . Докажем, что ЛА будет неизбыточен по выходам. Доказательство проведем от противного. Пусть
. Докажем, что ЛА будет неизбыточен по выходам. Доказательство проведем от противного. Пусть  . Нетрудно показать, что
. Нетрудно показать, что
![\rank [C,D] \ge \max [\rank C, \rank D]](/sites/default/files/tex_cache/33f481e41766aa7928eafe44d5dc8b2f.png) |
( 16.1) |
Поскольку ЛА есть БПИ, то  . С учетом неравенств
. С учетом неравенств  и
и  , получаем
, получаем
![\max [\rank C, \rank D]=l](/sites/default/files/tex_cache/86c219aea4739dcb264b90e72026145f.png)
Таким образом, из (16.1) следует, что ![\rank [C,D] \ge l](/sites/default/files/tex_cache/0ac83b8d5d0de1c1dd6dd66e81dfbae4.png) . Поскольку
. Поскольку  , то
, то ![\rank [C,D] \ne m](/sites/default/files/tex_cache/412e4ee1a4e83e194605279fa9dd1a4b.png) и по теореме 16.1 рассматриваемый ЛА является избыточным по выходам. Полученное противоречие завершает доказательство теоремы.
и по теореме 16.1 рассматриваемый ЛА является избыточным по выходам. Полученное противоречие завершает доказательство теоремы.
Введем теперь понятие обобщенного линейного автомата БПИ (ОБПИ).
Пусть 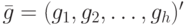 - вектор-столбец, представляющий собой входной символ ЛА;
- вектор-столбец, представляющий собой входной символ ЛА; 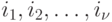 - некоторые натуральные числа, где
- некоторые натуральные числа, где  , если
, если 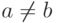 и
и  . Назовем проекцией вектора
. Назовем проекцией вектора  по входным каналам
по входным каналам  вектор-столбец
вектор-столбец  и обозначим ее как
и обозначим ее как  . Пусть
. Пусть  - упорядоченная последовательность вектор-столбцов, которую будем называть входным словом. Тогда проекцией слова
- упорядоченная последовательность вектор-столбцов, которую будем называть входным словом. Тогда проекцией слова 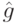 по каналам
по каналам  назовем упорядоченную последовательность вектор-столбцов
назовем упорядоченную последовательность вектор-столбцов 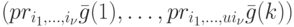 .
.
Рассмотрим следующую задачу. На ЛА  , находящийся в известном начальном состоянии
, находящийся в известном начальном состоянии  , подается неизвестное входное слово
, подается неизвестное входное слово 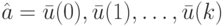 и по выходным каналам с номерами
и по выходным каналам с номерами  , где
, где  наблюдается выходная реакция. Требуется распознать проекцию слова
наблюдается выходная реакция. Требуется распознать проекцию слова  по каналам с номерами
по каналам с номерами 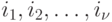 , где
, где 
Условимся далее через  , где
, где  , обозначать такой подавтомат ЛА
, обозначать такой подавтомат ЛА  , у которого:
, у которого:
- множество состояний, входной и выходной алфавиты и функция переходов те же, что у ЛА
 ;
; - выходной символ подавтомата в момент времени
 есть
есть  , где
, где 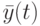 - выходной символ ЛА
- выходной символ ЛА  в тот же момент времени.
в тот же момент времени.
Понятно, что решение сформулированной выше задачи сводится к выяснению того, существует ли для заданного ЛА  такой подавтомат
такой подавтомат  , для которого восстановление
, для которого восстановление  по наблюдаемой реакции
по наблюдаемой реакции  возможно независимо от входного слова
возможно независимо от входного слова  и действительного начального состояния ЛА
и действительного начального состояния ЛА  .
.
Далее такой подавтомат  ) будем называть обобщенным без потери информации (ОБПИ).
) будем называть обобщенным без потери информации (ОБПИ).
Существование у ЛА  подавтомата ОБПИ
подавтомата ОБПИ  содержательно означает, что исходный ЛА, не являясь автоматом БПИ в классическом смысле, тем не менее позволяет восстановить фрагменты его неизвестных входных слов по наблюдаемым фрагментам выходных слов и известному начальному состоянию.
содержательно означает, что исходный ЛА, не являясь автоматом БПИ в классическом смысле, тем не менее позволяет восстановить фрагменты его неизвестных входных слов по наблюдаемым фрагментам выходных слов и известному начальному состоянию.
Перейдем теперь к описанию процедуры, с помощью которой для заданного ЛА и заданного подмножества его выходных каналов можно установить, существует ли в ЛА такое подмножество  его входных каналов, что подавтомат
его входных каналов, что подавтомат  является ОБПИ.
является ОБПИ.
Условимся далее выходные каналы с номерами из подмножества  называть наблюдаемыми, а каналы с номерами из подмножества
называть наблюдаемыми, а каналы с номерами из подмножества  - ненаблюдаемыми.
- ненаблюдаемыми.
Пусть 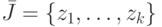 , т. е. выходные каналы с номерами
, т. е. выходные каналы с номерами  - ненаблюдаемые. Условимся, что строки всех характеристических матриц ЛА пронумерованы числами
- ненаблюдаемые. Условимся, что строки всех характеристических матриц ЛА пронумерованы числами  сверху вниз, а столбцы - числами
сверху вниз, а столбцы - числами  слева направо. Напомним, что строкам
слева направо. Напомним, что строкам  матриц
матриц  и
и  и столбцам
и столбцам  ,h матриц
,h матриц  и
и  соответствуют компоненты
соответствуют компоненты 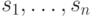 вектор-состояния, строкам
вектор-состояния, строкам  m матриц
m матриц  и столбцам
и столбцам  матриц
матриц  и
и  - компоненты
- компоненты  входного вектора
входного вектора 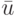 .
.
Перейдем теперь к описанию упомянутой выше процедуры.
- В матрице
 вычеркиваются строки, соответствующие ненаблюдаемым выходам
вычеркиваются строки, соответствующие ненаблюдаемым выходам 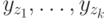 . Оставшуюся часть матрицы размерности
. Оставшуюся часть матрицы размерности  обозначим через
обозначим через  . Находим в ней подматрицу с максимальным рангом, который обозначим через
. Находим в ней подматрицу с максимальным рангом, который обозначим через  . Пусть
. Пусть  - переменные, соответствующие столбцам подматрицы с максимальным рангом
- переменные, соответствующие столбцам подматрицы с максимальным рангом  , которые будем называть потенциально восстанавливаемыми. Вычеркнем из
, которые будем называть потенциально восстанавливаемыми. Вычеркнем из  столбцы, соответствующие переменным
столбцы, соответствующие переменным  , и полученную матрицу обозначим
, и полученную матрицу обозначим ![[D_J]](/sites/default/files/tex_cache/e47fae41bfb158f89da40781960c4910.png) . Если
. Если ![[DJ] = [0]](/sites/default/files/tex_cache/3ca3ad72f8dfcb01824f5464e6ad3a45.png) , то перейдем к пункту 2, иначе процедура завершается - при удалении выходов
, то перейдем к пункту 2, иначе процедура завершается - при удалении выходов 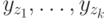 не существует такого подмножества выходов
не существует такого подмножества выходов  , что подавтомат
, что подавтомат  является ОБПИ.
является ОБПИ. - В матрице C вычеркиваются строки, соответствующие ненаблюдаемым выходам
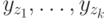 . Оставшуюся часть матрицы обозначим через
. Оставшуюся часть матрицы обозначим через 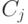 . Пусть
. Пусть  - переменные, которым соответствуют столбцы в матрице
- переменные, которым соответствуют столбцы в матрице 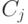 , содержащие нулевые элементы. Очевидно, что
, содержащие нулевые элементы. Очевидно, что  - компоненты вектор-состояния, которые необходимо знать для вычисления по известной реакции неизвестных компонент
- компоненты вектор-состояния, которые необходимо знать для вычисления по известной реакции неизвестных компонент  выходного вектора. Переходим далее к пункту 3 процедуры.
выходного вектора. Переходим далее к пункту 3 процедуры. - В матрице
 выделим строки, соответствующие компонентам
выделим строки, соответствующие компонентам  вектор-состояния, и полученную матрицу обозначим через
вектор-состояния, и полученную матрицу обозначим через 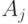 Вычеркнем из нее столбцы, соответствующие переменным
Вычеркнем из нее столбцы, соответствующие переменным  , в результате чего получим матрицу
, в результате чего получим матрицу ![[A_J]](/sites/default/files/tex_cache/405cc71691f630aa3fee7b5472afde58.png) . Если
. Если ![[A_J] = [0]](/sites/default/files/tex_cache/9a6560486a1c262ae460a26f799f5573.png) , то перейдем к пункту 4, иначе процедура завершается - при выходах
, то перейдем к пункту 4, иначе процедура завершается - при выходах 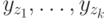 не существует такого подмножества выходов
не существует такого подмножества выходов  , что подавтомат
, что подавтомат  является ОБПИ.
является ОБПИ. - В матрице
 выделим строки, соответствующие компонентам
выделим строки, соответствующие компонентам  , и полученную матрицу обозначим через
, и полученную матрицу обозначим через  . Вычеркнем из нее столбцы, соответствующие переменным
. Вычеркнем из нее столбцы, соответствующие переменным  , в результате чего получим матрицу
, в результате чего получим матрицу 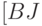 ]. Если
]. Если ![[BJ] = [0]](/sites/default/files/tex_cache/cecbeaf50e3203b30f3b0d6ca39e095f.png) , то подавтомат
, то подавтомат  , где
, где  является ОБПИ, иначе в ЛА при заданном J не существует подавтомата ОБПИ. На этом процедура свою работу завершает.
является ОБПИ, иначе в ЛА при заданном J не существует подавтомата ОБПИ. На этом процедура свою работу завершает.
Описанная процедура позволяет не только определить, существует ли такое множество  , что подавтомат
, что подавтомат  является ОБПИ, но и установить состав множества
является ОБПИ, но и установить состав множества  . Построенный подавтомат
. Построенный подавтомат  имеет в качестве входного вектор
имеет в качестве входного вектор ![[\tilde {u_1}, \dots, \tilde {u_q}]'](/sites/default/files/tex_cache/5393bb3200b98b50d1e3dd4308658c84.png) , в качестве выходного вектор
, в качестве выходного вектор ![[y_{j_i}, \dots, y_{j_{\mu}}]'](/sites/default/files/tex_cache/a98fdda94c39b78dddafb5ba8ca27e2e.png) , в качестве вектор-состояния
, в качестве вектор-состояния ![[\tilde {s_1}, \dots, \tilde {s_h}]'](/sites/default/files/tex_cache/447dc73620580595e23ed417bf68a297.png) , а его характеристическими матрицами являются матрицы
, а его характеристическими матрицами являются матрицы  , из которых удалены все строки и столбцы, за исключением тех, которые соответствуют множествам переменных
, из которых удалены все строки и столбцы, за исключением тех, которые соответствуют множествам переменных  .
.
Прокомментируем описанную процедуру. Условие ![{D_j}=[0]](/sites/default/files/tex_cache/fad3372b86bcf3c888d60aed25becfb0.png) в пункте 1 процедуры означает, что при вычислении реакций подавтомата
в пункте 1 процедуры означает, что при вычислении реакций подавтомата  используются только потенциально восстанавливаемые переменные
используются только потенциально восстанавливаемые переменные  и никакие другие. Условия
и никакие другие. Условия ![[A_j]=[0]](/sites/default/files/tex_cache/a151d57b0b8ddebbd641966576f345e3.png) и
и ![[B_j]=[0]](/sites/default/files/tex_cache/bf7ab2aa2e8fd78ca21f10069a7a0be2.png) в пунктах 3, 4 процедуры означают, что при вычислении компонент
в пунктах 3, 4 процедуры означают, что при вычислении компонент  следующего состояния подавтомата
следующего состояния подавтомата  по формуле (1.1) в составляющей
по формуле (1.1) в составляющей  задействуются только эти же компоненты, а в составляющей
задействуются только эти же компоненты, а в составляющей 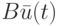 - только потенциально восстанавливаемые компоненты
- только потенциально восстанавливаемые компоненты  входного вектора.
входного вектора.
Учитывая эти комментарии, несложно провести строгое обоснование описанной процедуры.
Из описанной процедуры, с учетом использованных в ней обозначений, вытекает справедливость следующего утверждения.

