| Россия |
Эксперименты с автоматами, имеющими взвешенный входной алфавит
Синтез синхронизирующих последовательностей, минимальных по весу
В основе построения СП, УП и ДП, минимальных по весу, лежит так называемое дерево преемников, формируемое для автомата  и множества
и множества 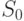 его допустимых начальных состояний. Оно незначительно отличается от аналогичной структуры, определенной в [18]. Остановимся на способе его построения.
его допустимых начальных состояний. Оно незначительно отличается от аналогичной структуры, определенной в [18]. Остановимся на способе его построения.
Под  -множеством автомата
-множеством автомата  понимается любая конечная совокупность состояний
понимается любая конечная совокупность состояний  , не все из которых обязательно различны. Если
, не все из которых обязательно различны. Если  -множество содержит один элемент, то оно называется простым. Если
-множество содержит один элемент, то оно называется простым. Если  -множество содержит два или более одинаковых элементов, оно именуется кратным.
-множество содержит два или более одинаковых элементов, оно именуется кратным.  -множество однородно, если все его элементы совпадают друг с другом.
-множество однородно, если все его элементы совпадают друг с другом.
Назовем  -группой множество, состоящее из
-группой множество, состоящее из  -множеств, общее число элементов которых равно
-множеств, общее число элементов которых равно  .
.  -группа называется простой (однородной), если все
-группа называется простой (однородной), если все  -множества в ней просты (однородны).
-множества в ней просты (однородны).
Пусть  есть
есть  -группа, состоящая из
-группа, состоящая из  -множеств
-множеств  -преемник
-преемник  есть другая
есть другая  -группа, построенная по следующим правилам:
-группа, построенная по следующим правилам:
-
 -множество
-множество  разбиваем на такие подмножества, каждое из которых содержит все те состояния из
разбиваем на такие подмножества, каждое из которых содержит все те состояния из  , которые вырабатывают одинаковую реакцию на входную последовательность
, которые вырабатывают одинаковую реакцию на входную последовательность  . Каждое полученное подмножество далее интерпретируется как
. Каждое полученное подмножество далее интерпретируется как  -множество, а совокупность всех таких подмножеств интерпретируется как
-множество, а совокупность всех таких подмножеств интерпретируется как  -группа
-группа  .
. - В
 -множествах из
-множествах из  заменяем каждое состояние его преемником относительно входной последовательности
заменяем каждое состояние его преемником относительно входной последовательности  .
.
Получаемая в результате такого построения  -группа является
-группа является  -преемником
-преемником  .
.
Определим теперь структуру, называемую деревом преемников для заданного автомата  и множества допустимых начальных состояний
и множества допустимых начальных состояний 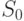 . Она состоит из ветвей, расположенных в последовательных уровнях, нумерация которых начинается с нуля. Нулевой уровень дерева содержит единственную, называемую начальной, ветвь. Условимся считать, что она связана с
. Она состоит из ветвей, расположенных в последовательных уровнях, нумерация которых начинается с нуля. Нулевой уровень дерева содержит единственную, называемую начальной, ветвь. Условимся считать, что она связана с  -группой
-группой 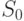 . Если входной алфавит
. Если входной алфавит 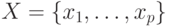 автомата
автомата  содержит
содержит  символов, то каждая ветвь в
символов, то каждая ветвь в  -м уровне
-м уровне  расщепляется на
расщепляется на  ветвей, представляющих символы
ветвей, представляющих символы  соответственно и являющихся ветвями
соответственно и являющихся ветвями  -го уровня. Ветвь
-го уровня. Ветвь 
 -го уровня считается связанной с
-го уровня считается связанной с  -группой, являющейся
-группой, являющейся  -приемником соответствующей
-приемником соответствующей  -группы уровня
-группы уровня  . Будем называть вершины простыми, кратными или однородными, если они связаны с соответствующими
. Будем называть вершины простыми, кратными или однородными, если они связаны с соответствующими  -группами.
-группами.
Из описанного метода построения вытекает, что дерево преемников является бесконечной структурой. Для синтеза СП, УП и ДП нами будут из упомянутой бесконечной структуры выделяться конечные деревья за счет введения специальных правил обрыва ветвей. Каждая такая оборванная ветвь связана с вершиной дерева, которую мы будем называть листом, следуя терминологии, принятой в теории графов.
Для построения минимальной по весу СП используем граф, который назовем синхронизирующим деревом (СД). Основой для его построения является описанное выше дерево преемников.
Вершинами СД являются  -группы дерева преемников. Корень СД представляет собой
-группы дерева преемников. Корень СД представляет собой  -группу
-группу 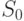 нулевого уровня. Вершиной 1-го уровня СД, связанной с
нулевого уровня. Вершиной 1-го уровня СД, связанной с  -ветвью, является
-ветвью, является  -группа
-группа  , представляющая собой
, представляющая собой  -преемник
-преемник  -группы
-группы 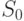 , при этом из вершины
, при этом из вершины 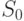 в
в  проводится дуга, помеченная символом
проводится дуга, помеченная символом  . Аналогично строятся вершины СД всех последующих уровней и соединяющие их дуги. Каждой вершине
. Аналогично строятся вершины СД всех последующих уровней и соединяющие их дуги. Каждой вершине  в СД поставим в соответствие флажок (на рисунках он будет обозначаться прямоугольником), в него будет вписано число, равное сумме весов входных символов последовательности, которая соответствует пути по СД, ведущему из корня в вершину
в СД поставим в соответствие флажок (на рисунках он будет обозначаться прямоугольником), в него будет вписано число, равное сумме весов входных символов последовательности, которая соответствует пути по СД, ведущему из корня в вершину  .
.
Условимся теперь об обозначениях вершин СД. Если вершине  СД соответствует
СД соответствует  -группа
-группа  , где
, где  -
-  -множества, то для ее обозначения будем использовать множество состояний автомата
-множества, то для ее обозначения будем использовать множество состояний автомата  , равное
, равное

Для того чтобы выделить из дерева преемников конечное СД, введем правила обрыва ветвей. Правила эти должны определять момент, когда некоторая вершина дерева преемников становится листом, то есть из нее в процессе дальнейшего построения не исходит никаких дуг.
При построении СД автомата  с множеством
с множеством 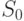 допустимых начальных состояний вершина
допустимых начальных состояний вершина 
 -го уровня становится листом, если выполняется хотя бы одно из следующих условий:
-го уровня становится листом, если выполняется хотя бы одно из следующих условий:
-
 ;
; - на уровнях, предшествующих
 -му, имеется такая вершина
-му, имеется такая вершина  , что
, что  , но значение флажка вершины
, но значение флажка вершины  больше значения флажка вершины
больше значения флажка вершины  ;
; - на уровнях, предшествующих
 -му, имеется такая вершина
-му, имеется такая вершина  , что
, что  , а значение флажка вершины
, а значение флажка вершины  больше значения флажка вершины
больше значения флажка вершины  .
.
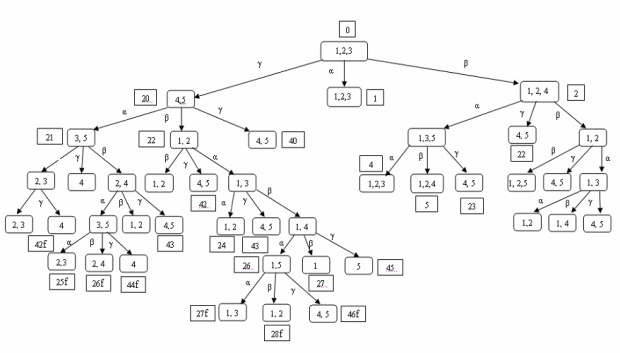
Проиллюстрируем процесс построения СД для автомата, заданного табл. 1.1, считая, что 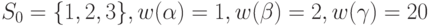 . Этот граф приведен на рис. 1.1. В овале, изображающем вершину, перечислены состояния множества, соответствующего этой вершине.
. Этот граф приведен на рис. 1.1. В овале, изображающем вершину, перечислены состояния множества, соответствующего этой вершине.
| s\x |  |
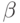 |
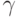 |
|---|---|---|---|
| 1 | 1/0 | 1/1 | 5/0 |
| 2 | 3/1 | 2/0 | 4/0 |
| 3 | 2/1 | 4/1 | 4/0 |
| 4 | 5/1 | 1/1 | 5/1 |
| 5 | 3/0 | 2/0 | 4/1 |
Так, вершина 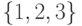 первого уровня, две вершины
первого уровня, две вершины  второго уровня, вершины
второго уровня, вершины  и
и  третьего уровня и т. д. являются листьями в силу пункта 2 правил обрыва. Вершины
третьего уровня и т. д. являются листьями в силу пункта 2 правил обрыва. Вершины 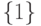 и
и 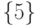 пятого уровня, вершина
пятого уровня, вершина 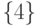 третьего уровня являются листьями в силу пункта 1 правил обрыва. Две вершины
третьего уровня являются листьями в силу пункта 1 правил обрыва. Две вершины  четвертого уровня, имеющие значение флажка 43, являются листьями в силу пункта 3 тех же правил.
четвертого уровня, имеющие значение флажка 43, являются листьями в силу пункта 3 тех же правил.
Из способа построения СД вытекает, что последовательность входных символов, соответствующая пути по СД из корня в одну из вершин  , где
, где  , является СП для заданного автомата.
, является СП для заданного автомата.
Понятно, что построение минимальной по весу СП сводится к следующей простой процедуре. Среди всех вершин  СД, у которых
СД, у которых  , отыскивается вершина с минимальным значением флажка
, отыскивается вершина с минимальным значением флажка  и в СД находится путь в нее из корня дерева. Очевидно, что соответствующая этому пути последовательность символов и является СП, имеющей минимальный вес, равный упомянутому значению флажка
и в СД находится путь в нее из корня дерева. Очевидно, что соответствующая этому пути последовательность символов и является СП, имеющей минимальный вес, равный упомянутому значению флажка  .
.
Так, в СД на рис1.1 имеется 4 таких вершины, из которых вершина 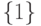 пятого уровня имеет минимальное значение флажка, равное 27.
пятого уровня имеет минимальное значение флажка, равное 27.
Поскольку пути из корня в эту вершину соответствует входная последовательность  , то она и является минимальной по весу СП. Заметим, кстати, что минимальной по длине СП для этого автомата и того же множества допустимых начальных состояний является последовательность
, то она и является минимальной по весу СП. Заметим, кстати, что минимальной по длине СП для этого автомата и того же множества допустимых начальных состояний является последовательность 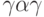 , соответствующая пути по СД из корня в вершину
, соответствующая пути по СД из корня в вершину 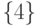 третьего уровня.
третьего уровня.
Приведенный пример показывает, что в общем случае СП для автомата может быть минимальной по весу, но не являться минимальной по длине.