Моделирование ситуаций и разработка решений
8.3.6. Характеристика способов принятия решений на основе оптимизации показателей
Способы принятия решений на основе оптимизации показателей связаны с нахождением, исходя из имеющихся зависимостей различных факторов между собой и заданных ограничений, наиболее рационального варианта.
Так, например, методы задач линейного программирования связаны с нахождением наилучшей программы управленческих действий в случае, когда в качестве целевой функции и ограничений выступают линейные зависимости, в которых неизвестные находятся в первой степени.
Постановка задачи линейного программирования носит экстремальный характер, т. е. состоит в нахождении таких значений переменных величин, при которых целевая функция достигает максимума или минимума в зависимости от характера задачи.
Порядок разработки модели линейного программирования рассмотрим на примере.
Пусть требуется разработать план производства двух изделий при обеспечении наиболее целесообразного использования трех видов ограниченных ресурсов. Выгодность плана будем оценивать суммой прибыли, которую получит предприятие от реализации продукции.
Введем обозначения. Искомое количество изделий видов I и II обозначим x1 и x2. Норма расхода первого вида ресурса А1 на изделие I - a11 (табл. 8.1), второго вида ресурса А2 на изделие I - a12 и т. д. Лимит по каждому виду ресурса обозначим b1, b2, b3, прибыль за единицу реализованной продукции d1 и d2. Логическая схема решения задачи составляется с помощью табл. 8.2.
| Изделие | Норма расхода ресурсов на одно изделие | Прибыль от реализации одного изделия | ||
|---|---|---|---|---|
|
А1 |
А2 |
А3 |
||
|
I |
a11 |
a12 |
a13 |
d1 |
|
II |
a21 |
a22 |
a23 |
d2 |
| Лимит на ресурс |
b1 |
b2 |
b3 |
|
Запишем систему ограничений для выпуска изделий видов I и II:

Условие (8.1) представляет собой систему ограничений и означает, что расход каждого из трех видов ресурсов не может превышать лимита.
Кроме ограничений по объему потребляемых ресурсов, могут быть заданы условия, в соответствии с которыми фиксируется минимальный объем выпуска тех или иных изделий. Выпуск продукции физически не может быть отрицательным. Это дополнительное ограничение:
x1 > 0, x2 > 0. (8.2)
Поскольку задача сводится к нахождению таких объемов выпуска продукции, при которых прибыль будет максимальной, целевую функцию можно записать в виде:
 . (8.3)
. (8.3)
На практике может стоять задача и минимизации целевой функции (например, минимизация себестоимости выпуска продукции).
Все разновидности таких задач сводятся к основной задаче линейного программирования (ОЗЛП). Эта задача характеризуется тем, что ограничения-неравенства приводятся к равенствам, а целевая функция обращается в экстремум.
В теории массового обслуживания в качестве критерия эффективности системы массового обслуживания (СМО) используется значение функции потерь, которая для одноканального варианта системы имеет вид:
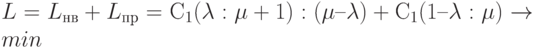 , (8.4)
, (8.4)
| где |
Lнв |
- | потери от недополученной выгоды; |
|
Lпр |
- | потери от простоя; | |
|
C1 |
- | стоимость одной заявки, ожидающей обслуживания в системе; | |
|
C2 |
- | стоимость содержания единицы пропускной способности СМО в единицу времени; | |
|
|
- | интенсивность потока требований на обслуживание; | |
|
|
- | интенсивность обслуживания требований системой. |
Функция потерь для многоканального (двух- и трехканального) варианта СМО имеет вид:

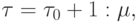
![\tau_0 = P_0(\lambda : \mu)^{S + 1} : [\lambda(S - 1)!(S - \rho)^2]](/sites/default/files/tex_cache/67f246cc3fb782d436246c4c28ff4b3d.png)

| S | - | количество каналов обслуживания в системе, | |
|
S0 |
среднее число незанятых каналов в системе обслуживания. |
Теория игр исследует с помощью математического аппарата ситуации, в которых принятие решений зависит от возможностей нескольких участников. Интересы участников могут быть как антагонистические (полностью противоположные), так и неантагонистические. В последнем случае может исследоваться вопрос о наиболее эффективных совместных действиях, изучаемых в рамках кооперативных игр.
Понятие риска предполагает наличие рискующего - лицо, принимающее решение (ЛПР).
Допустим, рассматривается вопрос о проведении финансовой операции в условиях неопределенности. При этом у ЛПР есть несколько возможных решений i = 1, 2, ..., m, а реальная ситуация неопределенна и может принимать один из вариантов j = 1, 2, ..., n. Пусть известно, что если ЛПР примет i-e решение, а ситуация примет j-й вариант, то будет получен доход qij. Матрица Q = (qij) называется матрицей последствий (возможных решений или платежной матрицей).
Оценим размеры риска в данной схеме.
Пусть принимается i-е решение. Очевидно, если бы было известно, что реальная ситуация будет j-я, то ЛПР принял бы решение, дающее доход  Однако i-е решение принимается в условиях неопределенности. Значит, ЛПР рискует получить не qj , а только qij. Таким образом, существует реальная возможность недополучить доход, и этому неблагоприятному исходу можно сопоставить риск rij, размер которого целесообразно оценить как разность
Однако i-е решение принимается в условиях неопределенности. Значит, ЛПР рискует получить не qj , а только qij. Таким образом, существует реальная возможность недополучить доход, и этому неблагоприятному исходу можно сопоставить риск rij, размер которого целесообразно оценить как разность
rij = qj - qij. (8.6)
Матрица R = (rij) называется матрицей рисков.
Например, используя формулу (8.6), составим матрицу рисков R = (rij) по заданной матрице последствий

Очевидно,  аналогично q2 = 5, q3 = 8, q4 = 12. Следовательно, матрица рисков имеет вид
аналогично q2 = 5, q3 = 8, q4 = 12. Следовательно, матрица рисков имеет вид

Полная неопределенность означает отсутствие информации о вероятностных состояниях среды ("природы"), например, о вероятностях тех или иных вариантов реальной ситуации; в лучшем случае известны диапазоны значений рассматриваемых величин. Рекомендации по принятию решений в таких ситуациях сформулированы в виде определенных правил (критериев). Рассмотрим основные из критериев.
Правило максимакса. По этому критерию определяется вариант решения, максимизирующий максимальные выигрыши - например, доходы - для каждого варианта ситуации. Это критерий крайнего ("розового", или легкомысленного) оптимизма, по которому наилучшим является решение, дающее максимальный выигрыш, равный 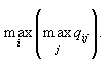 Рассматривая i-е решение, предполагают самую хорошую ситуацию, приносящую доход
Рассматривая i-е решение, предполагают самую хорошую ситуацию, приносящую доход  а затем выбирают решение с наибольшим ai.
а затем выбирают решение с наибольшим ai.
Для платежной матрицы в рассмотренном примере находим последовательность значений  a2 = 12, a3 = 10, a4 = 8. Из этих значений находим наибольшее: a2 = 12. Следовательно, критерий максимакса рекомендует принять второе решение (i = 2).
a2 = 12, a3 = 10, a4 = 8. Из этих значений находим наибольшее: a2 = 12. Следовательно, критерий максимакса рекомендует принять второе решение (i = 2).
Правило Вальда (правило максимина, или критерий крайнего пессимизма). Рассматривая i-e решение, будем полагать, что на самом деле ситуация складывается самая плохая, т. е. приносящая самый малый доход: bi = minqij. Но теперь выберем решение i0 с наибольшим  . Итак, правило Вальда рекомендует принять решение i0 такое, что
. Итак, правило Вальда рекомендует принять решение i0 такое, что 
В рассматриваемом примере имеем b1 = 2, b2 = 2, b3 = 3, b4 = 1. Теперь из этих значений выбираем максимальное b3 = 3. Значит, правило Вальда рекомендует принять третье решение i = 3).
Правило Сэвиджа (критерий минимаксного риска). Этот критерий аналогичен предыдущему критерию Вальда, но ЛПР принимает решение, руководствуясь не матрицей последствий Q, а матрицей рисков R = (rij). По этому критерию лучшим является решение, при котором максимальное значение риска будет наименьшим, т. е. равным  Рассматривая i-e решение, предполагают ситуацию максимального риска
Рассматривая i-e решение, предполагают ситуацию максимального риска  и выбирают вариант решения i0 с наименьшим
и выбирают вариант решения i0 с наименьшим 
Рассматривая матрицу рисков R для данного примера, находим последовательность величин  r2 = 6, r3 = 5, r4 = 7. Из этих величин выбираем наименьшую: r3 = 5. Значит, правило Сэвиджа рекомендует принять третье решение (i = 3). Заметьте, что это совпадает с выбором по критерию Вальда.
r2 = 6, r3 = 5, r4 = 7. Из этих величин выбираем наименьшую: r3 = 5. Значит, правило Сэвиджа рекомендует принять третье решение (i = 3). Заметьте, что это совпадает с выбором по критерию Вальда.
Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). По данному критерию выбирается вариант решения, при котором достигается максимум выражения  , где
, где  . Таким образом, этот критерий рекомендует руководствоваться некоторым средним результатом между крайним оптимизмом и крайним пессимизмом. При \lambda = 0 критерий Гурвица совпадает с максимаксным критерием, а при
. Таким образом, этот критерий рекомендует руководствоваться некоторым средним результатом между крайним оптимизмом и крайним пессимизмом. При \lambda = 0 критерий Гурвица совпадает с максимаксным критерием, а при  он совпадает с критерием Вальда. Значение
он совпадает с критерием Вальда. Значение  выбирается из субъективных (интуитивных) соображений.
выбирается из субъективных (интуитивных) соображений.
Для приведенной в рассмотренном примере матрицы последствий выберем наилучший вариант решения на основе критерия Гурвица при 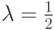 .
.
Рассматривая матрицу последствий Q по строкам, для каждого i вычисляем значения ci = 1 : 2minqij + 1 : 2maxqij. Например,  ; аналогично находятся с2 = 7; с3 = 6,5; с4 = 4,5. Наибольшим является с2 =7. Следовательно, критерий Гурвица при заданном
; аналогично находятся с2 = 7; с3 = 6,5; с4 = 4,5. Наибольшим является с2 =7. Следовательно, критерий Гурвица при заданном 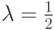 рекомендует выбрать второй вариант (i = 2).
рекомендует выбрать второй вариант (i = 2).
Правило Лапласа (критерий максимума средневзвешенного выигрыша). По данному критерию выбирается вариант решения, при котором для платежной матрицы достигается максимум выражения 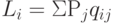 , где Рj - вероятность реализации j-ой ситуации, qij - значение выигрыша при реализации i-го решения при j-й ситуации:
, где Рj - вероятность реализации j-ой ситуации, qij - значение выигрыша при реализации i-го решения при j-й ситуации:

Таким образом, этот критерий рекомендует руководствоваться тем результатом, который обеспечивает средний максимальный выигрыш. Если вероятности реализации каждой j-й ситуации Рj заранее неизвестны, то в частном случае их можно считать равными между собой: Рj = 1/n, где n - число возможных ситуаций по платежной матрице.
На практике ситуации, в которых вероятности реализации каждой j-й ситуации Рj априорно (заранее) известны - крайне редки. Но и ситуации, в которых о возможностях реализации той или иной j-й ситуации заранее неизвестно ничего - также крайне редки. Чаще всего о возможностях реализации j-х ситуаций известна лишь некоторая информация, по которой можно провести ранжирование этих ситуаций, установив порядок их ожидаемой очередности. В этом случае вероятность реализации каждой из j-х ситуаций определяется выражением:

Для приведенной в рассмотренном примере платежной матрицы выберем наилучший вариант решения на основе критерия Лапласа, считая, что наибольшие шансы на реализацию имеет третья ситуация и далее, в порядке очередности - вторая, четвертая и первая, т. е. k1 = 4, k2 = 2, k3 = 1, k4 = 3.
Рассматривая платежную матрицу (матрицу последствий) Q по строкам, для каждого i вычисляем значения 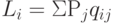 , предварительно вычислив значения Рj.
, предварительно вычислив значения Рj.
Например, Р1 = [2 x (n – k1 + 1)] : [n x (n + 1)] = [2 x (4 – 4 + 1)] : [4 x (4 + 1)] = 2 : 20 = 0,1.
Вычисляем аналогично Р2 = 0,3, Р3 = 0,4, Р4 = 0,2.
Тогда L1 = 0,1 x 5 + 0,3 x 2 + 0,4 x 8 + 0,2 x 4 = 5,1; аналогично находим L2 = 5,1; L3 = 5,5; L4 = 3,7. Наибольшим является L3 = 5,5. Следовательно, критерий Лапласа при указанном ранжировании j-х ситуации рекомендует выбрать второй вариант (i = 3).