|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Машины Тьюринга
Универсальная тьюрингова программа и пример невычислимой функции
В этом параграфе речь пойдет об универсальной тьюринговой
программе  , которая может имитировать любую программу, работающую над
фиксированным алфавитом
, которая может имитировать любую программу, работающую над
фиксированным алфавитом  .
Эта программа
.
Эта программа  , получив на входе псевдослово, содержащее
в определенном виде код произвольной программы
, получив на входе псевдослово, содержащее
в определенном виде код произвольной программы  и
псевдослово
и
псевдослово  , должна оставить на ленте код программы
, должна оставить на ленте код программы  и псевдослово
и псевдослово  —
результат работы программы
—
результат работы программы  на псевдослове
на псевдослове  .
.
Читатель, построивший универсальную программу, может считать себя изобретателем компьютера.
Пусть 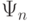 — множество всех функций
из
— множество всех функций
из  в
в  таких, что
каждая из них определена в точке 0 и вычислима программой, состоящей не
более чем из
таких, что
каждая из них определена в точке 0 и вычислима программой, состоящей не
более чем из  тьюринговых команд. Рассмотрим функцию
тьюринговых команд. Рассмотрим функцию 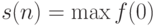 , где максимум берется по всем функциям из
, где максимум берется по всем функциям из 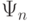 .
Очевидно,
.
Очевидно,  всюду определена и монотонна. Более того,
справедлива
всюду определена и монотонна. Более того,
справедлива
Теорема.
Для любой всюду определенной вычислимой функции  существует
существует  такое, что при любом
такое, что при любом  выполняется неравенство
выполняется неравенство  .
.
Действительно, пусть 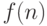 — произвольная всюду
определенная функция из
— произвольная всюду
определенная функция из  в
в  , тогда очевидно, что функция
, тогда очевидно, что функция

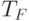 , состоящая из
, состоящая из  команд.
Рассмотрим программу
команд.
Рассмотрим программу ![T = [[1, r]^n, T_F]](/sites/default/files/tex_cache/151f5ab522c47bf868b13001c0c73759.png) ,
которая сначала записывает на ленте число
,
которая сначала записывает на ленте число  , а затем работает
как
, а затем работает
как 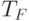 . Очевидно, что она состоит из
. Очевидно, что она состоит из  команд
и вычисляет некоторую функцию
команд
и вычисляет некоторую функцию  .
.По определению 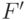 и
и  имеем
имеем  .
Используя монотонность функции
.
Используя монотонность функции  , получим
, получим  при всех
при всех  , следовательно,
, следовательно,  ,
,  . Отсюда следует, что при
. Отсюда следует, что при 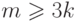 выполняется неравенство
выполняется неравенство  , что и требовалось доказать.
, что и требовалось доказать.
Следствие.
Функция  невычислима, так как она растет
быстрее, чем любая вычислимая функция.
невычислима, так как она растет
быстрее, чем любая вычислимая функция.
Заметим, что при любом фиксированном  значение
значение  можно попытаться вычислить путем перебора всех программ
длины
можно попытаться вычислить путем перебора всех программ
длины  и определения для каждой из них времени работы до момента остановки или
доказательства ее незавершаемости. Но вопрос о завершаемости программ
в общем виде алгоритмически неразрешим. Уточним основные моменты этого утверждения.
и определения для каждой из них времени работы до момента остановки или
доказательства ее незавершаемости. Но вопрос о завершаемости программ
в общем виде алгоритмически неразрешим. Уточним основные моменты этого утверждения.
Пусть  — тьюрингова программа, работающая в алфавите
— тьюрингова программа, работающая в алфавите  , и пусть
, и пусть 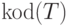 — слово в алфавите
— слово в алфавите  ,
кодирующее программу
,
кодирующее программу  (на деталях кодирования не останавливаемся).
(на деталях кодирования не останавливаемся).
Программа  называется самоприменимой, если при подаче ей на
вход ее собственного кода она через конечное число шагов остановится, в противном
случае программа называется несамоприменимой. Пусть
называется самоприменимой, если при подаче ей на
вход ее собственного кода она через конечное число шагов остановится, в противном
случае программа называется несамоприменимой. Пусть  —
множество кодов самоприменимых программ.
—
множество кодов самоприменимых программ.
Теорема.
Множество  алгоритмически неразрешимо.
алгоритмически неразрешимо.
Доказательство.
Пусть  — алгоритмически разрешимо. Тогда
существуют две программы
— алгоритмически разрешимо. Тогда
существуют две программы 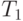 и
и  такие, что
такие, что 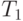 останавливается только на словах из
останавливается только на словах из  , а
, а  —
только на словах из
—
только на словах из  .
.
Тогда, если  на собственном коде остановится,
то
на собственном коде остановится,
то 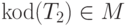 по определению
по определению  , но
, но  по
определению
по
определению  .
.
Если же  на своем коде не остановится, то по определению
на своем коде не остановится, то по определению 
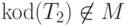 , а по определению
, а по определению 
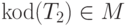 . Итак, в любом случае имеем противоречие.
. Итак, в любом случае имеем противоречие.
Еще одним примером алгоритмически неразрешимого множества является
множество  кодов программ, которые останавливаются при пустом
входе. Легко показать, что если бы
кодов программ, которые останавливаются при пустом
входе. Легко показать, что если бы  было разрешимым, то
множество
было разрешимым, то
множество  тоже было бы разрешимым.
тоже было бы разрешимым.

